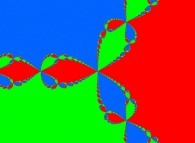
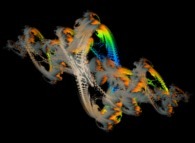
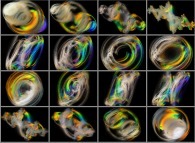
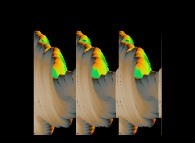
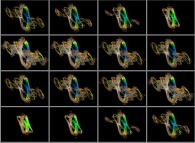
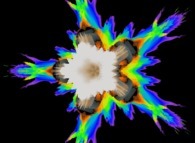
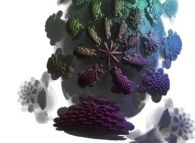
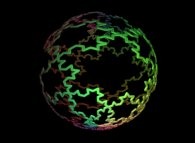
A foggy pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(0,1,0,0,0,0,0,0) -tridimensional cross-section-
[Un ensemble de Julia brumeux dans l'ensemble des pseudo-octonions (comme un 'MandelBulb': un 'JuliaBulb') calculé pour A=(0,1,0,0,0,0,0,0) -section tridimensionnelle-]. | 
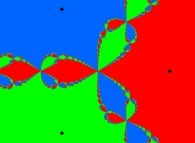
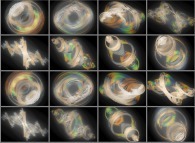
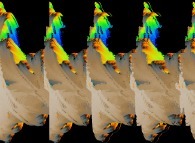
A foggy pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(-0.581514...,+0.635888...,0,0,0,0,0,0) -tridimensional cross-section-
[Un ensemble de Julia brumeux dans l'ensemble des pseudo-octonions (comme un 'MandelBulb': un 'JuliaBulb') calculé pour A=(-0.581514...,+0.635888...,0,0,0,0,0,0) -section tridimensionnelle-]. | 
A foggy pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(-0.581514...,+0.635888...,0,0,0,0,0,0) -tridimensional cross-section-
[Un ensemble de Julia brumeux dans l'ensemble des pseudo-octonions (comme un 'MandelBulb': un 'JuliaBulb') calculé pour A=(-0.581514...,+0.635888...,0,0,0,0,0,0) -section tridimensionnelle-]. | 
A foggy pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(-0.581514...,+0.635888...,0,0,0,0,0,0) -tridimensional cross-section-
[Un ensemble de Julia brumeux dans l'ensemble des pseudo-octonions (comme un 'MandelBulb': un 'JuliaBulb') calculé pour A=(-0.581514...,+0.635888...,0,0,0,0,0,0) -section tridimensionnelle-]. | 
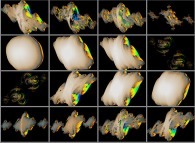
A foggy pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(-0.581514...,+0.635888...,0,0,0,0,0,0) and with a rotation about the X axis -tridimensional cross-section-
[Un ensemble de Julia brumeux dans l'ensemble des pseudo-octonions (comme un 'MandelBulb': un 'JuliaBulb') calculé pour A=(-0.581514...,+0.635888...,0,0,0,0,0,0) et avec une rotation autour de l'axe X -section tridimensionnelle-]. |

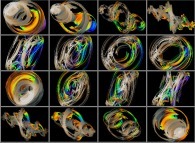
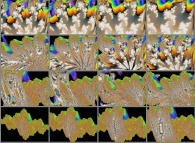
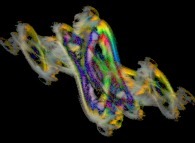
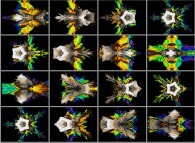
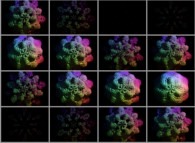
Zoom in on a pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(-0.581514...,+0.635888...,0,0,0,0,0,0) -tridimensional cross-section-
[Zoom sur un ensemble de Julia dans l'ensemble des pseudo-octonions (comme un 'MandelBulb': un 'JuliaBulb') calculé pour A=(-0.581514...,+0.635888...,0,0,0,0,0,0) et avec une rotation de 0 à pi autour de l'axe X -section tridimensionnelle-]. | 
Zoom in on a pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(-0.581514...,+0.635888...,0,0,0,0,0,0) with a (4xO+1)/(1xO-1) conformal transformation in the octonionic space -tridimensional cross-section-
[Zoom sur un ensemble de Julia dans l'ensemble des pseudo-octonions (comme un 'MandelBulb': un 'JuliaBulb') calculé pour A=(-0.581514...,+0.635888...,0,0,0,0,0,0) et avec une rotation de 0 à pi autour de l'axe X avec une transformation conforme (4xO+1)/(1xO-1) dans l'ensemble des octonions -section tridimensionnelle-]. | 
Zoom in on a pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(-0.581514...,+0.635888...,0,0,0,0,0,0) -tridimensional cross-section-
[Zoom sur un ensemble de Julia dans l'ensemble des pseudo-octonions (comme un 'MandelBulb': un 'JuliaBulb') calculé pour A=(-0.581514...,+0.635888...,0,0,0,0,0,0) et avec une rotation de 0 à pi autour de l'axe X -section tridimensionnelle-]. | 
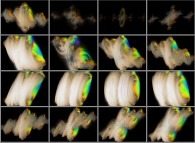
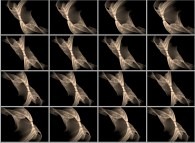
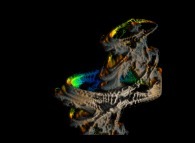
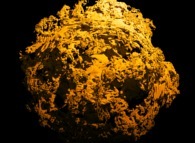
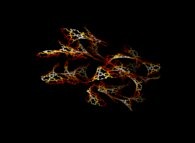
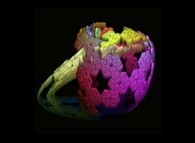
Close-up on a foggy pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(-0.581514...,+0.635888...,0,0,0,0,0,0) and with a rotation about the X axis -tridimensional cross-section-
[Agrandissement d'un ensemble de Julia brumeux dans l'ensemble des pseudo-octonions (comme un 'MandelBulb': un 'JuliaBulb') calculé pour A=(-0.581514...,+0.635888...,0,0,0,0,0,0) et avec une rotation autour de l'axe X -section tridimensionnelle-]. | 
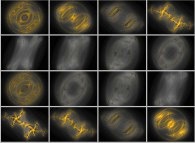
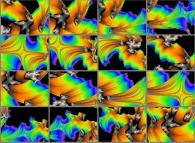
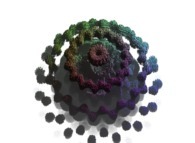
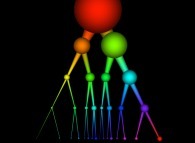
Pi/2 rotation about the X axis of a pseudo-quaternionic Julia set ('MandelBulb' like: a 'JuliaBulb') -tridimensional cross-section-
[Rotation de pi/2 autour de l'axe X d'un ensemble de Julia dans l'ensemble des pseudo-quaternions (comme un 'MandelBulb': un 'JuliaBulb') -section tridimensionnelle-]. |
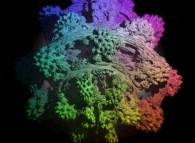
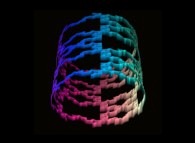
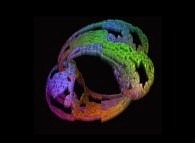
A foggy pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(-0.581514...,+0.635888...,0,0,0,0,0,0) and with a rotation about the X axis -tridimensional cross-section-
[Un ensemble de Julia brumeux dans l'ensemble des pseudo-octonions (comme un 'MandelBulb': un 'JuliaBulb') calculé pour A=(-0.581514...,+0.635888...,0,0,0,0,0,0) et avec une rotation autour de l'axe X -section tridimensionnelle-]. | 
Zoom in on a pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(-0.581514...,+0.635888...,0,0,0,0,0,0) -tridimensional cross-section-
[Zoom sur un ensemble de Julia dans l'ensemble des pseudo-octonions (comme un 'MandelBulb': un 'JuliaBulb') calculé pour A=(-0.581514...,+0.635888...,0,0,0,0,0,0) et avec une rotation de 0 à pi autour de l'axe X -section tridimensionnelle-]. | 
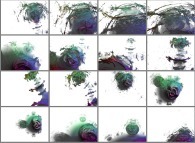
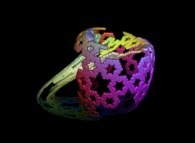
A foggy pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(-0.581514...,+0.635888...,0,0,0,0,0,0) and with a 0 to pi rotation about the X axis -tridimensional cross-section-
[Un ensemble de Julia brumeux dans l'ensemble des pseudo-octonions (comme un 'MandelBulb': un 'JuliaBulb') calculé pour A=(-0.581514...,+0.635888...,0,0,0,0,0,0) et avec une rotation de 0 à pi autour de l'axe X -section tridimensionnelle-]. | 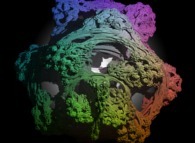
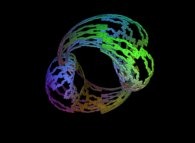
A foggy pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(-0.581514...,+0.635888...,0,0,0,0,0,0) and with a rotation about the X axis -tridimensional cross-section-
[Un ensemble de Julia brumeux dans l'ensemble des pseudo-octonions (comme un 'MandelBulb': un 'JuliaBulb') calculé pour A=(-0.581514...,+0.635888...,0,0,0,0,0,0) et avec une rotation autour de l'axe X -section tridimensionnelle-]. | 
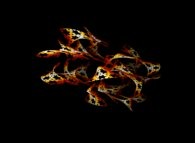
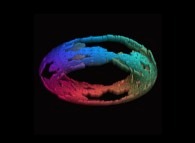
A foggy pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(-0.581514...,+0.635888...,0,0,0,0,0,0) -tridimensional cross-section-
[Un ensemble de Julia brumeux dans l'ensemble des pseudo-octonions (comme un 'MandelBulb': un 'JuliaBulb') calculé pour A=(-0.581514...,+0.635888...,0,0,0,0,0,0) -section tridimensionnelle-]. |

A foggy pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(-0.581514...,+0.635888...,0,0,0,0,0,0) -tridimensional cross-section-
[Un ensemble de Julia brumeux dans l'ensemble des pseudo-octonions (comme un 'MandelBulb': un 'JuliaBulb') calculé pour A=(-0.581514...,+0.635888...,0,0,0,0,0,0) -section tridimensionnelle-]. |
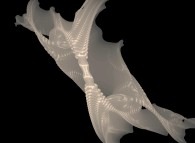

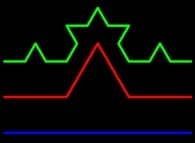

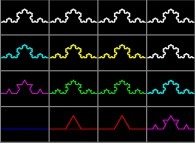

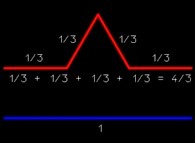
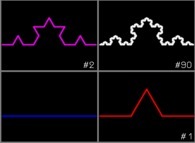
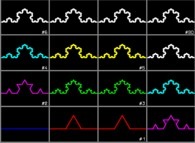
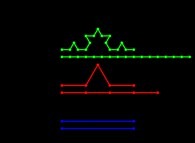
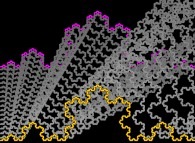

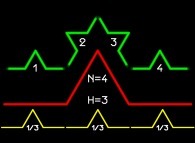
















































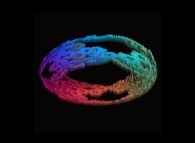


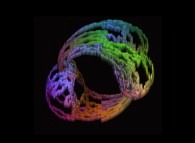









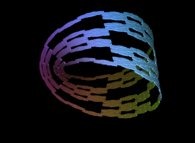


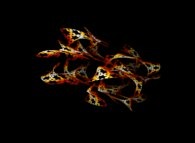















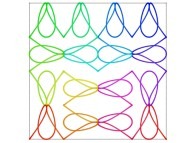
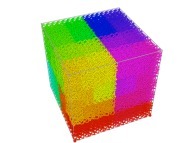
![The Bidimensional [0,1] --> [0,1]x[0,1] Peano Surjection -T defined with 2 digits- The Bidimensional [0,1] --> [0,1]x[0,1] Peano Surjection -T defined with 2 digits-](../images/PEAN.22.D/timbre.jpg)
![The Bidimensional [0,1] --> [0,1]x[0,1] Peano Surjection -T defined with 4 digits- The Bidimensional [0,1] --> [0,1]x[0,1] Peano Surjection -T defined with 4 digits-](../images/PEAN.24.D/timbre.jpg)
![The [0,1] --> [0,1]x[0,1] Peano Surjection -T defined with 6 digits- The [0,1] --> [0,1]x[0,1] Peano Surjection -T defined with 6 digits-](../images/PEAN.26.D/timbre.jpg)
![The Bidimensional [0,1] --> [0,1]x[0,1] Peano Surjection -T defined with 8 digits- The Bidimensional [0,1] --> [0,1]x[0,1] Peano Surjection -T defined with 8 digits-](../images/PEAN.28.D/timbre.jpg)




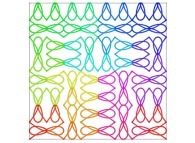


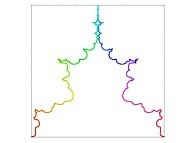
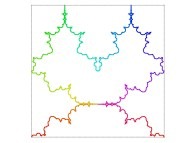
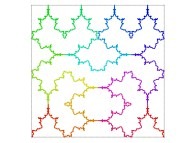
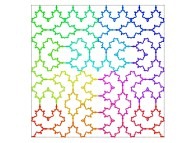
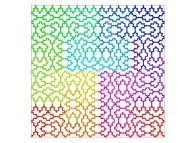


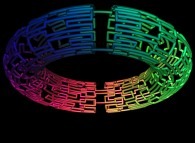


























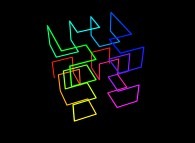
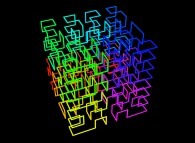

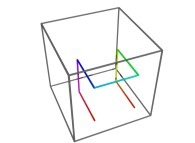
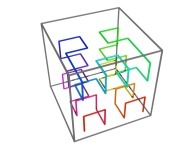
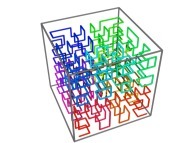


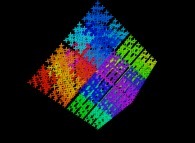
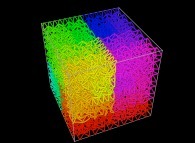
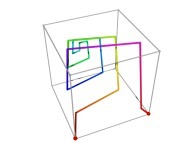
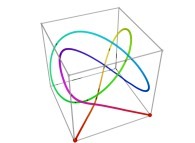
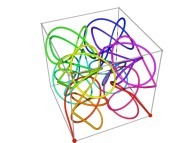
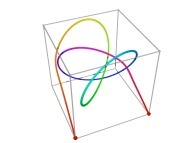
![The Tridimensional [0,1] --> [0,1]x[0,1]x[0,1] Peano Surjection -T defined with 3 digits- The Tridimensional [0,1] --> [0,1]x[0,1]x[0,1] Peano Surjection -T defined with 3 digits-](../images/PEAN.12.D/timbre.jpg)
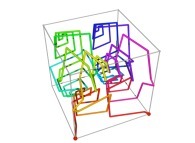
![The Tridimensional [0,1] --> [0,1]x[0,1]x[0,1] Peano Surjection -T defined with 6 digits- The Tridimensional [0,1] --> [0,1]x[0,1]x[0,1] Peano Surjection -T defined with 6 digits-](../images/PEAN.13.D/timbre.jpg)
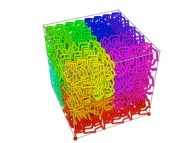
![The Tridimensional [0,1] --> [0,1]x[0,1]x[0,1] Peano Surjection -T defined with 9 digits- The Tridimensional [0,1] --> [0,1]x[0,1]x[0,1] Peano Surjection -T defined with 9 digits-](../images/PEAN.14.D/timbre.jpg)
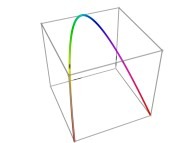
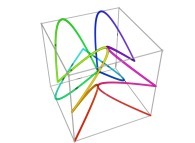
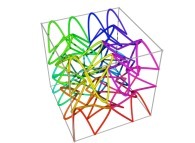










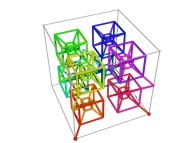
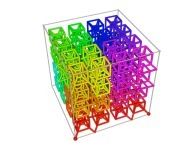

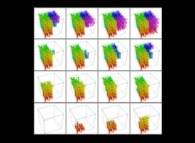
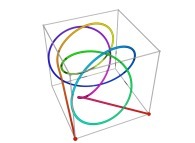
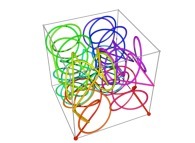



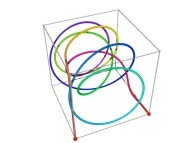
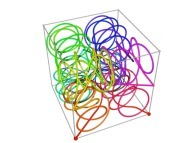
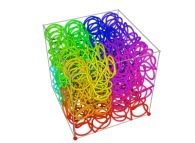




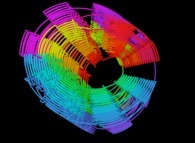
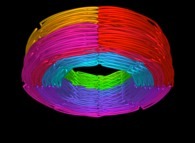













































































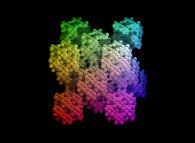


























































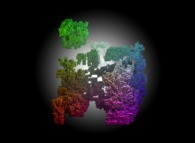



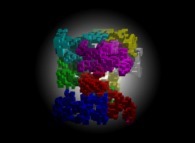
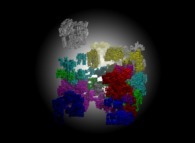
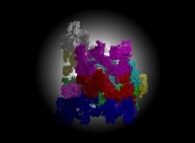


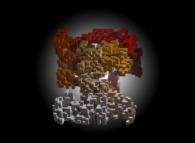




















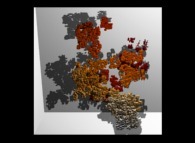

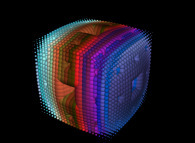





























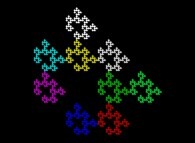
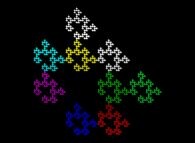






















































































































































































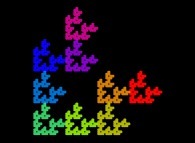
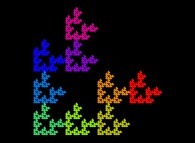











































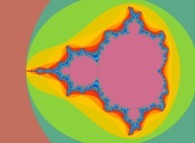

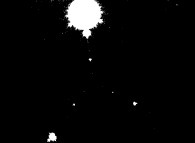






























![Tridimensional display of the Z=Gamma(Z) iteration inside [-20.0,+20.0]x[-20.0,+20.0] (bird's-eye view) Tridimensional display of the Z=Gamma(Z)iteration inside [-20.0,+20.0]x[-20.0,+20.0] (bird's-eye view)](../images/ITGA.11.m.D/timbre.jpg)
![Tridimensional display of the Z=Gamma(Z) iteration inside [-20.0,+20.0]x[-20.0,+20.0] Tridimensional display of the Z=Gamma(Z)iteration inside [-20.0,+20.0]x[-20.0,+20.0]](../images/ITGA.11.M.D/timbre.jpg)

![Tridimensional display of the Z=Zeta(Z) iteration inside [-20.0,+20.0]x[-20.0,+20.0] (bird's-eye view) Tridimensional display of the Z=Zeta(Z)iteration inside [-20.0,+20.0]x[-20.0,+20.0] (bird's-eye view)](../images/ITZE.11.m.D/timbre.jpg)
![Tridimensional display of the Z=Zeta(Z) iteration inside [-20.0,+20.0]x[-20.0,+20.0] Tridimensional display of the Z=Zeta(Z)iteration inside [-20.0,+20.0]x[-20.0,+20.0]](../images/ITZE.11.M.D/timbre.jpg)