![About the length of the von Koch curve [A propos de la longueur de la courbe de von Koch ] About the length of the von Koch curve [A propos de la longueur de la courbe de von Koch ]](image.jpg)
About the length of the von Koch curve [A propos de la longueur de la courbe de von Koch].
See some related pictures:
90
| 4 |
|---| = 175.584.548.321 > 150.000.000.000 meters Earth-Sun mean distance
| 3 |
103
| 4 |
|---| = 7.390.773.120.492 > 7.375.000.000.000 meters Pluto-Sun maximal distance
| 3 |
216
| 4 |
|---| = 969.989.665.898.299.409.932.022.080 > 879.245.710.860.384.000.000.000.000 meters diameter of the observable universe (~93 billions of light-years)
| 3 |
Du continu différentiable au continu non différentiable:
Au milieu du dix-neuvième
siècle, sous l'impulsion de Weierstrass, Cantor, Peano,
Lebesgue, Hausdorff, Besicovitch, von Koch, Sierpinski,...
apparurent des objets pestiférés (selon les termes de Charles Hermite) et en
particulier d'incroyables "courbes" qui bien que continues, n'étaient
pas différentiables. Personne alors n'en vit alors l'intérêt "pratique" et il
fallut attendre la deuxième moitié du vingtième siècle pour que Benoît
Mandelbrot nous révèle leur richesse en offrant aux Mathématiciens,
aux physiciens et à bien d'autres, une nouvelle géométrie: celle
des objets fractals.
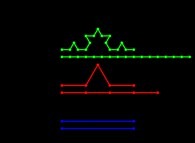
Le plus simple d'entre-eux est bien certainement la courbe de
von Koch. Comme la plupart de ces objets, elle est définie par une règle
de construction répétée indéfiniment qui, dans son cas, consiste
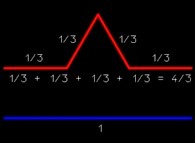
à remplacer un segment par un ensemble de N=4 segments R=3 fois plus petits
et formant une sorte de pic (ainsi le segment bleu est transformé en l'ensemble rouge
-#1- sur la figure).
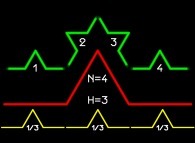
A partir du nombre de copies N et du rapport d'homothétie R,
une mesure de la "rugosité", de l'irrégularité est définie: c'est la
dimension fractale D égale à log(N)/log(R) et qui n'est donc pas, en général,
un nombre entier (sauf évidemment si l'objet n'est pas fractal: par exemple, dans le cas d'un
cube de côté C, D est égale à log(C^3)/log(C)=3).
Pour la courbe de von Koch elle vaut donc D=log(4)/log(3)=1,26...; cette courbe est donc "comprise" entre une droite (D=1) et un plan (D=2).
Deux caractéristiques fondamentales des objets fractals apparaissent
de façon évidente ici: d'une part l'autosimilarité (des structures de même
forme apparaissent à toutes les échelles) et d'autre part ils possèdent
à la fois des propriétés finies et infinies (dans le cas de la courbe de
von Koch, son domaine est évidemment limité, alors que sa longueur
ne l'est pas: celle-ci croit d'ailleurs incroyablement vite et par exemple, si
le segment bleu mesure un mètre, à l'itération #90 la courbe mesure
(4/3)^90 mètres, soit une longueur supérieure à la distance moyenne de la
Terre au Soleil!). Et nombreux sont les objets de la nature possédant ces caractéristiques
: une branche de chêne ressemble à un chêne; la surface des alvéoles pulmonaires,
qui résident dans une petite partie du faible volume de la cage thoracique,
est de l'ordre de la centaine de mètres carrés.
(CMAP28 WWW site: this page was created on 02/09/2018 and last updated on 01/22/2025 12:05:55 -CET-)
[See the generator of this picture [Voir le générateur de cette image]]
[See all related pictures (including this one) [Voir toutes les images associées (incluant celle-ci)]]
[Please visit the related DeterministicFractalGeometry picture gallery [Visitez la galerie d'images DeterministicFractalGeometry associée]]
[Please visit the related ImagesDidactiques picture gallery [Visitez la galerie d'images ImagesDidactiques associée]]
[Go back to AVirtualMachineForExploringSpaceTimeAndBeyond [Retour à AVirtualMachineForExploringSpaceTimeAndBeyond]]
[The Y2K Bug [Le bug de l'an 2000]]
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[Mail [Courrier]]
[About Pictures and Animations [A Propos des Images et des Animations]]
Copyright © Jean-François COLONNA, 2018-2025.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2018-2025.
![About the length of the von Koch curve [A propos de la longueur de la courbe de von Koch ] About the length of the von Koch curve [A propos de la longueur de la courbe de von Koch ]](image.jpg)
![About the length of the von Koch curve [A propos de la longueur de la courbe de von Koch ] About the length of the von Koch curve [A propos de la longueur de la courbe de von Koch ]](image.jpg)


