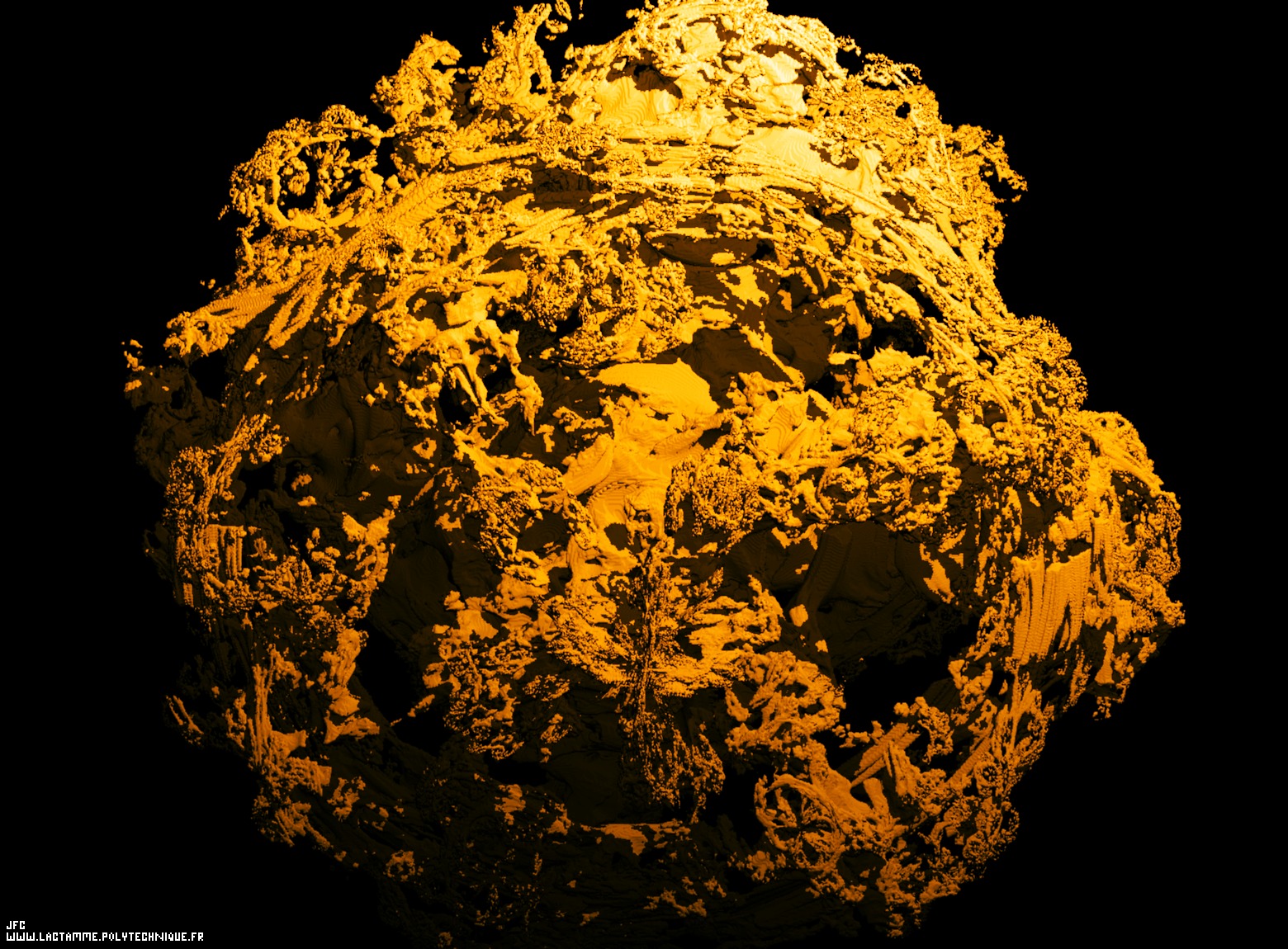
A pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(-0.581514...,+0.635888...,0,0,0,0,0,0) and with a locally variable exponent that is equal to 4, 5 or 6 and with a rotation about the X axis -tridimensional cross-section- [Un ensemble de Julia dans l'ensemble des pseudo-octonions (comme un 'MandelBulb': un 'JuliaBulb') calculé pour A=(-0.581514...,+0.635888...,0,0,0,0,0,0) et avec un exposant variable localement valant 4, 5 ou 6 et avec une rotation autour de l'axe X -section tridimensionnelle-].

                    
                    P(o) = 1*o + {-0.5815147625160462,+0.6358885017421603,0,0,0,0,0,0}

                    
                                       E
                    fR(R ,R ) = (R *R )
                        1  2      1  2

                    
                    fA1(A1 ,A1 ) = E*(A1 +A1 )
                          1   2         1   2

                    
                    fA2(A2 ,A2 ) = E*(A2 +A2 )
                          1   2         1   2

                    
                    fA3(A3 ,A3 ) = E*(A3 +A3 )
                          1   2         1   2

                    
                    fA4(A4 ,A4 ) = E*(A4 +A4 )
                          1   2         1   2

                    
                    fA5(A5 ,A5 ) = E*(A5 +A5 )
                          1   2         1   2

                    
                    fA6(A6 ,A6 ) = E*(A6 +A6 )
                          1   2         1   2

                    
                    fA7(A7 ,A7 ) = E*(A7 +A7 )
                          1   2         1   2

                    
                    ∈ = IntegerPart(FractalFunction(x,y,z,...) ∈ [4,6])