
A periodical tiling of the plane using 3 von Koch-like snowflakes -iteration 3- [Un pavage périodique du plan utilisant 3 flocons de neige de type von Koch -itération 3-].

A periodical tiling of the plane using 3 von Koch-like snowflakes -iteration 3- [Un pavage périodique du plan utilisant 3 flocons de neige de type von Koch -itération 3-].
 2 snowflakes 3 iterations. |  3 snowflakes 3 iterations. |  4 snowflakes 3 iterations. |
 2 snowflakes 3 iterations. |  3 snowflakes 3 iterations. |  4 snowflakes 3 iterations. |
 2 snowflakes 3 iterations. | 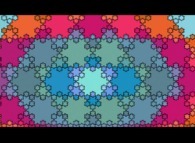 3 snowflakes 3 iterations. |  4 snowflakes 3 iterations. |
 2 snowflakes 2 iterations. |  2 snowflakes 3 iterations. |  2 snowflakes 4 iterations. |  2 snowflakes 5 iterations. |
 2 snowflakes 2 iterations. |  2 snowflakes 3 iterations. |  2 snowflakes 4 iterations. |  2 snowflakes 5 iterations. |
 |  |  |  2 snowflakes 5 iterations. |
 3 snowflakes 2 iterations. |  3 snowflakes 3 iterations. |  3 snowflakes 4 iterations. |  3 snowflakes 5 iterations. |
 3 snowflakes 2 iterations. |  3 snowflakes 3 iterations. |  3 snowflakes 4 iterations. |  3 snowflakes 5 iterations. |
 |  |  |  3 snowflakes 5 iterations. |
 2 snowflakes 3 iterations. |  3 snowflakes 3 iterations. |  4 snowflakes 3 iterations. |
 2 snowflakes 3 iterations. |  3 snowflakes 3 iterations. |  4 snowflakes 3 iterations. |
 2 snowflakes 3 iterations. | 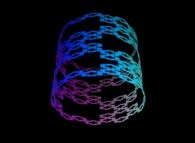 3 snowflakes 3 iterations. |  4 snowflakes 3 iterations. |
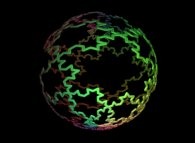 2 snowflakes 3 iterations. |  3 snowflakes 3 iterations. |  4 snowflakes 3 iterations. |
 2 snowflakes 3 iterations. |  3 snowflakes 3 iterations. |  4 snowflakes 3 iterations. |
 2 snowflakes 3 iterations. |  3 snowflakes 3 iterations. | 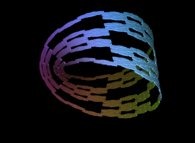 4 snowflakes 3 iterations. |
 2 snowflakes 3 iterations. |  3 snowflakes 3 iterations. |  4 snowflakes 3 iterations. |
 2 snowflakes 3 iterations. |  3 snowflakes 3 iterations. |  4 snowflakes 3 iterations. |
 2 snowflakes 3 iterations. |  3 snowflakes 3 iterations. | 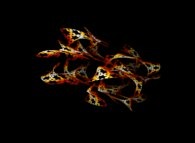 4 snowflakes 3 iterations. |