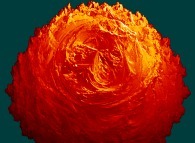
Sixteen pseudo-quaternionic Julia sets ('MandelBulb' like: 'JuliaBulb's) -tridimensional cross-sections- [Seize ensembles de Julia dans l'ensemble des pseudo-quaternions (comme un 'MandelBulb': des 'JuliaBulb's) -coupes tridimensionnelles-]
.
Sixteen pseudo-quaternionic Julia sets ('MandelBulb' like: 'JuliaBulb's) -tridimensional cross-sections- [Seize ensembles de Julia dans l'ensemble des pseudo-quaternions (comme un 'MandelBulb': des 'JuliaBulb's) -coupes tridimensionnelles-]
. 2
P(q) = q + {X ,Y ,0,0}
A A
fR(R ,R ) = R *R
1 2 1 2
fT(T ,T ) = T +T
1 2 1 2
fP(P ,P ) = P +P
1 2 1 2
fA(A ,A ) = A +A
1 2 1 2
the point {XA,YA} following an Archimedes spiral located in the complex plane and with the origin of the coordinates as its center.
