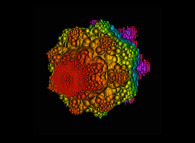
A pseudo-octonionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- [Un ensemble de Mandelbrot dans l'ensemble des pseudo-octonions (un 'MandelBulb') -section tridimensionnelle- ]

A pseudo-octonionic Mandelbrot set (a 'MandelBulb') -tridimensional cross-section- [Un ensemble de Mandelbrot dans l'ensemble des pseudo-octonions (un 'MandelBulb') -section tridimensionnelle-].




This Mandelbrot set is a tridimensional cross-section and was computed with a polynomial 'P' of the first degree ('C' denoting the current octonionic point) and the following eight functions: 
                    
                    P(o) = 1*o + C

                    
                                       8
                    fR(R ,R ) = (R *R )
                        1  2      1  2

                    
                    fA1(A1 ,A1 ) = 8*(A1 +A1 )
                          1   2         1   2

                    
                    fA2(A2 ,A2 ) = 8*(A2 +A2 )
                          1   2         1   2

                    
                    fA3(A3 ,A3 ) = 8*(A3 +A3 )
                          1   2         1   2

                    
                    fA4(A4 ,A4 ) = 1*(A4 +A4 )
                          1   2         1   2

                    
                    fA5(A5 ,A5 ) = 1*(A5 +A5 )
                          1   2         1   2

                    
                    fA6(A6 ,A6 ) = 1*(A6 +A6 )
                          1   2         1   2

                    
                    fA7(A7 ,A7 ) = 1*(A7 +A7 )
                          1   2         1   2



See another cross-section:

A pseudo-octonionic Mandelbrot set (a 'MandelBulb')-'children's corner' or 'the consciousness emerging from Mathematics'- -tridimensional cross-section-



See the zoom in on the pseudo-octonionic Mandelbrot set:

Zoom in on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')-tridimensional cross-section-



See some close-ups possibly including this one:

A pseudo-octonionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')-tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')-tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')-tridimensional cross-section-

A pseudo-octonionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')-tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')-tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')-tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')-tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')-tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')-tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')-tridimensional cross-section-

A pseudo-octonionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')-tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')-tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')-tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')-tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')-tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')-tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')-tridimensional cross-section-
A pseudo-octonionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')-tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')-tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')-tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')-tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')-tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')-tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')-tridimensional cross-section-



See some conformal transformations in the pseudo-octonionic space:

A pseudo-octonionic Mandelbrot set (a 'Mandelbulb')with a 1/O conformal transformation in the pseudo-octonionic space -tridimensional cross-section- A pseudo-octonionic Mandelbrot set (a 'Mandelbulb')with a O^2 conformal transformation in the pseudo-octonionic space -tridimensional cross-section- A pseudo-octonionic Mandelbrot set (a 'Mandelbulb')with a (4xO+1)/(1xO-1) conformal transformation in the pseudo-octonionic space -tridimensional cross-section-  
A pseudo-octonionic Mandelbrot set (a 'Mandelbulb')with a 1/O conformal transformation in the pseudo-octonionic space -tridimensional cross-section- A pseudo-octonionic Mandelbrot set (a 'Mandelbulb')with a O^2 conformal transformation in the pseudo-octonionic space -tridimensional cross-section- A pseudo-octonionic Mandelbrot set (a 'Mandelbulb')with a (4xO+1)/(1xO-1) conformal transformation in the pseudo-octonionic space -tridimensional cross-section-  
Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')with a 1/O conformal transformation in the pseudo-octonionic space -tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')with a O^2 conformal transformation in the pseudo-octonionic space -tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')with a (4xO+1)/(1xO-1) conformal transformation in the pseudo-octonionic space -tridimensional cross-section-  
Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')with a 1/O conformal transformation in the pseudo-octonionic space -tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')with a O^2 conformal transformation in the pseudo-octonionic space -tridimensional cross-section- Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb')with a (4xO+1)/(1xO-1) conformal transformation in the pseudo-octonionic space -tridimensional cross-section-



[for more information about pseudo-quaternionic numbers (en français/in french)]
[for more information about pseudo-octionic numbers (en français/in french)]

[for more information about N-Dimensional Deterministic Fractal Sets (in english/en anglais)]
[Plus d'informations à propos des Ensembles Fractals Déterministes N-Dimensionnels (en français/in french)]


See an artistic variation:

Untitled 0597


See some related pictures (including this one) about picture sharpening:

A pseudo-octonionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- A pseudo-octonionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section, picture sharpening- A pseudo-octonionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section, picture sharpening-


(CMAP28 WWW site: this page was created on 01/01/2012 and last updated on 06/04/2026 22:49:56 -CEST-)



[See the generator of this picture [Voir le générateur de cette image]]

[See all related pictures (including this one) [Voir toutes les images associées (incluant celle-ci)]]

[See the following comment(s): octonionic numbers, pseudo-octonionic numbers, Mandelbrot set [Voir le(s) commentaire(s) suivant(s): octonions, pseudo-octonions, ensemble de Mandelbrot]]
[Please visit the related DeterministicFractalGeometry picture gallery [Visitez la galerie d'images DeterministicFractalGeometry associée]]
[Please visit the related GeneralitiesVisualization picture gallery [Visitez la galerie d'images GeneralitiesVisualization associée]]
[Please visit the related ImagesDesMathematiques picture gallery [Visitez la galerie d'images ImagesDesMathematiques associée]]

[Go back toMathematics - A Virtual Instrument For Exploring Space Time And Beyond [Retour à {a chapter of 'Mathematics-AVirtualInstrumentForExploringSpaceTimeAndBeyond'}]]

[The Y2K Bug [Le bug de l'an 2000]]
[Are we ready for the Year 2038 [Notre informatique est-elle prête pour l'An 2038]?]

[Site Map and Help [Plan du Site et Aide]]
[Mail [Courrier]]
[About Pictures and Animations [A Propos des Images et des Animations]]


Copyright © Jean-François COLONNA, 2012-2026.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2012-2026.