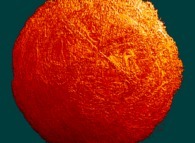
2.pi rotation about the Y axis of a pseudo-quaternionic Julia set ('MandelBulb' like: a 'JuliaBulb') -tridimensional cross-section- [Rotation de 2.pi autour de l'axe Y d'un ensemble de Julia dans l'ensemble des pseudo-quaternions (comme un 'MandelBulb': un 'JuliaBulb') -section tridimensionnelle-].

                                  2
                    P(q) = 1*q + q + {-0.5815147625160462,+0.6358885017421603,0,0}

                                       2
                    fR(R ,R ) = (R *R )
                        1  2      1  2

                    fT(T ,T ) = 2*(T +T )
                        1  2        1  2

                    fP(P ,P ) = 2*(P +P )
                        1  2        1  2

                    fA(A ,A ) = 2*(A +A )
                        1  2        1  2