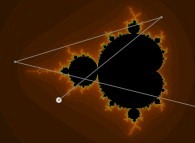
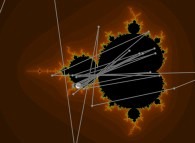
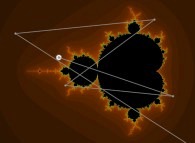
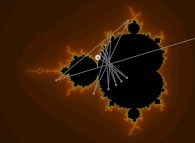
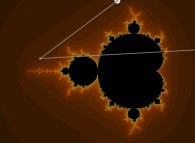
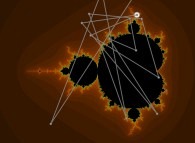
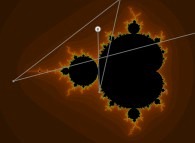
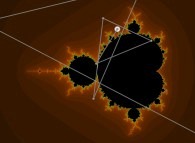
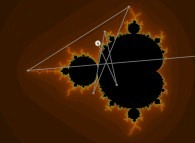
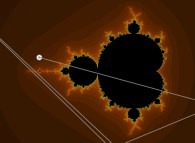
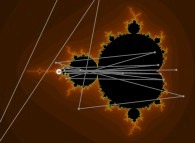
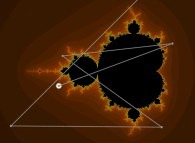
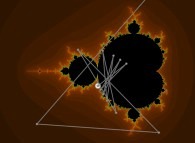
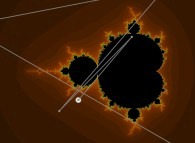
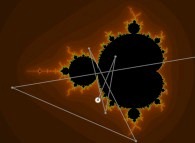
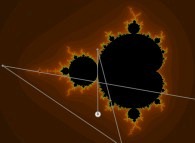
Iterations in the complex plane: the computation of the Mandelbrot set [Itérations dans le plan complexe: le calcul de l'ensemble de Mandelbrot].

Iterations in the complex plane: the computation of the Mandelbrot set [Itérations dans le plan complexe: le calcul de l'ensemble de Mandelbrot].
Z = 0
0
2
Z = Z + C
n+1 n
where 'C' denotes the current point.