A Quoi Servent et Que Sont les Mathématiques ?
CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[Real Numbers don't exist in Computers and Floating Point Computations aren't safe. [Les Nombres Réels n'existent pas dans les Ordinateurs et les Calculs Flottants ne sont pas sûrs.]]
[N'oubliez pas de visiter Une Machine Virtuelle à Explorer l'Espace-Temps et au-delà où vous trouverez plus de 10.000 images et animations à la frontière de l'Art et de la Science]
(Site WWW CMAP28 : cette page a été créée le 10/03/2013 et mise à jour le 02/02/2026 10:52:30 -CET-)
[voir la version "arborescente" du plan de cette page]
Résumé :
Souvent considérées comme inutiles, les Mathématiques, sans que nous en ayons toujours conscience, sont omniprésentes dans la vie courante
(diodes électro-luminescentes,
téléphone portable,
photographie numérique,
GPS,
Intelligence Artificielle,...).
Mais elles sont surtout le Langage de la Science et de l'Industrie
et leur redoutable efficacité dans ce domaine est peut-être un révélateur de leur nature profonde.
Aujourd'hui, puissamment secondées par les ordinateurs, elles peuvent aussi être considérées, à côté du
microscope et du télescope, comme un
instrument d'optique virtuel qui chaque jour nous dévoile de nouveaux et
mystérieux aspects de notre Univers -y compris nous-mêmes- et au-delà...
Mots-Clefs :
Anaglyphes,
Art et Science,
Autostéréogrammes,
Chaos Déterministe,
Création Artistique,
Entrelacs,
Erreurs d'arrondi,
Expérimentation Virtuelle,
Génie Logiciel,
Géométrie Fractale,
Infographie,
Mathématiques,
Mécanique Céleste,
Mécanique Quantique,
Physique,
Sensibilité aux Erreurs d'Arrondi,
Simulation Numérique,
Stéréogrammes,
Synthèse de Phénomènes Naturels,
Synthèse de Texture,
Visualisation Scientifique,
Voyage Virtuel dans l'Espace-Temps.
1-LES MATHEMATIQUES PURES, UN "SIMPLE" (ET INUTILE ?) JEU DE L'ESPRIT :
Pour commencer, nous définirons les Mathématiques comme un ensemble de symboles abstraits, de règles de
manipulation et d'axiomes (c'est-à-dire des vérités de "base" admises par tous, pour leur évidence a priori ou a posteriori)
à partir desquels seront démontrés des théorèmes (c'est-à-dire de nouveaux énoncés vrais)
en suivant un chemin logique incontestable et vérifiable.
Et face à une conjecture (on appelle ainsi un théorème non encore démontré, qui "résiste" et
dont on pense qu'il est vrai, se rappelant qu'il est toujours
possible de se tromper !), le travail du mathématicien consistera à en trouver une démonstration...
Au jeu d'échec, à côté des parties que l'on peut jouer contre un adversaire (homme ou machine...),
il est fréquent, partant d'une certaine configuration de pièces sur l'échiquier,
de se poser le problème suivant : comment faire mat en le moins de coups possibles ? Le résoudre n'apporte, en général,
qu'une satisfaction intellectuelle.
Il en est de même en Mathématiques : elles puisent leur inspiration dans des problèmes bien souvent
déconnectés du "réel" et dont l'utilité n'est pas évidente, ni a priori, ni a posteriori.
En voici quelques exemples choisis parmi les plus "élémentaires" (à formuler...) et qui sont dits ouverts car non
encore résolus :
- En 1928, Lothar Collatz formule la conjecture de Syracuse (du nom de l'Université américaine).
Partant d'un entier N quelconque, la suite suivante est définie :
U = N
0
si U est pair :
n
U
n
U = ----
n+1 2
sinon :
U = 3.U + 1
n+1 n
Là aussi, toutes les expériences faites à l'aide d'ordinateurs
montrent que tôt ou tard, quel que soit le nombre N de départ, le processus tombe sur la valeur 1,
puis sur la séquence {4,2,1} indéfiniment répétée. Mais est-ce vrai pour tout N ?
- Il y a une infinité de nombres entiers. Il y a une infinité de nombres premiers
et cela est connu depuis plus de deux millénaires. En observant la liste des premiers d'entre-eux,
on observe qu'il existe des nombres premiers dits jumeaux c'est-à-dire
des couples {P1,P2} tels que |P1-P2|=2 :
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41,...
|__|__| |____| |____| |____|
Aujourd'hui, cette observation se fait à l'aide d'ordinateurs. Mais ces machines sont incapables de répondre
à la question de savoir s'il y en a une infinité puisque elles ne permettent que d'étudier un nombre fini de cas !
- Au milieu du XVIIIe siècle, Christian Goldbach et Leonhard Euler énonçaient la conjecture suivante :
tout nombre pair strictement supérieur à 2 serait, au moins d'une façon, la somme de deux nombres premiers. Ainsi :
4 = 2+2
6 = 3+3
8 = 3+5 [= 5+3]
10 = 3+7 = 5+5 [= 7+3]
(...)
990 = 7+983 = 13+977 = 19+971 = 23+967 = 37+953 = 43+947 = 53+937 = 61+929 = 71+919 = 79+911
= 83+907 = 103+887 = 107+883 = 109+881 = 113+877 = 127+863 = 131+859 = 137+853 = 151+839 = 163+827
= 167+823 = 179+811 = 181+809 = 193+797 = 229+761 = 233+757 = 239+751 = 251+739 = 257+733 = 263+727
= 271+719 = 281+709 = 307+683 = 313+677 = 317+673 = 331+659 = 337+653 = 347+643 = 349+641 = 359+631
= 373+617 = 383+607 = 389+601 = 397+593 = 419+571 = 421+569 = 433+557 = 443+547 = 449+541 = 467+523
= 487+503 = 491+499
[= 499+491 = 503+487 = 523+467 = 541+449 = 547+443 = 557+433 = 569+421 = 571+419 = 593+397 = 601+389
= 607+383 = 617+373 = 631+359 = 641+349 = 643+347 = 653+337 = 659+331 = 673+317 = 677+313 = 683+307
= 709+281 = 719+271 = 727+263 = 733+257 = 739+251 = 751+239 = 757+233 = 761+229 = 797+193 = 809+181
= 811+179 = 823+167 = 827+163 = 839+151 = 853+137 = 859+131 = 863+127 = 877+113 = 881+109 = 883+107
= 887+103 = 907+83 = 911+79 = 919+71 = 929+61 = 937+53 = 947+43 = 953+37 = 967+23 = 971+19
= 977+13 = 983+7]
(...)
La remarque formulée précédemment concernant les ordinateurs est encore valable ici, mais à une petite
différence importante près. En effet, une telle recherche informatique pourrait amener à découvrir un
contre-exemple (c'est-à-dire nous révéler un nombre pair non décomposable), ce qui n'a pas
de sens pour les nombres premiers jumeaux (ne plus en observer à partir du nombre N ne prouve pas que cela
se maintient jusqu'à l'infini...). Ainsi, dans le cas de la conjecture de Goldbach, l'ordinateur
pourrait nous montrer qu'elle est fausse...
Mais tous les problèmes ouverts aujourd'hui ne sont pas aussi simples à formuler.
En août 1900, au cours du second Congrès International des Mathématiciens à Paris,
David Hilbert dressait une liste de vingt-trois problèmes qu'il considérait comme les plus importants et
les plus stimulants pour la recherche. Aujourd'hui plusieurs d'entre-eux ne sont toujours pas résolus et
par exemple :
- L'hypothèse de Riemann (1859) liée étroitement à la distribution des nombres premiers
et qui prétend que les zéros non triviaux de la fonction Zeta ont tous une partie réelle égale à 1/2.
- L'Hypothèse du Continu (HC) formulée par Georg Cantor à la fin du XIXe siècle : elle
affirme qu'il n'y a pas de cardinaux entre celui des entiers et celui des réels [01].
Il existe, malgré tout de rares exceptions à cette nature abstraite des grands problèmes. C'est ainsi que la Fondation Clay a dressé en l'an 2000
la liste des sept problèmes du millénaire (récompensés chacun par un prix d'un million de dollars)
et parmi lesquels figure l'étude des équations de Navier-Stokes
qui concernent très directement la Mécanique des fluides et donc des applications industrielles (aéronautique, météorologie,...).
Ces quelques exemples pourraient donc conforter l'idée que les Mathématiques ne sont qu'un inutile jeu de l'esprit.
A l'aide d'un cas historique, montrons qu'il n'en est rien.
Le théorème de Pythagore est connu et démontré depuis plus de 2500 ans.
Remarquons au passage qu'il y a un peu de magie dans une démonstration : en effet, en procédant ainsi, une infinité de cas sont traités simultanément.
Le théorème de Pythagore qui affirme que "dans tout triangle rectangle, le carré de l'hypoténuse est égal à la somme des
carrés des deux autres côtés" [02] porte sur tous les triangles rectangles de la géométrie euclidienne,
quelles que soient leurs proportions ou leurs tailles et ce alors que sa vérification est en toute rigueur impossible, en particulier de par le
nombre infini de ces triangles [03], mais aussi à cause du fait que des mesures de longueur infiniment précises sont interdites par la Physique !
En notant X, Y et Z les deux côtés de l'angle droit et l'hypoténuse respectivement, le théorème de Pythagore peut s'écrire :
2 2 2
Z = X + Y
Partant de cette formule à quoi peut-on jouer ? Par exemple, considérer que cette relation est une équation à trois
variables {X,Y,Z} et n'en chercher que les solutions entières. Ainsi, au II et IIIe siècle de notre ère
vivait à Alexandrie le mathématicien Diophante qui se posait ce genre de problème (appelé aujourd'hui étude des équations
diophantiennes en son honneur). Une partie de ses travaux, traduite
du grec en latin au XVIIe siècle par Claude Gaspard Bachet de Méziriac, tombèrent entre les mains de Pierre de Fermat,
magistrat au parlement provincial de Toulouse et mathématicien et physicien "amateur" de génie.
L'équation précédente possède une infinité de solutions et par exemple la plus fameuse d'entre-elles :
2 2 2
3 + 4 = 5
ou encore :
2 2 2
5 + 12 = 13
2 2 2
8 + 15 = 17
(...)
Pierre de Fermat eut l'idé de généraliser cette équation de la façon suivante :
n n n
X + Y = Z {X,Y,Z,n} ∈ N X.Y.Z # 0
et l'intuition qu'elle ne possédait pas de solutions entières {X,Y,Z} pour n>2 (ainsi que pour n=0 évidemment).
Il crut l'avoir démontré comme l'atteste son annotation manuscrite dans la marge de son ouvrage, mais n'en ayant
retrouvé aucune trace [04],
il parait évident aujourd'hui qu'il avait commis une erreur et s'en était certainement
rendu compte rapidement.
Ce qui fut appelé "Grand Théorème de Fermat" (par abus de langage, puisqu'il ne s'agissait en
fait que d'une conjecture) est resté dans l'histoire des Mathématiques : beaucoup de grands noms s'y sont "frottés"
avec plus ou moins de succès (toujours partiels...) et il fallu attendre 1994 pour que Andrew Wiles [05] achève l'œuvre
de ses prédécesseurs : trois siècles et demi d'efforts !
Or ce théorème n'a que peu d'utilité pratique [06] et cela pourrait donc encore conforter l'idée de l'inutilité des Mathématiques !
Mais évidemment il n'en est rien. En effet, d'une part le chemin parcouru au cours des siècles pour sa démonstration
fut des plus enrichissant en établissant des ponts entre des domaines antérieurement disjoints. D'autre part,
certaines applications concrètes ont vu le jour : c'est ainsi le cas des courbes dites elliptiques, essentielles
pour arriver au résultat, et qui sont utilisées aujourd'hui en cryptographie...
2-LES MATHEMATIQUES APPLIQUEES, DE L'INDUSTRIE A LA RECHERCHE LA PLUS FONDAMENTALE :
2.1-LE PHYSICIEN, OBSERVATEUR ET ARPENTEUR DE L'UNIVERS :
En premier lieu, rappelons que la tâche première du physicien est de regarder, d'observer ce qui l'entoure, prés ou loin de lui.
Le sens de la vision joue ici un rôle essentiel et il est d'ailleurs très certainement
à l'origine de la curiosité scientifique en nous permettant de constater des régularités, des symétries, des invariances,... "autour" de nous.
D'ailleurs que serait notre conception de la Réalité sans nos yeux ?
En second lieu, le physicien mesure (des longueurs, des vitesses, des températures,...).
On notera qu'aujourd'hui, qu'il s'agisse d'observation ou de mesure, il est rare, en ce qui
concerne la physique fondamentale, que ces opérations puissent être menées sans un appareillage
tout à la fois très complexe et fort coûteux. A titre d'exemple l'étude expérimentale des particules élémentaires se
fait à l'aide d'accélérateurs de particules tel le LHC (Large Hadron Collider) du CERN à Genève.
Cette "machine" est à l'intérieur d'un tunnel de 27 kilomètres de circonférence et les "outils de mesure"
pèsent de l'ordre de 10.000 tonnes chacun [07]. Il en est de même
à l'autre bout de l'échelle et l'on peut imaginer sans trop de peine la difficulté de mesurer, par exemple, la
distance des galaxies lointaines.
Montrons en quelques images (nées des Mathématiques comme cela sera détaillé par la suite) ce que décrit la Physique aujourd'hui :
+26
8.8 10 mètres
 |  | Les étoiles et les systèmes planétaires. |
 | 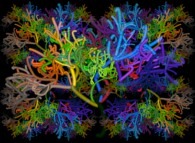 |  | 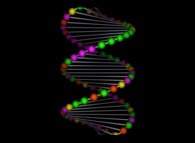 | La Nature et la Vie, la Terre est notre Berceau. |
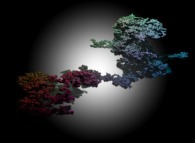 |  |  | La Complexité émergeant du Chaos. |
 | 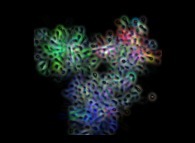 | Molécules, Atomes et Particules Elémentaires. |
-19
2.0 10 mètre
Terra Incognita (Mathematica ?)...
 | L'Espace-Temps, l'Echelle de Planck et au-delà... |
-35
1.6 10 mètre
La borne supérieure (8.8 10+26 mètres) correspond à l'univers observable et ne tient pas compte de sa possible
extension infinie non plus que de la notion de Multivers. Quant à la borne inférieure (1.6 10-35 mètre),
appelée échelle de Planck, elle est le point de rencontre entre la Relativité Générale et la Mécanique Quantique. Il
convient de noter qu'entre cette dernière et ce que l'on sait atteindre en laboratoire (2.0 10-19 mètre) il y a seize
ordres de grandeur. Ceux-ci ne peuvent être franchis à l'aide des techniques "traditionnelles" et peut-être que seules
les Mathématiques permettront d'explorer cette Terra Incognita, comme nous le verrons
au paragraphe 2.3 et suivants...
2.2-LA MODELISATION (LES MATHEMATIQUES, UN LANGAGE ET UNE MEMOIRE) :
Le mot Mathématique vient du grec Mathêma (science, connaissance).
Pour les anciens grecs, tout était nombre et pour Galilée, au XVI-XVIIe siècle, le grand livre de la Nature
était écrit en langage mathématique. Le physicien doit pouvoir consigner, mémoriser et transmettre, de façon objective et précise,
le résultat de ses observations et de ses mesures. Les langues naturelles, quelles qu'elles soient, ne le permettent pas, contrairement aux
Mathématiques...
Les succès remportés en Physique grâce à elles sont considérables (comme nous le verrons en particulier
au paragraphe 2.3) mais malgré tout, ils restent mystérieux
et Eugène Wigner, Prix Nobel de Physique en 1963,
s'interrogeait déjà sur le pourquoi de cette redoutable efficacité.
Ne seraient-elles qu'un "vulgaire" outil de compression de mesures, la régularité impliquant la compressibilité [08] ?
Ou bien sont-elles plus que cela ? Mais alors,
le mathématicien est-il un créateur (celui qui tire du néant...) ou bien un explorateur (celui qui parcourt en observant) ou encore les deux à la fois
[09] ?
Cette conception platonicienne d'une existence des Mathématiques indépendantes de l'Homme font qu'alors elles sont les mêmes aux "quatre coins de l'Univers"
[10]. Mais alors, où sont-elles gravées ?
Cette question pourrait sembler un défaut rédhibitoire d'une telle conception. Mais s'interroge-t-on sur la loi de la gravitation de
Newton : comment la matière sait-elle que l'interaction doit être inversement proportionnelle au carré de la distance ?
Ou bien encore, plus difficile : où est l'Univers, où est notre Multivers ?
Certains, comme Max Tegmark au MIT, adoptent une position extrème : les Mathématiques sont efficaces en Physique "tout simplement"
parce que les Mathématiques sont LA Réalité et l'Homme n'est qu'une entité mathématique consciente. La Physique ne serait alors qu'une approximation,
meilleure de jour en jour, des Mathématiques [11] !
Mais si tel est le cas, que pensez de l'arbitraire des axiomes, de l'incomplétude de Kurt Gödel
ou encore de toutes les questions auxquelles elles devraient pouvoir répondre
(Pourquoi quelque chose plutot que rien ? Qu'est-ce que la non existence ? Dieu existe-t-il ? Qu'est-ce que le beau ?...) ?
[Plus d'informations sur ce sujet]
2.3-LA PREDICTION (LES MATHEMATIQUES, UNE PENSEE, MAIS AUSSI UN "INSTRUMENT D'OPTIQUE" REVOLUTIONNAIRE) :
Au XIXe siècle, Heinrich Hertz avait écrit : On ne peut échapper au sentiment que ces formules mathématiques
ont une existence qui leur est propre, qu'elles sont plus savantes que
ceux qui les ont découvertes, et que nous pouvons en extraire plus de science
qu'il n'en a été mis à l'origine.
Grâce à trois exemples historiques de découvertes faites par le calcul, expliquons comment les équations peuvent être plus "intelligentes" que leurs auteurs :
- La découverte de la planète Neptune par Urbain Le Verrier en 1846 :
Les progrès scientifiques se font à la fois sur le plan expérimental [12]
et sur le plan mathématique. Or, au
milieu du XIXe siècle une petite disparité était apparue entre les positions mesurées des
planètes alors connues dans le système solaire et celles que permettaient de calculer les
lois de Newton qui régnaient alors en maître. Deux solutions étaient alors envisageables : soit considérer
que les lois (de Newton) n'étaient pas les bonnes, soit que le "contexte" dans lequel elles étaient
appliquées n'étaient pas le bon [13].
Urbain Le Verrier choisit cette dernière voie et introduisit alors une
"nouvelle" planète dans le système solaire que l'on baptisa Neptune après la confirmation observationnelle de son existence.
- La découverte de l'expansion de l'Univers au début du XXe siècle :
Après avoir publié en 1905 la Théorie de la Relativité Restreinte
(ainsi que trois autres articles fondamentaux relatifs
à l'effet photoélectrique, au mouvement brownien et à l'équivalence masse-énergie),
Albert Einstein publia en 1915 la Théorie
de la Relativité Générale. Celle-ci s'imposa rapidement comme un nouveau modèle de la gravitation
et il remplaça alors celui de Newton. Il permettait, pour la première fois, de
traiter et manipuler globalement l'Univers comme un objet scientifique. Albert Einstein avait, au moment de
cette découverte, l'intime conviction que l'Univers était statique. Or les physiciens
qui se mirent au travail sur ses équations [14] constatèrent
rapidement que l'Univers ne pouvait qu'être en évolution. Cela fut vérifié quelques années
plus tard par Edwin Hubble qui observa que plus les galaxies étaient éloignées de nous,
plus elles semblaient nous fuir rapidement. L'Univers était donc en expansion et en remontant le
temps, l'Univers avait dû connaître une phase très dense : c'est le modèle du Big Bang [15]
Ainsi, sans vouloir offenser la mémoire d'Albert Einstein, plus de phénomènes que lui-même
avait injectés dans ses équations en furent extraits.
On notera au passage que c'est aussi cette théorie qui a permis de comprendre l'anomalie de l'avance
du périhélie de Mercure, par une démarche contraire à celle d'Urbain Le Verrier
consistant cette fois-ci à changer les lois et non point le contexte...
- La découverte de l'anti-matière par Paul Dirac en 1930 :
Lors de son étude de l'électron, à la fois quantique et relativiste,
il écrivit une équation qui porte aujourd'hui son nom. Celle-ci possédait deux solutions
de signes opposés : l'une correspondait à l'électron. L'autre
devait, pour Paul Dirac, correspondre à une particule de même nature
mais de charge positive : ce fut la découverte de l'anti-électron
confirmée expérimentalement par la suite.
On remarquera dans les exemples précédents que bien souvent les prédictions faites sont contraires à l'intuition.
Cela est particulièrement vrai avec la Mécanique Quantique où l'existence des phénomènes dits de
non localité et d'intrication, issus des réflexions de Niels Bohr, Albert Einstein [16] ou encore
John Bell [17], a été confirmée dans les années 1980 par les remarquables expériences d'Alain Aspect (Prix Nobel de Physique en 2022).
Cela doit donc nous rappeler que tout modèle doit être réfutable :
les prédictions de nature mathématique doivent ensuite être vérifiées par des expériences réelles
(par opposition avec les expériences virtuelles présentées par la suite),
généralement fort délicates, voire impossibles, comme, par exemple, avec les deux conjectures suivantes :
2.4-LE MATHEMATICIEN ET LE PHYSICIEN :
Notons au préalable que l'honnête homme de Montaigne n'est plus. Il est loin le temps où il était
possible de connaître et maîtriser l'ensemble des Mathématiques, de la Physique, de la Philosophie,...
Aujourd'hui, la spécialisation est inévitable : on peut évidemment le regretter, mais les choses sont ainsi.
Cela implique donc nécessairement des relations et des coopérations inter-disciplinaires, en particulier entre mathématiciens
et physiciens. Donnons en un exemple :
Dans les années 1980, Bernard Sapoval et ses collègues étudiaient le phénomène de la diffusion.
Sa compréhension est essentielle car, en effet, il est présent dans la plupart des
mécanismes du vivant [18], joue un rôle important dans l'industrie [19]
et se retrouve aussi dans bien d'autres phénomènes [20].
 Cette image montre le résultat d'un calcul au cours duquel des particules (vertes),
sont émises par une source située dans la partie inférieure d'un espace bidimensionnel (bleu) initialement vide. Ces particules, au cours du temps,
se déplacent aléatoirement en pouvant sauter vers l'une de leurs cases voisines les plus proches, à condition
que celle-ci soit inoccupée. Au bout d'un certain temps le front dit de diffusion
(jaune) possède une forme très irrégulière : sa géométrie est fractale (notion qui sera
définie paragraphe 2.7) et il est caractérisé
par un nombre [21] qui est une mesure
de son irrégularité et de sa façon d'occuper, de remplir le plan. Bernard Sapoval avait alors conjecturé que ce nombre
devait être égal à 7/4. La démonstration de cette étonnante propriété a dû attendre de nombreuses
années et cette performance fut accomplie par Greg Lawler, Pierre Nolin, Oded Schramm, Stanislas Smirnov et Wendelin Werner (Médaille Fields 2006).
Cette image montre le résultat d'un calcul au cours duquel des particules (vertes),
sont émises par une source située dans la partie inférieure d'un espace bidimensionnel (bleu) initialement vide. Ces particules, au cours du temps,
se déplacent aléatoirement en pouvant sauter vers l'une de leurs cases voisines les plus proches, à condition
que celle-ci soit inoccupée. Au bout d'un certain temps le front dit de diffusion
(jaune) possède une forme très irrégulière : sa géométrie est fractale (notion qui sera
définie paragraphe 2.7) et il est caractérisé
par un nombre [21] qui est une mesure
de son irrégularité et de sa façon d'occuper, de remplir le plan. Bernard Sapoval avait alors conjecturé que ce nombre
devait être égal à 7/4. La démonstration de cette étonnante propriété a dû attendre de nombreuses
années et cette performance fut accomplie par Greg Lawler, Pierre Nolin, Oded Schramm, Stanislas Smirnov et Wendelin Werner (Médaille Fields 2006).
Ainsi donc, le physicien pose des problèmes et émet des conjectures auquel le mathématicien s'attaque formellement...
Monsieur Jourdain, dans le Bourgeois Gentilhomme de Molière, disait de la prose sans qu'il en sût rien.
Or l'histoire des Mathématiques et de la Physique montre que le mathématicien fait parfois de la Physique sans en avoir pleinement conscience.
En voici quelques exemples :
- Evariste Galois et les groupes : à la base de toute la Physique contemporaine,
- Bernhard Riemann et les variétés éponymes : à la base de la Relativité Générale (et donc essentielles pour le 'GPS' -Navstar Global Positionning System- !),
- Les mathématiciens des monstres continus non différentiables (Weierstrass,
Cantor, Peano, Lebesgue, Hausdorff, Besicovitch, von Koch, Sierpinski,...) : à la base de la Géométrie Fractale
qui sera présentée au paragraphe 2.7.
Alors, peut-on généraliser et dire que le mathématicien fait toujours de la Physique sans le savoir ?
Cela serait vrai si effectivement la Réalité ultime était, comme cela fut évoqué précédemment,
faite des Mathématiques... Mais quelle que soit la "situation", l'éternité des vérités des Mathématiques
est à opposer à la précarité de celles de la Physique...
2.5-MATHEMATIQUES, CALCUL ET INFORMATIQUE :
Il est impossible de décrire les liens tissés entre les Mathématiques et la Physique
au cours des siècles sans évoquer le calcul et la programmation. Rappelons au préalable les noms de quelques
grands précurseurs, dont beaucoup furent des mathématiciens :
- John Neper (les logarithmes et la règle à calculs, XVIe-XVIIe siècles),
- Blaise Pascal (la machine à additionner, XVIIe siècle),
- Gottfried Wilhelm Leibniz (la machine à multiplier, XVIIe siècle),
- Jacques de Vaucanson (les automates, XVIIe siècle),
- Joseph Marie Jacquard (le métier à tisser programmable, XVIIIe siècle),
- Charles Babbage et Lady Ada Lovelace (la première machine possédant une mémoire et une unité de calcul ou moulin [22], XIXe siècle),
- etc...
Issues principalement des vingt-trois problèmes de Hilbert [23],
les notions d'algorithme et de calculabilité ont émergé au cours des années 1930 sous l'impulsion
d'Alonzo Church, de Kurt Gödel, d'Alan Turing et de John von Neumann. C'est alors que furent définis les grands principes des
ordinateurs d'aujourd'hui, machines à calculer programmables. Ces fondements n'ont pas radicalement changé par la suite, même
si des progrès matériels et logiciels considérables ont été accomplis. Les performances et l'ergonomie des machines actuelles permettent
des activités autrement impossibles et en particulier de faire, si besoin est, des Mathématiques une science expérimentale.
En voici quelques exemples :
 La recherche d'un contre-exemple de la conjecture de Goldbach.
L'axe vertical de cette image porte le "rang" des nombres premiers strictement supérieurs à 2 (0 pour 3, 1 pour 5, 2 pour 7, ...).
Quant à l'axe horizontal, il montre tous les nombres pairs à partir de 6 (et non pas 4) et à la verticale de chacun d'eux,
toutes leurs décompositions possibles, la même couleur étant utilisée
pour les deux nombres premiers d'un même couple.
La recherche d'un contre-exemple de la conjecture de Goldbach.
L'axe vertical de cette image porte le "rang" des nombres premiers strictement supérieurs à 2 (0 pour 3, 1 pour 5, 2 pour 7, ...).
Quant à l'axe horizontal, il montre tous les nombres pairs à partir de 6 (et non pas 4) et à la verticale de chacun d'eux,
toutes leurs décompositions possibles, la même couleur étant utilisée
pour les deux nombres premiers d'un même couple.
 La disposition "équitable" de N points sur une sphère. Alors que la chose est triviale sur
un cercle, elle est impossible à faire rigoureusement sur la sphère. Seule est possible une méthode reposant sur des essais aléatoires destinés
à améliorer un certain critère.
La disposition "équitable" de N points sur une sphère. Alors que la chose est triviale sur
un cercle, elle est impossible à faire rigoureusement sur la sphère. Seule est possible une méthode reposant sur des essais aléatoires destinés
à améliorer un certain critère.
 Le jeu de la vie de John Conway. Simultanément aux développements des ordinateurs, eurent
lieu des recherches concernant des systèmes abstraits et élémentaires appelés automates. Il s'agit de systèmes de particules résidant en
général sur les nœuds de réseaux carrés et évoluant au cours du temps en suivant des lois de vie et de mort extrémement simples.
En fonction des conditions initiales et des lois exactes utilisées, des systèmes aux comportements étonnants, éventuellement
auto-reproducteurs, peuvent être conçus. Ils montrent clairement que du simple peut émerger le complexe.
Le jeu de la vie de John Conway. Simultanément aux développements des ordinateurs, eurent
lieu des recherches concernant des systèmes abstraits et élémentaires appelés automates. Il s'agit de systèmes de particules résidant en
général sur les nœuds de réseaux carrés et évoluant au cours du temps en suivant des lois de vie et de mort extrémement simples.
En fonction des conditions initiales et des lois exactes utilisées, des systèmes aux comportements étonnants, éventuellement
auto-reproducteurs, peuvent être conçus. Ils montrent clairement que du simple peut émerger le complexe.
Mais l'usage de l'ordinateur ne s'arrète pas là. Il est évident qu'il joue un rôle important dans le domaine
du traitement de textes mathématiques, mais aussi et surtout en apportant une aide appréciable pour la
démonstration de théorèmes en fournissant une assistance ou encore pour une aide à la vérification formelle.
Malgré ces points évidemment très positifs, il est impossible de ne pas s'interroger sur le rôle de plus en plus (trop ?) important
joué par l'ordinateur, en particulier à l'intérieur de toutes les disciplines scientifiques,
en n'oubliant pas que Pythagore, Galilée, Newton, Einstein,... ne connaissaient pas l'informatique !
2.6-L'EXPERIMENTATION VIRTUELLE (LES MATHEMATIQUES, UN "LABORATOIRE" UNIVERSEL) :
Il y a plusieurs siècles, notre vision du monde fut bouleversée par l'invention du microscope et celle du télescope.
Le premier nous révéla des objets trop petits pour être vus à l'œil nu,
alors que le second nous dévoilait la "profondeur" des cieux.
Les Mathématiques en tant que langage de la Physique, associées à l'informatique, nous permettent
aujourd'hui de mettre en œuvre une approche expérimentalle nouvelle : celle de l'Expérimentation Virtuelle
par opposition à l'Expérimentation Réelle.
Une expérience réelle consiste à
manipuler, observer et mesurer de "vrais objets" [24].
Une expérience Virtuelle utilisera, quant à elle, non pas de "vrais objets"
mais leur modèle mathématique. Ce dernier sera traduit en algorithmes, puis en programmes
destinés, par exemple, à calculer au cours du temps les valeurs de certaines
grandeurs pertinentes [25]. Ensuite ces résultats numériques seront
mis en images afin de permettre à l'expérimentateur virtuel d'une part, de mieux appréhender la "montagne"
de valeurs calculées et d'autre part, d'interagir avec les équations
et les différents paramètres. Une limite (nous en verrons d'autres
au paragraphe 2.8) à ce processus est celle de la nécessaire existence
de la description mathématique du phénomène étudié, mais dès que celle-ci est
validée, "tout" est permis et en particulier des expériences autrement impossibles.
Donnons un exemple de cela :
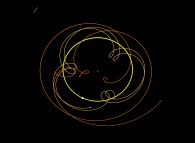 Le système solaire géocentrique.
Même si Aristarque de Samos (~310-230 avant Jésus Christ),
ou encore Hypatie d'Alexandrie (quatrième siècle de notre ère),
avaient tenté
d'imposer sans succès une autre vision, pendant de nombreux siècles notre Terre fut
considérée comme étant le centre du Monde : le Soleil tournait autour et les planètes alors
connues décrivaient dans le ciel de régulières boucles dites de rétrogradation.
C'était le modèle des épicycles de Ptolémée (astronome grec du deuxième siècle de notre ère).
Mais les progrès accomplis en matière d'observation [26]
et de mesure [27]
rendirent cette description de plus en plus difficilement acceptable.
Le système solaire géocentrique.
Même si Aristarque de Samos (~310-230 avant Jésus Christ),
ou encore Hypatie d'Alexandrie (quatrième siècle de notre ère),
avaient tenté
d'imposer sans succès une autre vision, pendant de nombreux siècles notre Terre fut
considérée comme étant le centre du Monde : le Soleil tournait autour et les planètes alors
connues décrivaient dans le ciel de régulières boucles dites de rétrogradation.
C'était le modèle des épicycles de Ptolémée (astronome grec du deuxième siècle de notre ère).
Mais les progrès accomplis en matière d'observation [26]
et de mesure [27]
rendirent cette description de plus en plus difficilement acceptable.
Au passage, il convient de noter que malgré tout ce modèle était défendable,
puisqu'en effet les apparences
militaient en sa faveur[28].
De plus, cet exemple illustre concrètement la précarité des vérités de la Physique
qui fut évoquée au paragraphe 2.4.
 Le système solaire héliocentrique.
En 1543, une révolution éclata : le moine polonais
Nicolas Copernic [29] mit le Soleil au
centre du système solaire, faisant par la-même de notre Terre une planète
comme les autres. Puis en 1609, Johannes Kepler (Astronomia Nova) décrivit
la trajectoire des planètes [30] par des ellipses
dont l'un des deux foyers était le Soleil.
Enfin, en 1687, Sir Isaac Newton publia ses fameux
Philisophiae Naturalis Principia Mathematica
dans lesquels les lois de la mécanique classique
firent leur apparition [31].
Le système solaire héliocentrique.
En 1543, une révolution éclata : le moine polonais
Nicolas Copernic [29] mit le Soleil au
centre du système solaire, faisant par la-même de notre Terre une planète
comme les autres. Puis en 1609, Johannes Kepler (Astronomia Nova) décrivit
la trajectoire des planètes [30] par des ellipses
dont l'un des deux foyers était le Soleil.
Enfin, en 1687, Sir Isaac Newton publia ses fameux
Philisophiae Naturalis Principia Mathematica
dans lesquels les lois de la mécanique classique
firent leur apparition [31].
 Rajoutons une nouvelle planète dans le système solaire.
Introduisons donc correctement [32]
une nouvelle planète suivant seize trajectoires différentes,
toutes en dehors du plan de l'écliptique.
Rajoutons une nouvelle planète dans le système solaire.
Introduisons donc correctement [32]
une nouvelle planète suivant seize trajectoires différentes,
toutes en dehors du plan de l'écliptique.
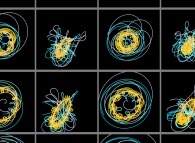 Un système solaire à l'apparence chaotique.
Les astronomes de cette planète observent des trajectoires (apparentes !) très
différentes des épicycles de Ptolémée en particulier par l'absence de périodicités évidentes.
Leur travail aurait certainement été beaucoup plus difficile que celui de Nicolas Copernic !
Un système solaire à l'apparence chaotique.
Les astronomes de cette planète observent des trajectoires (apparentes !) très
différentes des épicycles de Ptolémée en particulier par l'absence de périodicités évidentes.
Leur travail aurait certainement été beaucoup plus difficile que celui de Nicolas Copernic !
Ainsi, en plus de leur rôle fondamental, les Mathématiques sont bel et bien un nouvel instrument d'optique.
Mais attention au piège du je calcule, donc je suis...
2.7-UNE BRANCHE RECENTE DES MATHEMATIQUES, LA GEOMETRIE FRACTALE :
Il est intéressant de présenter une avancée récente, rencontre des
Mathématiques pures et des Mathématiques appliquées : la Géométrie Fractale.
Jusqu'à un passé récent, des questions naïves restaient sans réponse
et par exemple : quel est la forme d'une montagne, d'un nuage ou encore d'un arbre ? Pour y répondre il fallu
s'éloigner (provisoirement...) de la Nature comme nous allons le voir.
Pour dire les choses de façon non formelle, on dit qu'une courbe est continue
s'il est possible de la tracer sur une feuille de papier sans lever le crayon. Une fois
qu'elle est dessinée, on constate qu'en chacun de ses points il est possible
de tracer une tangente [33]. Jusqu'au milieu
du XIXe siècle, on associait les propriétés de continuité et de dérivabilité [34].
Or des mathéticiens tels Weierstrass, Cantor, Peano, von Koch,
Sierpinski,... imaginèrent des courbes continues mais sans tangente [35].
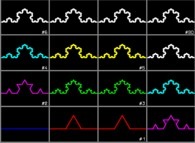 Donnons un exemple d'une telle "monstruosité" : la courbe de von Koch.
D'après ce qui vient d'être dit, il est évident que ces courbes ne peuvent être
tracées exactement car, en effet, sinon cela signifierait l'existence des tangentes.
Seules des approximations peuvent être présentées. Mais cela ne doit pas nous choquer : c'est
aussi le cas dans bien d'autre circonstances et par exemple lorsque l'on montre les premières décimales de pi...
La courbe de von Koch, comme tous les autres "objets" fractals, est définie par
une règle de construction indéfiniment répétée [36]
et c'est seulement à la limite qu'apparaitrait le "monstre" [37].
Cette règle apparait dans les trois cases en bas et à gauche de la figure : elle consiste à
remplacer le tiers central d'un grand segment (00 en bleu) par les deux côtés supérieurs d'un triangle
équilatéral (01 en rouge). Puis cette règle est répétée sur les quatres petits segments (01 en rouges) et encore répétée
indéfiniment sur des segments de plus en plus petits, mais de plus en plus nombreux...
Donnons un exemple d'une telle "monstruosité" : la courbe de von Koch.
D'après ce qui vient d'être dit, il est évident que ces courbes ne peuvent être
tracées exactement car, en effet, sinon cela signifierait l'existence des tangentes.
Seules des approximations peuvent être présentées. Mais cela ne doit pas nous choquer : c'est
aussi le cas dans bien d'autre circonstances et par exemple lorsque l'on montre les premières décimales de pi...
La courbe de von Koch, comme tous les autres "objets" fractals, est définie par
une règle de construction indéfiniment répétée [36]
et c'est seulement à la limite qu'apparaitrait le "monstre" [37].
Cette règle apparait dans les trois cases en bas et à gauche de la figure : elle consiste à
remplacer le tiers central d'un grand segment (00 en bleu) par les deux côtés supérieurs d'un triangle
équilatéral (01 en rouge). Puis cette règle est répétée sur les quatres petits segments (01 en rouges) et encore répétée
indéfiniment sur des segments de plus en plus petits, mais de plus en plus nombreux...
Deux propriétés communes à tous les objets fractals apparaissent : d'une part l'autosimilarité
qui signifie que le tout est identique aux parties ; ainsi, par exemple, sur la courbe de von Koch le motif rouge (01)
apparait quatre fois en plus petits sur la figure magenta (02). D'autre part, une quantité importante augmente tout au long
des itérations : il s'agit ici de la longueur ; et cela va très vite : si la longueur du segment bleu initial (00) était égale à un mètre,
alors la longueur totale de l'approximation située en haut et à droite (correspondant à l'itération numéro 90) serait
de 175.584.548.321 mètres [38], soit plus que la
distance de la Terre au Soleil ! A la limite, elle serait évidemment infinie alors qu'elle réside dans un domaine fini (et
petit) du plan.
Mais quel est le rapport entre ces deux propriétés et les montagnes, les nuages ou encore les arbres ?
En ce qui concerne l'autosimilarité, beaucoup d'objets naturels la possèdent, non point parfaitement
comme un objet purement mathématique, mais approximativement et imparfaitement. C'est par exemple le cas d'un chêne
(ou encore d'une fougère) :
sa plus grosse branche ressemble à une copie réduite de l'arbre entier et cela est aussi vrai des branches de plus en plus petites.
Pour ce qui est de côtoiement du fini et de l'infini, l'exemple des alvéoles pulmonaires de nos poumons l'illustre parfaitement : logées dans un
volume restreint, leur surface totale est comprise entre 100 et 200 mètres carrés [39] !
La Géométrie Fractale permet donc au fini et à l'infini de cohabiter et donc de satisfaire des contraintes
qu'aucune autre géométrie ne pourrait supporter [40].
Révéler le lien entre ces monstres du XIXe siècle et la Nature fut la contribution géniale de Benoît Mandelbrot.
A partir des années 1960 et ensuite très rapidement cette nouvelle géométrie a envahi la Physique, la Finance
mais aussi l'Art comme nous allons le voir.
Des structures fractales universelles émergent de processus abstraits ou physiques divers et simples :
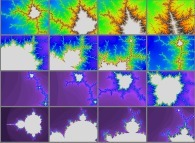 L'ensemble de Mandelbrot : l'itération d'une transformation élémentaire du second
degré [41] dans le plan complexe conduit à un extraordinaire objet
pour lequel l'autosimilarité est évidente sur les quelques images de ce zoom.
L'ensemble de Mandelbrot : l'itération d'une transformation élémentaire du second
degré [41] dans le plan complexe conduit à un extraordinaire objet
pour lequel l'autosimilarité est évidente sur les quelques images de ce zoom.
 Un agrégat fractal : des petites particules initialement bien rangées
(en bas et àgauche) sont animées d'un mouvement aléatoire. Leur seule propriété utile est d'être
collante. Ainsi au cours du temps, des agrégats de plus en plus gros se forment jusqu'à aboutir à
un unique agrégat fractal (en haut et à droite).
Un agrégat fractal : des petites particules initialement bien rangées
(en bas et àgauche) sont animées d'un mouvement aléatoire. Leur seule propriété utile est d'être
collante. Ainsi au cours du temps, des agrégats de plus en plus gros se forment jusqu'à aboutir à
un unique agrégat fractal (en haut et à droite).
 Les côtes maritimes : suivant le modèle d'Andrea Baldassarri, Andrea Gabrielli et
Bernard Sapoval, la "force" d'attaque de la mer est inversement proportionnelle à la longueur des côtes. Ces dernières n'offrent
pas partout la même résistance. Là où
elles sont friables, il y a érosion, la mer pénètre alors dans les terres, la longueur des côtes augmente et ainsi
la force décroit : un équilibre relatif correspondant à une structure fractale s'établit.
Les côtes maritimes : suivant le modèle d'Andrea Baldassarri, Andrea Gabrielli et
Bernard Sapoval, la "force" d'attaque de la mer est inversement proportionnelle à la longueur des côtes. Ces dernières n'offrent
pas partout la même résistance. Là où
elles sont friables, il y a érosion, la mer pénètre alors dans les terres, la longueur des côtes augmente et ainsi
la force décroit : un équilibre relatif correspondant à une structure fractale s'établit.
Traditionnellment, on fait une distinction entre la Géométrie Fractale déterministe (où le hasard n'intervient
pas, même si parfois d'étonnantes formes apparaissent) et la Géométrie Fractale non déterministe (où le hasard
intervient) et qui est celle qui est utile à la description mathématique de nombreux phénomènes naturels. Présentons
quelques images illustrant cela :
Si l'on étend la définition d'un objet fractal avec la propriété de posséder des structures à
toutes les échelles d'observation, alors la Réalité (et la Science donc...)
serait l'ultime objet fractal !
2.8-LES LIMITES FONDAMENTALES (DE LA CONNAISSANCE, DE NOS "OUTILS",...) :
Il convient de rappeler une évidence : Nous ne percevons pas, nous ne voyons pas toute la Réalité.
A titre d'exemple, la théorie dite des super-cordes attribue onze dimensions à notre Univers,
au lieu des quatre qui nous sont familières ! Qu'elles soient "infiniment" petites ou "infiniment" grandes, il est clair que nos sens ne nous les révèlent pas.
Alors combien encore d'autres mystères nous sont cachés ?
Et même si la Réalité est mathématique, elle ne nous est pas révélée globalement par quelque tour de baguette magique : c'est à nous de l'approcher
pas à pas, à tâtons...
Quelle que soit la nature des Mathématiques, Kurt Gödel a démontré dans les années 1930 leur incomplétude sous
la forme de deux théorèmes : le premier nous dit que tout système axiomatique assez puissant pour inclure l'arithmétique
contient des propositions dites indécidables c'est-à-dire dont on ne peut dire ni si elles sont
vraies, ni si elles sont fausses. A titre d'exemple l'Hypothèse du Continu (HC) dont il a déjà été question
au paragraphe 1
est un indécidable de la théorie des ensembles "standard" (ZFC). Le second théorème de Gödel affirme que la propriété
pour un système axiomatique d'être cohérent [42] est un indécidable de ce système.
Si la Physique est en réalité une approximation toujours meilleure des
Mathématiques, quelles sont les conséquences de ces deux théorèmes en ce qui concerne notre connaissance de l'Univers ?
L'indécidabilité pourrait-elle engendrer la multiplicité ?
Précedemment, nous avons montré par l'exemple que les images facilitaient la médiation entre les modèles et leurs auteurs,
tout en étant de plus des champs de découverte. Mais sont-elles faciles à réaliser ? Sont-elles neutres ? Les réponses à ces questions sont
malheureusement négatives. Et les raisons pour cela ne manquent pas :
Nous avons noté le rôle (trop ?) important de l'ordinateur. Utiliser un ordinateur, c'est le programmer,
c'est-à-dire lui donner la suite des instructions qu'il devra exécuter pour accomplir une certaine tâche. Les
programmes utiles contiennent bien souvent des milliers, voire des millions de lignes ! Il n'est donc pas étonnant
que des anomalies plus ou moins subtiles y soient tapies. La programmation des ordinateurs n'est malheureusement pas une
Science, ni un Art. Elle relève plutot du domaine du bricolage où la rigueur des démonstrations des théorèmes
n'est pas de mise ! La vigilance s'impose donc à la lecture des résultats ou lors de l'observation des images calculées.
On notera au passage que même si la fiabilité des machines d'aujourd'hui n'a plus rien à voir avec celle des machines d'hier,
il n'empèche qu'elles peuvent tomber en panne et causer alors la perte irrémédiable d'une partie
de notre patrimoine culturel et scientifique.
Mais lors de l'usage d'un ordinateur les difficultés liées à la programmation ne sont pas les seules. En
effet, comme nous l'avons déjà rappelé, un ordinateur est avant toute chose une machine à
calculer. La question de savoir si elle une machine à bien calculer doit donc être posée...
La réponse négative apportée par le programme suivant [43]
en surprendra plus d'un :
main()
{
double B=4095.1;
double A=B+1;
double x=1;
int n;
printf("initialisation x = %.16f\n",x);
for (n=1 ; n <= 9 ; n++)
{
x = (A*x) - B;
printf("iteration %01d x = %+.16f\n",n,x);
}
}
En fait, ce programme transforme le nombre 'x' initialisé avec la valeur 1, de façon à ce qu'il
conserve cette valeur. En effet :
x --> (A*x) - B --> (A*1)-B --> A-B --> 1
or voici les résultats obtenus :
initialisation x = +1.0000000000000000
iteration 1 x = +1.0000000000004547
iteration 2 x = +1.0000000018630999
iteration 3 x = +1.0000076314440776
iteration 4 x = +1.0312591580864137
iteration 5 x = +129.0406374377594148
iteration 6 x = +524468.2550088063580915
iteration 7 x = +2148270324.2415719032287598
iteration 8 x = +8799530071030.8046875000000000
iteration 9 x = +36043755123945184.0000000000000000
Avant d'expliquer le phénomène, il convient de noter au préalable que ce programme possède deux propriétés exceptionnelles dans l'univers
des programmes : d'une part, il est trivial et ne peut contenir d'erreur. D'autre part, la réponse
(x=1) est connue à l'avance !
La cause de cette violente anomalie a déjà été évoquée lorsqu'il fut question de la conjecture des
nombres premiers jumeaux au paragraphe 1 :
un ordinateur est "tout simplement" une machine aux capacités finies. Dans l'exemple
précédent, les constantes décimales simples B=4095.1 et A=4096.1 demandent en fait une infinité de chiffres
binaires (ou bits) pour être représentées exactement et dans ce programme la
différence A-B n'était pas exactement égale à 1. Mais évidemment le problème ne se limite pas à
un simple changement de base : il est beaucoup plus général et concerne donc l'impossibilité de représenter et
manipuler l'infini dans nos machines. Or c'est là une limite très importante puisque les nombres réels sont inévitables en Physique.
Les conséquences de cela sont nombreuses et malheureusement largement sous-estimées !
On notera enfin que la Géométrie Fractale (comme cela fut dit
au paragraphe 2.7) nous avait fait passer de
la continuité différentiable à la continuité non différentiable. On peut se demander aujourd'hui
si l'ordinateur ne va pas nous contraindre à passer à la non continuité non différentiable et peut-être
ainsi nous révéler de nouvelles vérités concernant notre Univers (serait-il lui-même discontinu ?)...
3-ARTS ET MATHEMATIQUES, MATHEMATIQUES ET ARTS :
Créer ou chercher : il y a certainement assez peu de différences entre ces deux activités intellectuelles et il n'est sonc pas surprenant
que les Mathématiques et les Arts entretiennent d'étroites relations.
Depuis des siècles les Mathématiques sont au service des Arts :
Mais les Arts peuvent aussi être au service des Mathématiques :
Cette rencontre peut aujourd'hui se prolonger avec la notion d'œuvre potentielle. Dans ce contexte, l'œuvre n'est
plus l'image mais bien plutot le modèle mathématique sous-jacent qui contient en lui une infinité d'œuvres du même type [44],
tout comme le compas contient une infinité de cercles. En voici quelques exemples :















4-CONCLUSION :
Les Mathématiques sont notre meilleur (et unique ?) "outil" pour approcher (asymptotiquement ou "fractalement" ?) la Réalité et
il n'est pas impossible qu'elles soient cette Réalité. Alors, la Recherche en Mathématiques (et en Physique,...)
est peut-être l'ultime aventure moderne... Au niveau de l'enseignement, au-dela de leur rôle sélectif, il conviendra
de ne pas oublier leur rôle structurant fondamental.
Mais, certainement de façon utopique (voire naïve), peut-être vont-elles sauver l'Humanité. En effet, notre Terre va
mal : besoin d'innovation [45], pollution, épuisement irréversible de nombreuses ressources naturelles, changement climatique,... Le besoin de
comprendre ce qu'il se passe, de maîtriser, de prévoir les évolutions à long terme,... impliquent
une description objective des phénomènes.
Donnons deux exemples concrets : le premiet est relatif à l'énergie dont sa production par les filières
nucléaires (quel que soit le bien ou le mal que l'on puisse en penser) est issue de recherches menées sur la structure de la
matière au début du XXe siècle par des pionners [46]
de façon très abstraite, grâce à la Mécanique Quantique.
Le second est celui du 'GPS' qui ne fonctionnerait pas avec
la précision qui le caractérise aujourd'hui si Bernhard Riemann ne s'était pas intéressé aux variétés éponymes et
si Albert Einstein ne les avait pas utilisées comme base de sa Relativité Générale.
Et toutes ces recherches sans applications a priori
révélèrent les énergies titanesques tapies au cœur de la matière que l'Homme a su ensuite exploiter industriellement (et militairement malheureusement).
Alors peut-être que les recherches sur les nombres premiers ou encore celles sur les dimensions supplémentaires de l'espace-temps,
sans utilités pratiques a priori nous fourniront, elles aussi, les clefs d'un monde meilleur...
Sans Recherche appliquée et fondamentale pas de Découvertes !
[01]
- Il a été
démontré par Kurt Gödel en 1938 que la négation de HC n'était pas démontrable dans le
cadre du système axiomatique "standard" de la théorie des ensembles (ZFC -Zermelo, Frankel, axiome du Choix-), puis par Paul Cohen
en 1963 qu'il en était de même pour HC. Ainsi HC est une proposition dite indécidable de ZFC et donc de
nouveaux axiomes doivent être introduits pour pouvoir progresser. Les travaux actuels, en particulier ceux de Hugh Woodin, laissent entrevoir une solution définitive
à ce problème fondamental (la théorie des ensembles constituant la base des Mathématiques).
[02]
- Très simple à démontrer...
[03]
- Et d'ailleurs est-il possible de dessiner ne serait-ce qu'un seul "vrai" triangle rectangle dont
l'angle droit mesurerait exactement 90 degrés et dont les côtés n'auraient pas d'épaisseur ?
[04]
- Ni dans ses notes publiées cinq ans après sa mort par son fils,
ni dans la copieuse correspondance qu'il entrenait avec les plus grands savants de son temps
(Bernoulli, Desargues, Descartes, Mersenne, Pascal, Wallis,...).
[05]
- Sir Andrew Wiles après cet exploit.
[06]
- Contrairement au théorème de Pythagore qui lui, sert en permanence à mesurer des distances.
[07]
- A comparer aux 7.500 tonnes de la Tour Eiffel...
[08]
- Un peu comme la compression JPEG des images n'est possible que parce que leur contenu n'est pas aléatoire.
[09]
- Comme je le crois : "Dieu a fait les nombres entiers, tout le reste est l'œuvre de l'homme" (Leopold Kronecker, 1891).
[10]
- On notera que c'est l'hypothèse de base du physicien en ce qui concerne les lois de la nature.
[11]
- Ce n'est alors plus le physicien qui fait des Mathématiques, mais le mathématicien qui fait de la Physique...
[12]
- En particulier au niveau de la mesure du temps, de l'espace,...
[13]
- Ce que Galilée fit en son temps pour la chute des corps.
[14]
- En particulier l'abbé Georges Lemaître.
[15]
- Celui-ci a beaucoup évolué au cours des dernières années en y intégrant la Mécanique
Quantique, le principe de l'inflation ou encore la notion de Multivers.
[16]
- Paradoxe EPR -Einstein, Podolsky, Rosen-.
[17]
- Et le théorème éponyme.
[18]
- Respiration au niveau des alvéoles pulmonaires, fonctionnement interne des cellules,...
[19]
- Soudure, fabrication des circuits intégrés,...
[20]
- Par exemple, la propagation des incendies de forêts.
[21]
- Il s'agit de la dimension dite fractale qui n'a aucune raison d'être un nombre entier.
[22]
- Malheureusement, l'électronique n'existant pas encore, ce premier ordinateur mécanique était voué à l'échec.
[23]
- En particulier de celui de la résolubilité des équations diophantiennes.
[24]
- Il a déjà été noté
au paragraphe 2.1
combien cela pouvait être difficile -et coûteux...- ; on ajoutera ici que ces "vrais objets",
par exemple les particules élémentaires, peuvent être en fait très éloignés des mains et des
yeux de l'expérimentateur.
[25]
- Par exemple des positions.
[26]
- Invention de la lunette astronomique.
[27]
- Du temps, des positions,...
[28]
- La trajectoire du Soleil dans notre ciel, l'immobilité apparente de la Terre telle que nous la ressentons,...
[29]
- De revolutionibus orbium caelestium libri VI.
[30]
- Y compris celle de la Terre évidemment.
[31]
- La description mathématique du système solaire qu'elles permirent alors
est d'ailleurs celle qui fut utilisée pour calculer ces quelques images.
[32]
- C'est-à-dire en respectant la troisième loi de Kepler (le carré de la période de révolution
est proportionnel au cube de la mesure du grand axe).
[33]
- C'est-à-dire une droite qui est la position limite d'une
sécante lorsque deux points d'intersection tendent l'un vers l'autre...
[34]
- Propriété qui se rapporte ici à l'existence de la tangente.
[35]
- Que Charles Hermite considérait d'ailleurs comme une plaie lamentable qu'il regardait avec effroi.
[36]
- On dit aussi itérée.
[37]
- Que l'on ne verra donc jamais exactement...
[38]
- C'est-à-dire 4/3 élevé à la puissance 90.
[39]
- Suivant les individus et l'âge.
[40]
- A titre d'information, si une surface d'échange de 200 mètres carrés
était réalisée à l'aide d'une sphère, celle-ci devrait avoir un diamètre de 8 mètres !
[41]
- Que nous ne détaillerons pas davantage.
[42]
- C'est-à-dire de ne pas permettre de démontrer à la fois une proposition et son contraire.
[43]
- Ecrit en langage C, on n'en explicitera ni la syntaxe, ni la sémantique, mais
pour en simplifier la lecture, sont mises en gras les parties essentielles.
[44]
- Concept qui n'aurait certainement pas déplu à Jorge Luis Borges, auteur de La bibliothèque de Babel.
[45]
- Le 'GPS' (Navstar Global Positionning System), fruit de
l'union de la Mécanique Quantique, de la Relativité Restreinte et de la Relativité Générale,
est certainement le meilleur exemple de l'apport des recherches les plus fondamentales aux technologies du quotidien...
[46]
- Tels Niels Bohr, Louis de Broglie, Paul Dirac, Albert Einstein, Werner Heisenberg,
Wolfgang Pauli, Max Planck, Erwin Schrödinger,...
Copyright © Jean-François COLONNA, 2013-2026.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2013-2026.






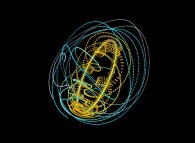










 Cette image montre le résultat d'un calcul au cours duquel des particules (vertes),
sont émises par une source située dans la partie inférieure d'un espace bidimensionnel (bleu) initialement vide. Ces particules, au cours du temps,
se déplacent aléatoirement en pouvant sauter vers l'une de leurs cases voisines les plus proches, à condition
que celle-ci soit inoccupée. Au bout d'un certain temps le front dit de diffusion
(jaune) possède une forme très irrégulière : sa géométrie est fractale (notion qui sera
définie paragraphe 2.7) et il est caractérisé
par un nombre [21] qui est une mesure
de son irrégularité et de sa façon d'occuper, de remplir le plan. Bernard Sapoval avait alors conjecturé que ce nombre
devait être égal à 7/4. La démonstration de cette étonnante propriété a dû attendre de nombreuses
années et cette performance fut accomplie par Greg Lawler, Pierre Nolin, Oded Schramm, Stanislas Smirnov et Wendelin Werner (Médaille Fields 2006).
Cette image montre le résultat d'un calcul au cours duquel des particules (vertes),
sont émises par une source située dans la partie inférieure d'un espace bidimensionnel (bleu) initialement vide. Ces particules, au cours du temps,
se déplacent aléatoirement en pouvant sauter vers l'une de leurs cases voisines les plus proches, à condition
que celle-ci soit inoccupée. Au bout d'un certain temps le front dit de diffusion
(jaune) possède une forme très irrégulière : sa géométrie est fractale (notion qui sera
définie paragraphe 2.7) et il est caractérisé
par un nombre [21] qui est une mesure
de son irrégularité et de sa façon d'occuper, de remplir le plan. Bernard Sapoval avait alors conjecturé que ce nombre
devait être égal à 7/4. La démonstration de cette étonnante propriété a dû attendre de nombreuses
années et cette performance fut accomplie par Greg Lawler, Pierre Nolin, Oded Schramm, Stanislas Smirnov et Wendelin Werner (Médaille Fields 2006).
 La recherche d'un contre-exemple de la conjecture de Goldbach.
L'axe vertical de cette image porte le "rang" des nombres premiers strictement supérieurs à 2 (0 pour 3, 1 pour 5, 2 pour 7, ...).
Quant à l'axe horizontal, il montre tous les nombres pairs à partir de 6 (et non pas 4) et à la verticale de chacun d'eux,
toutes leurs décompositions possibles, la même couleur étant utilisée
pour les deux nombres premiers d'un même couple.
La recherche d'un contre-exemple de la conjecture de Goldbach.
L'axe vertical de cette image porte le "rang" des nombres premiers strictement supérieurs à 2 (0 pour 3, 1 pour 5, 2 pour 7, ...).
Quant à l'axe horizontal, il montre tous les nombres pairs à partir de 6 (et non pas 4) et à la verticale de chacun d'eux,
toutes leurs décompositions possibles, la même couleur étant utilisée
pour les deux nombres premiers d'un même couple.
 La disposition "équitable" de N points sur une sphère. Alors que la chose est triviale sur
un cercle, elle est impossible à faire rigoureusement sur la sphère. Seule est possible une méthode reposant sur des essais aléatoires destinés
à améliorer un certain critère.
La disposition "équitable" de N points sur une sphère. Alors que la chose est triviale sur
un cercle, elle est impossible à faire rigoureusement sur la sphère. Seule est possible une méthode reposant sur des essais aléatoires destinés
à améliorer un certain critère.
 Le jeu de la vie de John Conway. Simultanément aux développements des ordinateurs, eurent
lieu des recherches concernant des systèmes abstraits et élémentaires appelés automates. Il s'agit de systèmes de particules résidant en
général sur les nœuds de réseaux carrés et évoluant au cours du temps en suivant des lois de vie et de mort extrémement simples.
En fonction des conditions initiales et des lois exactes utilisées, des systèmes aux comportements étonnants, éventuellement
auto-reproducteurs, peuvent être conçus. Ils montrent clairement que du simple peut émerger le complexe.
Le jeu de la vie de John Conway. Simultanément aux développements des ordinateurs, eurent
lieu des recherches concernant des systèmes abstraits et élémentaires appelés automates. Il s'agit de systèmes de particules résidant en
général sur les nœuds de réseaux carrés et évoluant au cours du temps en suivant des lois de vie et de mort extrémement simples.
En fonction des conditions initiales et des lois exactes utilisées, des systèmes aux comportements étonnants, éventuellement
auto-reproducteurs, peuvent être conçus. Ils montrent clairement que du simple peut émerger le complexe.
 Le système solaire géocentrique.
Même si Aristarque de Samos (~310-230 avant Jésus Christ),
ou encore Hypatie d'Alexandrie (quatrième siècle de notre ère),
avaient tenté
d'imposer sans succès une autre vision, pendant de nombreux siècles notre Terre fut
considérée comme étant le centre du Monde : le Soleil tournait autour et les planètes alors
connues décrivaient dans le ciel de régulières boucles dites de rétrogradation.
C'était le modèle des épicycles de Ptolémée (astronome grec du deuxième siècle de notre ère).
Mais les progrès accomplis en matière d'observation [26]
et de mesure [27]
rendirent cette description de plus en plus difficilement acceptable.
Le système solaire géocentrique.
Même si Aristarque de Samos (~310-230 avant Jésus Christ),
ou encore Hypatie d'Alexandrie (quatrième siècle de notre ère),
avaient tenté
d'imposer sans succès une autre vision, pendant de nombreux siècles notre Terre fut
considérée comme étant le centre du Monde : le Soleil tournait autour et les planètes alors
connues décrivaient dans le ciel de régulières boucles dites de rétrogradation.
C'était le modèle des épicycles de Ptolémée (astronome grec du deuxième siècle de notre ère).
Mais les progrès accomplis en matière d'observation [26]
et de mesure [27]
rendirent cette description de plus en plus difficilement acceptable.
 Le système solaire héliocentrique.
En 1543, une révolution éclata : le moine polonais
Nicolas Copernic [29] mit le Soleil au
centre du système solaire, faisant par la-même de notre Terre une planète
comme les autres. Puis en 1609, Johannes Kepler (Astronomia Nova) décrivit
la trajectoire des planètes [30] par des ellipses
dont l'un des deux foyers était le Soleil.
Enfin, en 1687, Sir Isaac Newton publia ses fameux
Philisophiae Naturalis Principia Mathematica
dans lesquels les lois de la mécanique classique
firent leur apparition [31].
Le système solaire héliocentrique.
En 1543, une révolution éclata : le moine polonais
Nicolas Copernic [29] mit le Soleil au
centre du système solaire, faisant par la-même de notre Terre une planète
comme les autres. Puis en 1609, Johannes Kepler (Astronomia Nova) décrivit
la trajectoire des planètes [30] par des ellipses
dont l'un des deux foyers était le Soleil.
Enfin, en 1687, Sir Isaac Newton publia ses fameux
Philisophiae Naturalis Principia Mathematica
dans lesquels les lois de la mécanique classique
firent leur apparition [31].
 Rajoutons une nouvelle planète dans le système solaire.
Introduisons donc correctement [32]
une nouvelle planète suivant seize trajectoires différentes,
toutes en dehors du plan de l'écliptique.
Rajoutons une nouvelle planète dans le système solaire.
Introduisons donc correctement [32]
une nouvelle planète suivant seize trajectoires différentes,
toutes en dehors du plan de l'écliptique.
 Un système solaire à l'apparence chaotique.
Les astronomes de cette planète observent des trajectoires (apparentes !) très
différentes des épicycles de Ptolémée en particulier par l'absence de périodicités évidentes.
Leur travail aurait certainement été beaucoup plus difficile que celui de Nicolas Copernic !
Un système solaire à l'apparence chaotique.
Les astronomes de cette planète observent des trajectoires (apparentes !) très
différentes des épicycles de Ptolémée en particulier par l'absence de périodicités évidentes.
Leur travail aurait certainement été beaucoup plus difficile que celui de Nicolas Copernic !
 Donnons un exemple d'une telle "monstruosité" : la courbe de von Koch.
D'après ce qui vient d'être dit, il est évident que ces courbes ne peuvent être
tracées exactement car, en effet, sinon cela signifierait l'existence des tangentes.
Seules des approximations peuvent être présentées. Mais cela ne doit pas nous choquer : c'est
aussi le cas dans bien d'autre circonstances et par exemple lorsque l'on montre les premières décimales de pi...
La courbe de von Koch, comme tous les autres "objets" fractals, est définie par
une règle de construction indéfiniment répétée [36]
et c'est seulement à la limite qu'apparaitrait le "monstre" [37].
Cette règle apparait dans les trois cases en bas et à gauche de la figure : elle consiste à
remplacer le tiers central d'un grand segment (00 en bleu) par les deux côtés supérieurs d'un triangle
équilatéral (01 en rouge). Puis cette règle est répétée sur les quatres petits segments (01 en rouges) et encore répétée
indéfiniment sur des segments de plus en plus petits, mais de plus en plus nombreux...
Donnons un exemple d'une telle "monstruosité" : la courbe de von Koch.
D'après ce qui vient d'être dit, il est évident que ces courbes ne peuvent être
tracées exactement car, en effet, sinon cela signifierait l'existence des tangentes.
Seules des approximations peuvent être présentées. Mais cela ne doit pas nous choquer : c'est
aussi le cas dans bien d'autre circonstances et par exemple lorsque l'on montre les premières décimales de pi...
La courbe de von Koch, comme tous les autres "objets" fractals, est définie par
une règle de construction indéfiniment répétée [36]
et c'est seulement à la limite qu'apparaitrait le "monstre" [37].
Cette règle apparait dans les trois cases en bas et à gauche de la figure : elle consiste à
remplacer le tiers central d'un grand segment (00 en bleu) par les deux côtés supérieurs d'un triangle
équilatéral (01 en rouge). Puis cette règle est répétée sur les quatres petits segments (01 en rouges) et encore répétée
indéfiniment sur des segments de plus en plus petits, mais de plus en plus nombreux...
 L'ensemble de Mandelbrot : l'itération d'une transformation élémentaire du second
degré [41] dans le plan complexe conduit à un extraordinaire objet
pour lequel l'autosimilarité est évidente sur les quelques images de ce zoom.
L'ensemble de Mandelbrot : l'itération d'une transformation élémentaire du second
degré [41] dans le plan complexe conduit à un extraordinaire objet
pour lequel l'autosimilarité est évidente sur les quelques images de ce zoom.
 Un agrégat fractal : des petites particules initialement bien rangées
(en bas et àgauche) sont animées d'un mouvement aléatoire. Leur seule propriété utile est d'être
collante. Ainsi au cours du temps, des agrégats de plus en plus gros se forment jusqu'à aboutir à
un unique agrégat fractal (en haut et à droite).
Un agrégat fractal : des petites particules initialement bien rangées
(en bas et àgauche) sont animées d'un mouvement aléatoire. Leur seule propriété utile est d'être
collante. Ainsi au cours du temps, des agrégats de plus en plus gros se forment jusqu'à aboutir à
un unique agrégat fractal (en haut et à droite).
 Les côtes maritimes : suivant le modèle d'Andrea Baldassarri, Andrea Gabrielli et
Bernard Sapoval, la "force" d'attaque de la mer est inversement proportionnelle à la longueur des côtes. Ces dernières n'offrent
pas partout la même résistance. Là où
elles sont friables, il y a érosion, la mer pénètre alors dans les terres, la longueur des côtes augmente et ainsi
la force décroit : un équilibre relatif correspondant à une structure fractale s'établit.
Les côtes maritimes : suivant le modèle d'Andrea Baldassarri, Andrea Gabrielli et
Bernard Sapoval, la "force" d'attaque de la mer est inversement proportionnelle à la longueur des côtes. Ces dernières n'offrent
pas partout la même résistance. Là où
elles sont friables, il y a érosion, la mer pénètre alors dans les terres, la longueur des côtes augmente et ainsi
la force décroit : un équilibre relatif correspondant à une structure fractale s'établit.