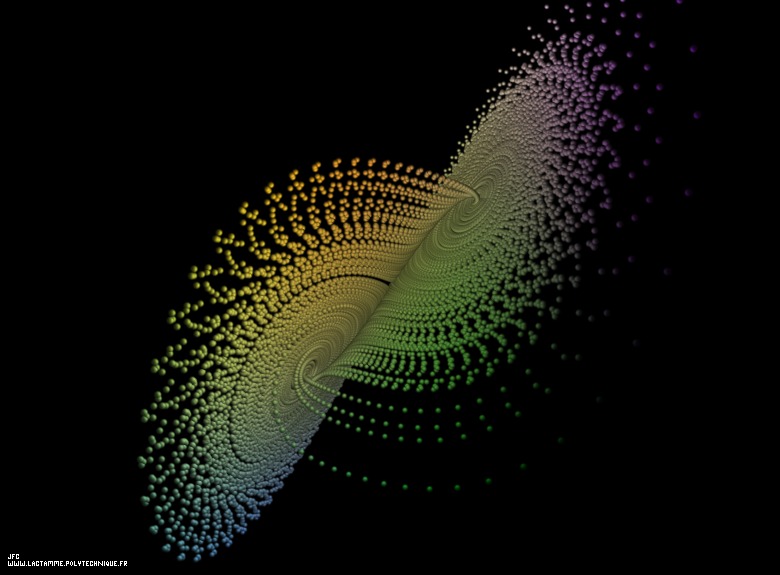
The Lorenz attractor [L'attracteur de Lorenz].
The Lorenz attractor [L'attracteur de Lorenz].
See its rotation.
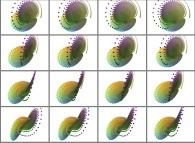See a set of 4x3 stereograms.
- dx
| ---- = -10x + 10y
| dt
|
| dy
< ---- = 28x - y - xz
| dt
|
| dz 8
| ---- = - ---z + xy
- dt 3
This picture is obtained integrating these equations using the Runge-Kutta
method of the fourth order with:
{X ,Y ,Z } = {0.01,0.01,0.01}
0 0 0
Dt = 0.01
each sphere displays a time step and its attributes are chosen as follows:
RADIUS = constant
RED = K.Dx
GREEN = K.Dy
BLUE = K.Dz
where K denotes a renormalization factor and {Dx,Dy,Dz} are the results of
the numerical integration process.
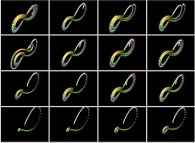sensitivity to initial conditions,
the 
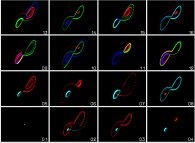sensitivity to integration methods
and the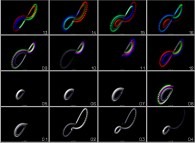 
sensitivity to rounding-off errors.
- dx
| ---- = -10x + 10y
| dt
|
| dy
< ---- = 28x - y - xz
| dt
|
| dz 8
| ---- = - ---z + xy
- dt 3
Cette image présente la trajectoire que décrit le
système au cours du temps dans l'espace
[x,y,z], à partir d'une condition initiale arbitraire ({0.01,0.01,0.01}).
La couleur n'a pas ici qu'une valeur artistique;
elle véhicule une information pertinente: les
intensités des trois couleurs fondamentales
(le Rouge, le Vert et le Bleu) sont
proportionnelles respectivement aux trois
dérivées en t définies ci-dessus.
