Les Triangles d'Or et les Pavages de Penrose non Périodiques du Plan
CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France
[Site Map and Help [Plan du Site et Aide]]
[The Y2K Bug [Le bug de l'an 2000]]
[Are we ready for the Year 2038 [Notre informatique est-elle prête pour l'An 2038] ?]
[Real Numbers don't exist in Computers and Floating Point Computations aren't safe. [Les Nombres Réels n'existent pas dans les Ordinateurs et les Calculs Flottants ne sont pas sûrs.]]
[N'oubliez pas de visiter Une Machine Virtuelle à Explorer l'Espace-Temps et au-delà où vous trouverez plus de 10.000 images et animations à la frontière de l'Art et de la Science]
(Site WWW CMAP28 : cette page a été créée le 08/05/2012 et mise à jour le 08/05/2026 20:16:28 -CEST-)
[in english/en anglais]
Mots-Clefs : Golden Ratio, Nombre d'or, Golden Rectangle, Rectangle d'or, Golden Triangle, Triangle d'or, Plane Non Periodical Tiling, Pavage Non Périodique du Plan, Penrose Tiling, Pavage de Penrose.
Le nombre d'or (phi) est aussi connu que le nombre pi. Il est la solution positive de l'équation du second degré :
2
x = x + 1
et possède la valeur :
___
1 + \/ 5
phi = ----------- ~ 1.6180339887498949
2
Le Rectangle d'Or est un rectangle dont le rapport des côtés est égal à phi.
Il est connu comme étant le rectangle le plus agéable à regarder et il apparait en blanc dans l'image suivante :
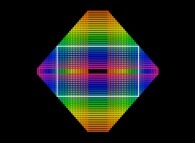
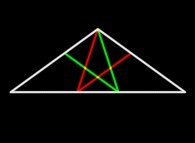
Il est aussi possible de définir deux Triangles d'Or (dits Plat et Mince respectivement).
Ils sont isocèles et le rapport de leurs côtés sont respectivement égaux à phi et à 1/phi.
Ils possèdent une propriété remarquable : il est possible de les découper de deux façons différentes et symétriques
en un certain nombre de triangles plus petits, mais de même nature :
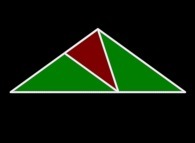
Plat
= 
+ 
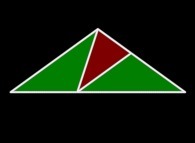Mince
= 
+ 
Ce découpage peut être répété à des échelles de plus en plus petites donnant ainsi naissance à un pavage
non périodique du plan (à l'intérieur du premier triangle, c'est-à-dire le plus grand), en particulier lorsque le choix
entre le découpage rouge et le découpage vert est aléatoire.
Voici un exemple :
En utilisant un choix un peu plus complexe entre les deux découpages, il est possible d'associer systématiquement deux triangles de même nature :
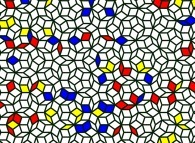
Ensuite, en effaçant le côté commun à chaque paire de triangles ainsi créés, on obtient un pavage non périodique
du plan tel qu'il fut imaginé par Roger Penrose :
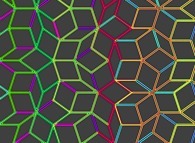
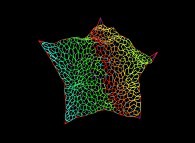
Enfin, il est possible de "jouer" avec ces éléments :
Copyright © Jean-François COLONNA, 2012-2026.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2012-2026.