Ensembles Fractals Déterministes N-Dimensionnels
utilisant les Quaternions, les Octonions et plus
(MandelBulb, JuliaBulbs et au-delà...)
CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[Real Numbers don't exist in Computers and Floating Point Computations aren't safe. [Les Nombres Réels n'existent pas dans les Ordinateurs et les Calculs Flottants ne sont pas sûrs.]]
[N'oubliez pas de visiter Une Machine Virtuelle à Explorer l'Espace-Temps et au-delà où vous trouverez plus de 10.000 images et animations à la frontière de l'Art et de la Science]
(Site WWW CMAP28 : cette page a été créée le 24/12/2009 et mise à jour le 03/10/2024 17:09:57 -CEST-)
[in english/en anglais]
Résumé : Est-il possible d'étendre la complexité des ensembles fractals déterministes bidimensionnels
à des espaces à trois, quatre et huit dimensions ? Que sont le "MandelBulb" et les "JuliaBulb"s ?
Peut-on "mélanger" des ensembles fractals déterministes et non déterministes ?
Les itérations sont fondamentales !
Mots-Clefs : Fractal Geometry, Deterministic Fractal Sets, MandelBulb, JuliaBulb, quaternionic numbers, pseudo-quaternionic numbers, octonionic numbers, pseudo-octonionic numbers.
Plan de ce document :
Remarque preliminaire : Ces ensembles fractals sont dits
déterministes car aucun processus aléatoire
n'intervient mathématiquement parlant (contrairement aux
fractals non déterministes). Malgré tout, leurs calculs sont non linéaires et
sont donc sensibles aux erreurs d'arrondi qui peuvent produire
des artefacts d'apparence aléatoire.
1-ENSEMBLES FRACTALS DETERMINISTES BIDIMENSIONNELS :
Depuis de nombreuses années, les ensembles fractals déterministes bidimensionnels sont bien connus
car ils présentent de magnifiques et mystérieuses structures à toutes les échelles.
Tous ces ensembles sont obtenus en itérant des fonctions (a priori quelconques),
c'est-à-dire en calculant des suites du type :
Z = f(Z )
n+1 n
en chaque point (appelé alors point courant 'C')
d'un domaine (en général rectangulaire) du plan complexe
et ce à partir d'une valeur
Z0 donné (rappelons qu'un nombre complexe est défini comme un couple de nombres réels).
Grâce à l'exemple des ensembles de Julia J(A), nous préciserons
ce que cela signifie dans les lignes suivantes.
La plupart du temps il s'agit de polynômes du second degré donnant ainsi naissance en particulier :
Expliquons dans ce cas particulier ce que signifie itérer.
En chaque point 'C' d'un domaine (en général rectangulaire) du plan complexe,
on regarde comment évolue la suite de points :
Z = C
0
2 2
Z = Z + A = C + A
1 0
2 2 2
Z = Z + A = (C + A) + A
2 1
2 2 2 2
Z = Z + A = ((C + A) + A) + A
3 2
2 2 2 2 2
Z = Z + A = (((C + A) + A) + A) + A
4 3
etc...
Deux possibilités se rencontrent alors : ou bien cette suite de points s'éloigne
indéfiniment (et sans retour possible), ou bien elle reste au voisinage de l'origine et l'on dit alors
que le point 'C' appartient à l'ensemble de Julia J(A).
On notera que le nombre d'iterations effectuables en chaque point 'C' est limité pour des
raisons matérielles évidentes et lorsque son maximum (fixé arbitrairement,
par exemple à 1000) est atteint, l'appartenance est aussi décrétée
(voir quelques remarques concernant la notion de
nombre d'iterations et les difficultés inhérentes à ces calculs).
Voici la visualisation de quelques itérations lors du calcul
de l'ensemble de Mandelbrot  et d'un ensemble de Julia
et d'un ensemble de Julia  .
.
N'importe quelle fonction peut être utilisée
et par exemple la fonction Zêta de Riemann  ,
mais les polynômes du second degré sont déjà très instructifs tout en étant les plus simples.
,
mais les polynômes du second degré sont déjà très instructifs tout en étant les plus simples.
Comment passer ensuite des itérations aux images ?
Les couleurs de chaque points peuvent être choisies en fonction du nombre n+1 d'itérations
effectuées ou (cas des seize ensembles de Julia précédents)
encore de l'argument (le 'thêta' dans les lignes suivantes)
du dernier Z(n+1) calculé (cas de l'ensemble de Mandelbrot ci-dessus). Une visualisation
tridimensionnelle peut-être aussi réalisée en utilisant
le nombre n+1 d'itérations comme une troisième dimension  .
Mais évidemment cela n'introduit aucune structures fractales réellement tridimensionnelles
(voir quelques remarques concernant le coloriage des objets fractals)...
.
Mais évidemment cela n'introduit aucune structures fractales réellement tridimensionnelles
(voir quelques remarques concernant le coloriage des objets fractals)...
2-ENSEMBLES FRACTALS DETERMINISTES QUADRIDIMENSIONNELS ET OCTODIMENSIONNELS :
Les nombres réels peuvent être considérés comme
les étiquettes des points de la droite et
les nombres complexes comme celles des points du plan.
Un nombre complexe est un couple (ensemble ordonné) de nombres réels.
Pendant de nombreuses années les mathématiciens ont cherché de nouveaux nombres qui pourraient
étiqueter les points de l'espace tridimensionnel : leur quête n'aboutit pas
à cause de l'impossibilité de définir de façon cohérente leur produit
(malheureuse dépendance linéaire des trois hypothétiques
vecteurs de base {1,i,j}).
William Hamilton découvrit que cela pouvait être fait en "sautant" dans la quatrième dimension :
les quaternions étaient nés et définis comme un couple de nombres complexes,
c'est-à-dire aussi comme un quadruplet de nombres réels
(au passage, l'étape suivante est la huitième dimension : les octonions...).
Afin de généraliser dans l'espace les magnifiques et mystérieuses structures des ensembles fractals
dans le plan complexe, ce fut donc une idée naturelle, pour tout ceux (dont je suis...) qui
travaillèrent sur ce sujet que d'utiliser les quaternions et les octonions.
Effectivement, cela fut fait, mais les résultats furent malheureusement relativement
décevants : par exemple,
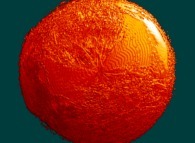
une section tridimensionnelle à l'intérieur de l'ensemble de Mandelbrot
dans les quaternions  montre une forte symétrie de rotation et ne présente aucune structure réellement tridimensionnelle
à tous les niveaux comme espéré ainsi que le révèle ce zoom
montre une forte symétrie de rotation et ne présente aucune structure réellement tridimensionnelle
à tous les niveaux comme espéré ainsi que le révèle ce zoom  .
.
3-"VRAIS" ENSEMBLES FRACTALS DETERMINISTES QUADRIDIMENSIONNELS ET OCTODIMENSIONNELS :
Rappelons l'arithmétique des nombres complexes. L'addition ('+') de deux nombres complexes
{x1,y1} et {x2,y2} est définie par :
z +z = {x ,y }+{x ,y } = {x +x ,y +y }
1 2 1 1 2 2 1 2 1 2
La multiplication ('*') est un peu plus compliquée :
z *z = {x ,y }*{x ,y } = {x *x - y *y ,x *y + x *y }
1 2 1 1 2 2 1 2 1 2 1 2 2 1
(même s'il s'agit d'une aberration mathématique, des définitions plus compliquées peuvent être expérimentées)
Si les coordonnées polaires sont utilisées à la place des coordonnées cartésiennes
('R' and 'T' signifiant 'Rho' et 'Thêta' respectivement),
cela est beaucoup plus simple :
{R ,T }*{R ,T } = {R *R ,T +T }
1 1 2 2 1 2 1 2
avec :
x = R *cos(T )
i i i
y = R *sin(T )
i i i
En particulier, le carré d'un nombre complexe vaut alors :
2 2
(R,T) = (R ,2*T)
Au cours des années passées, Daniel White a eu l'excellente idée d'étendre ce processus
dans l'espace tridimensionnel. Des triplets (ensembles ordonnés) de nombres réels (x,y,z) sont alors définis,
ainsi que leur addition et leur multiplication comme suit :
{x ,y ,z }+{x ,y ,z } = {x +x ,y +y ,z +z }
1 1 1 2 2 2 1 2 1 2 1 2
{R ,T ,P }*{R ,T ,P } = {R *R ,T +T ,P +P }
1 1 1 2 2 2 1 2 1 2 1 2
avec :
x = R *cos(P )*sin(T )
i i i i
y = R *sin(P )*sin(T )
i i i i
z = R *cos(T )
i i i
('R', 'T' and 'P' étant les trois coordonnées sphériques 'Rho', 'Thêta' et 'Phi' respectivement).
En particulier, la puissance n-ième d'un tel triplet vaut alors :
n n
(R,T,P) = (R ,n*T,n*P)
formule qui est à la base de la plupart des images alors obtenues.
J'ai généralisé cette idée dans des espaces à quatre et huit dimensions pour les raisons suivantes :
- Tout ce que j'avait fait pour les quaternions et les octonions
pouvait être réutilisé ; il suffisait
d'introduire la définition d'une nouvelle multiplication et d'ajouter
un indicateur logique permettant à cette dernière de remplacer
la multiplication usuelle lors des calculs.
- Des espaces à quatre et à huit dimensions incluent des espaces à deux et à trois dimensions.
- Enfin, cela ouvre la porte à des métamorphoses. Pour comprendre aisément
cela, il suffit de revenir à l'espace tridimensionnel. Dans celui-ci il est
possible de faire des coupes planes dans un objet quelconque et par exemple dans un cylindre ;
suivant l'orientation du plan, la coupe se métamorphosera : un cercle,
une ellipse ou encore un rectangle. Cela sera illustré par la suite avec
un ensemble de Julia.
Nota : par soucis de simplicité, ce processus sera décrit dans un espace à quatre
dimensions. Dans un espace à huit dimensions, les formules sont plus compliquées
et utilisent 3+4=7 angles 'Ai' (au lieu de 3), l'indice 'i' variant de 1 à 7.
Cette nouvelle multiplication (appelée simplement
multiplication par la suite) est définie par :
{R ,T ,P ,A }*{R ,T ,P ,A } = {fR(R ,R ),fT(T ,T ),fP(P ,P ),fA(A ,A )}
1 1 1 1 2 2 2 2 1 2 1 2 1 2 1 2
'R', 'T', 'P' et 'A' étant les quatre coordonnées hypersphériques 'Rho', 'Thêta', 'Phi' et 'Alpha' respectivement :
x = R *cos(P )*sin(T )*sin(A )
i i i i i
y = R *sin(P )*sin(T )*sin(A )
i i i i i
z = R *cos(T )*sin(A )
i i i i
t = R *cos(A )
i i i
et les quatre fonctions arbitraires (comme cela sera illustré plus loin)
'fR', 'fT', 'fP' et 'fA' étant définies par défaut avec :
fR(R ,R ) = R * R
1 2 1 2
fT(T ,T ) = T + T
1 2 1 2
fP(P ,P ) = P + P
1 2 1 2
fA(A ,A ) = A + A
1 2 1 2
afin d'être compatibles avec la multiplication dans le plan complexe et avec les résultats
de Daniel White.
Cela donne alors naissance aux pseudo-quaternions pour lesquels,
en toute généralité, la multiplication, comme pour les quaternions
d'Hamilton, n'est pas commutative (l'ordre dans lequel les multiplications seront effectuées
aura de l'importance, sauf évidemment d'une part dans le cas particulier où les quatre fonctions
'fR', 'fT', 'fP' et 'fA' commutent et d'autre part lors du simple calcul d'une puissance...).
Avec mes définitions, la multiplication est le processus de base, alors que
l'élévation à une puissance entière d'un nombre (par
exemple le calcul de son carré ou de son cube)
n'est qu'un processus secondaire puisque le résultat de plusieurs multiplications successives.
Il convient de noter alors que pour calculer le polynôme 'qn' ('q' étant un pseudo-quaternion)
deux solutions sont disponibles : soit utiliser le fait que qn=q...q ('q' est multiplié n-1 fois
par lui-même) en utilisant les définitions précédentes des quatre fonctions.
Dans ce cas, la multiplication est effectuée n-1 fois. L'autre possibilité
consiste à calculer le polynôme '1.q' ("'1' multiplié par 'q'") avec les définitions suivantes pour
les quatre fonctions :
n
fR(R ,R ) = (R * R )
1 2 1 2
fT(T ,T ) = n*(T + T )
1 2 1 2
fP(P ,P ) = n*(P + P )
1 2 1 2
fA(A ,A ) = n*(A + A )
1 2 1 2
soit dans le cas particulier du polynôme '1.q' :
n
fR(1,R) = R
fT(0,T) = n*T
fP(0,P) = n*P
fA(0,A) = n*A
La multiplication n'est alors effectuée qu'une seule fois (dans ce cas particulier, les deux
possibilité donnent évidemment le même résultat). Mais l'intérêt de privilgégier
la multiplication par rapport à l'élévation à une puissance entière réside dans le fait qu'il est ainsi
possible de générer des objets reposant sur l'itération de fonctions plus générales
que les polynômes de type 'qn' et faisant appel, par exemple, à des divisions.
Pour Daniel White, l'élévation à une puissance entière est un processus de base et ses fonctions
équivalentes ne sont appliquées qu'une seule fois. Cela peut conduire à des résultats très différents !
Il est notable d'ajouter que tous ces programmes sont inclus dans un environnement qui
permet la redéfinition dynamique des opérations arithmétiques élémentaires utilisées
[Plus d'informations]
ajoutant ainsi encore plus de flexibilité et de possibilités.
Voici quelques exemples avec les notations suivantes :
- 'q' (=(x,y,z,t)=(R,T,P,A)) représente un pseudo-quaternion,
- 'qA' et 'qC' sont respectivement un pseudo-quaternion paramètre et le point courant,
- un polynôme 'P' du premier degré s'écrit 'P(q) = 1*q + ...' afin de forcer une multiplication.
-
 :
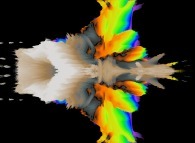
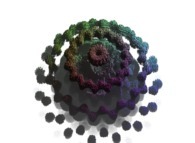
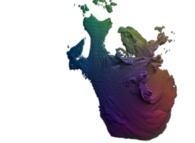
Cet ensemble de Mandelbrot est une section tridimensionnelle
(utilisant l'hyperplan t=0) et a été calculé en utilisant
un polynôme 'P' du premier degré et les quatre fonctions suivantes :
:
Cet ensemble de Mandelbrot est une section tridimensionnelle
(utilisant l'hyperplan t=0) et a été calculé en utilisant
un polynôme 'P' du premier degré et les quatre fonctions suivantes :
P(q) = 1*q + q
C
2
fR(R ,R ) = (R *R )
1 2 1 2
fT(T ,T ) = 2*(T +T )
1 2 1 2
fP(P ,P ) = 2*(P +P )
1 2 1 2
fA(A ,A ) = 2*(A +A )
1 2 1 2
-

 :
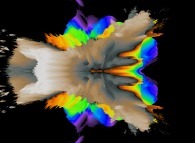
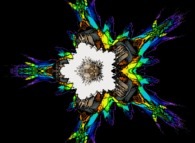
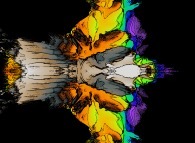
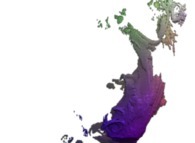
Cet ensemble de Mandelbrot est une section tridimensionnelle
(utilisant l'hyperplan t=0.1) et a été calculé en utilisant
un polynôme 'P' du second degré et les quatre fonctions suivantes :
:
Cet ensemble de Mandelbrot est une section tridimensionnelle
(utilisant l'hyperplan t=0.1) et a été calculé en utilisant
un polynôme 'P' du second degré et les quatre fonctions suivantes :
2
P(q) = q + q
C
fR(R ,R ) = R *R
1 2 1 2
fT(T ,T ) = 2*(T +T ) + pi
1 2 1 2
fP(P ,P ) = 2*(P +P ) + pi
1 2 1 2
fA(A ,A ) = A +A
1 2 1 2
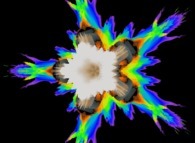
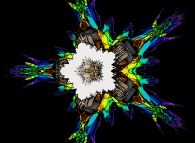
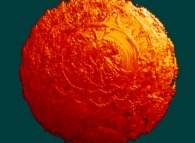
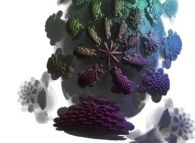
Sa vue d'avion  ressemble à un flocon de neige
avec 5 branches. Il a été calculé à l'aide d'un polynôme 'P' du second degré.
Pour des polynômes du troisième, quatrième, cinquième et sixième degré,
les nombres de branches sont respectivement
13 (=5*2+3),
29 (=13*2+3),
61 (=29*2+3) et
125 (=61*2+3).
ressemble à un flocon de neige
avec 5 branches. Il a été calculé à l'aide d'un polynôme 'P' du second degré.
Pour des polynômes du troisième, quatrième, cinquième et sixième degré,
les nombres de branches sont respectivement
13 (=5*2+3),
29 (=13*2+3),
61 (=29*2+3) et
125 (=61*2+3).
-
 :
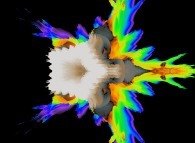
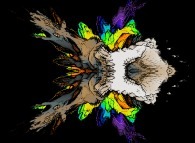
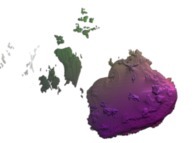
Cet ensemble de Mandelbrot est une section tridimensionnelle
(utilisant l'hyperplan t=0) et a été calculé en utilisant
un polynôme 'P' du huitième degré et les quatre fonctions suivantes :
:
Cet ensemble de Mandelbrot est une section tridimensionnelle
(utilisant l'hyperplan t=0) et a été calculé en utilisant
un polynôme 'P' du huitième degré et les quatre fonctions suivantes :
8
P(q) = q + q
C
fR(R ,R ) = R *R
1 2 1 2
fT(T ,T ) = 1*(T +T ) + pi
1 2 1 2
fP(P ,P ) = 2*(P +P ) + pi
1 2 1 2
fA(A ,A ) = A +A
1 2 1 2
-
 :
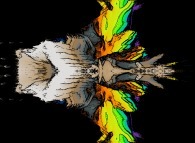
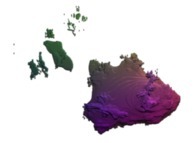
Cet ensemble de Mandelbrot est une section tridimensionnelle
(utilisant l'hyperplan t=0) et a été calculé en utilisant
un polynôme 'P' du second degré et les quatre fonctions suivantes :
:
Cet ensemble de Mandelbrot est une section tridimensionnelle
(utilisant l'hyperplan t=0) et a été calculé en utilisant
un polynôme 'P' du second degré et les quatre fonctions suivantes :
2
P(q) = q + q
C
fR(R ,R ) = R *R
1 2 1 2
fT(T ,T ) = 1*(T +T ) + pi
1 2 1 2
fP(P ,P ) = 2*(P +P ) + pi
1 2 1 2
fA(A ,A ) = A +A
1 2 1 2
-
 :
Cet ensemble de Mandelbrot est une section tridimensionnelle
(utilisant l'hyperplan t=0) et a été calculé en utilisant
un polynôme 'P' du premier degré et les quatre fonctions suivantes :
:
Cet ensemble de Mandelbrot est une section tridimensionnelle
(utilisant l'hyperplan t=0) et a été calculé en utilisant
un polynôme 'P' du premier degré et les quatre fonctions suivantes :
P(q) = 1*q + q
C
8
fR(R ,R ) = (R *R )
1 2 1 2
fT(T ,T ) = 8*(T +T )
1 2 1 2
fP(P ,P ) = 8*(P +P )
1 2 1 2
fA(A ,A ) = 8*(A +A )
1 2 1 2
-
 :
Cet ensemble de Mandelbrot est une section tridimensionnelle
(utilisant l'hyperplan t=0.7) et a été calculé en utilisant
un polynôme 'P' du premier degré et les quatre fonctions suivantes :
:
Cet ensemble de Mandelbrot est une section tridimensionnelle
(utilisant l'hyperplan t=0.7) et a été calculé en utilisant
un polynôme 'P' du premier degré et les quatre fonctions suivantes :
P(q) = 1*q + q
C
8
fR(R ,R ) = (R *R )
1 2 1 2
fT(T ,T ) = 8*(T +T )
1 2 1 2
fP(P ,P ) = 8*(P +P )
1 2 1 2
fA(A ,A ) = 8*(A +A )
1 2 1 2
-
 :
Cet ensemble de Julia est une section tridimensionnelle
(utilisant l'hyperplan t=0) et a été calculé en utilisant
un polynôme 'P' du second degré et les quatre fonctions suivantes :
:
Cet ensemble de Julia est une section tridimensionnelle
(utilisant l'hyperplan t=0) et a été calculé en utilisant
un polynôme 'P' du second degré et les quatre fonctions suivantes :
2
P(q) = q + {-0.5815147625160462,+0.6358885017421603,0,0}
fR(R ,R ) = R *R
1 2 1 2
fT(T ,T ) = T +T
1 2 1 2
fP(P ,P ) = P +P
1 2 1 2
fA(A ,A ) = A +A
1 2 1 2
-
 :
Cet ensemble de Julia est une section tridimensionnelle
(utilisant l'hyperplan t=0) et a été calculé en utilisant
un polynôme 'P' du premier degré et les quatre fonctions suivantes :
:
Cet ensemble de Julia est une section tridimensionnelle
(utilisant l'hyperplan t=0) et a été calculé en utilisant
un polynôme 'P' du premier degré et les quatre fonctions suivantes :
P(q) = 1*q + {-0.5815147625160462,+0.6358885017421603,0,0}
3
fR(R ,R ) = (R *R )
1 2 1 2
fT(T ,T ) = 3*(T +T )
1 2 1 2
fP(P ,P ) = 3*(P +P )
1 2 1 2
fA(A ,A ) = A +A
1 2 1 2
-
 :
Cet ensemble de Julia est une section tridimensionnelle
et a été calculé en utilisant
un polynôme 'P' du premier degré et les quatre fonctions suivantes
('Fractal(x,y,z,t)' est une foncion fractale non déterministe à valeur
dans [2,12] du type de celles qui sont utilisees pour
générer et animer des montagnes et des nuages) :
:
Cet ensemble de Julia est une section tridimensionnelle
et a été calculé en utilisant
un polynôme 'P' du premier degré et les quatre fonctions suivantes
('Fractal(x,y,z,t)' est une foncion fractale non déterministe à valeur
dans [2,12] du type de celles qui sont utilisees pour
générer et animer des montagnes et des nuages) :
P(q) = 1*q + {0,1,0,0}
Fractal(x,y,z,t)
fR(R ,R ) = (R *R )
1 2 1 2
fT(T ,T ) = 5*(T +T )
1 2 1 2
fP(P ,P ) = 8*(P +P )
1 2 1 2
fA(A ,A ) = 11*(A +A )
1 2 1 2
Ceci est un mélange original entre les fractals déterministes et les fractals non déterministes.
-
 :
Cet ensemble de Julia est une section tridimensionnelle
et a été calculé en utilisant
un polynôme 'P' du premier degré et les quatre fonctions suivantes
('Fractal(x,y,z,t)' est une foncion fractale non déterministe à valeur
dans [2,12] du type de celles qui sont utilisees pour
générer et animer des montagnes et des nuages) :
:
Cet ensemble de Julia est une section tridimensionnelle
et a été calculé en utilisant
un polynôme 'P' du premier degré et les quatre fonctions suivantes
('Fractal(x,y,z,t)' est une foncion fractale non déterministe à valeur
dans [2,12] du type de celles qui sont utilisees pour
générer et animer des montagnes et des nuages) :
P(q) = 1*q + {0,1,0,0}
Fractal(x,y,z,t)
fR(R ,R ) = (R *R )
1 2 1 2
fT(T ,T ) = Fractal(x,y,z,t)*(T +T )
1 2 1 2
fP(P ,P ) = Fractal(x,y,z,t)*(P +P )
1 2 1 2
fA(A ,A ) = Fractal(x,y,z,t)*(A +A )
1 2 1 2
Ceci est un mélange original entre les fractals déterministes et les fractals non déterministes.
-
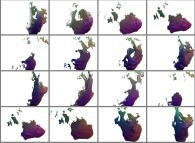
 :
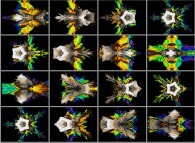
Cette métamorphose faite de seize images est obtenue par une rotation dans l'espace
quadridimensionnel de la section tridimensionnelle dans un ensemble de Julia
calculé en utilisant
un polynôme 'P' du premier degré et les quatre fonctions suivantes :
:
Cette métamorphose faite de seize images est obtenue par une rotation dans l'espace
quadridimensionnel de la section tridimensionnelle dans un ensemble de Julia
calculé en utilisant
un polynôme 'P' du premier degré et les quatre fonctions suivantes :
P(q) = 1*q + {-0.5815147625160462,+0.6358885017421603,0,0}
2
fR(R ,R ) = (R *R )
1 2 1 2
fT(T ,T ) = 2*(T +T )
1 2 1 2
fP(P ,P ) = 2*(P +P )
1 2 1 2
fA(A ,A ) = 2*(A +A )
1 2 1 2
-
 :
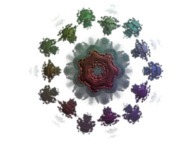
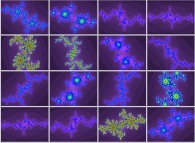
Cette métamorphose faite de seize images est obtenue par une rotation dans l'espace
quadridimensionnel de la section tridimensionnelle dans un ensemble de Julia
calculé en utilisant
un polynôme 'P' du troisième degré et les quatre fonctions suivantes :
:
Cette métamorphose faite de seize images est obtenue par une rotation dans l'espace
quadridimensionnel de la section tridimensionnelle dans un ensemble de Julia
calculé en utilisant
un polynôme 'P' du troisième degré et les quatre fonctions suivantes :
2 3
P(q) = 1*q - q + q + {-0.5815147625160462,+0.6358885017421603,0,0}
2
fR(R ,R ) = (R *R )
1 2 1 2
fT(T ,T ) = 2*(T +T )
1 2 1 2
fP(P ,P ) = 2*(P +P )
1 2 1 2
fA(A ,A ) = 2*(A +A )
1 2 1 2
4-LES ITERATIONS SONT FONDAMENTALES :
Ces "expériences" montrent une nouvelle fois que la notion d'itération est fondamentale
en permettant, à partir de règles en général élémentaires, d'aller du simple vers le complexe.
Cela se voit par exemple dans l'étude des
automates cellulaires ou encore dans celle de la
marche aléatoire.
Cette nouvelle famille de fractales N-dimensionnelles vient le confirmer.
5.1-MandelBulbs :
[Plus d'ensembles de Mandelbrot dans les pseudo-quaternions]
[Plus d'ensembles de Mandelbrot dans les pseudo-octonions]
5.2-JuliaBulbs :
[Plus d'ensembles de Julia dans les pseudo-quaternions]
[Plus d'ensembles de Julia dans les pseudo-octonions]
5.3-Ensembles Divers :
[Plus d'ensembles divers dans les pseudo-quaternions]
[Plus d'ensembles divers dans les pseudo-octonions]
Copyright © Jean-François COLONNA, 2009-2024.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2009-2024.


 et d'un ensemble de Julia
et d'un ensemble de Julia  .
.
 ,
mais les polynômes du second degré sont déjà très instructifs tout en étant les plus simples.
,
mais les polynômes du second degré sont déjà très instructifs tout en étant les plus simples.
 .
Mais évidemment cela n'introduit aucune structures fractales réellement tridimensionnelles
(voir quelques remarques concernant le coloriage des objets fractals)...
.
Mais évidemment cela n'introduit aucune structures fractales réellement tridimensionnelles
(voir quelques remarques concernant le coloriage des objets fractals)...
 montre une forte symétrie de rotation et ne présente aucune structure réellement tridimensionnelle
à tous les niveaux comme espéré ainsi que le révèle ce zoom
montre une forte symétrie de rotation et ne présente aucune structure réellement tridimensionnelle
à tous les niveaux comme espéré ainsi que le révèle ce zoom  .
.