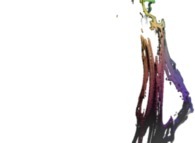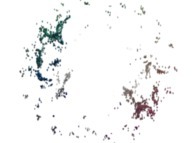-
 :
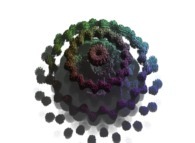
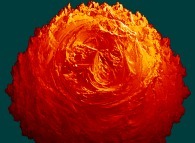
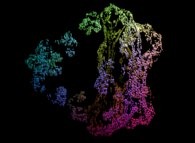
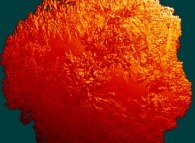
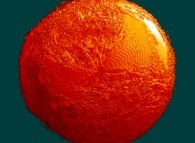
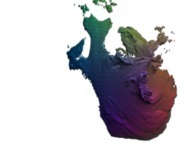
this Mandelbrot set is a tridimensional cross-section
(using the t=0 hyperplane) and was computed with
a polynomial 'P' of the first degree and the following four functions:
:
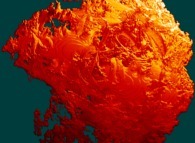
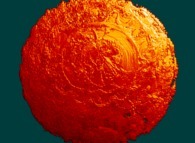
this Mandelbrot set is a tridimensional cross-section
(using the t=0 hyperplane) and was computed with
a polynomial 'P' of the first degree and the following four functions:
P(q) = 1*q + q
C
2
fR(R ,R ) = (R *R )
1 2 1 2
fT(T ,T ) = 2*(T +T )
1 2 1 2
fP(P ,P ) = 2*(P +P )
1 2 1 2
fA(A ,A ) = 2*(A +A )
1 2 1 2
-

 :
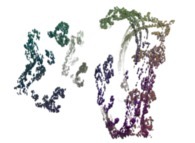
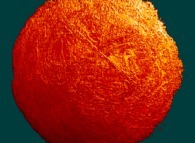
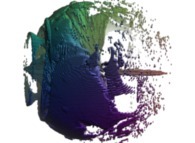
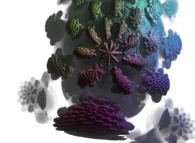
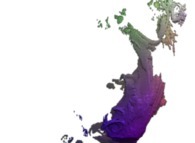
this Mandelbrot set is a tridimensional cross-section
(using the t=0.1 hyperplane) and was computed with
a polynomial 'P' of the second degree and the following four functions:
:
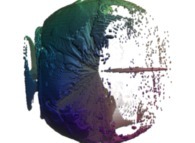
this Mandelbrot set is a tridimensional cross-section
(using the t=0.1 hyperplane) and was computed with
a polynomial 'P' of the second degree and the following four functions:
2
P(q) = q + q
C
fR(R ,R ) = R *R
1 2 1 2
fT(T ,T ) = 2*(T +T ) + pi
1 2 1 2
fP(P ,P ) = 2*(P +P ) + pi
1 2 1 2
fA(A ,A ) = A +A
1 2 1 2
Its bird's-eye view  looks like a snow flake
with 5 spikes. It was computed using a polynomial 'P' of the second degree.
For polynomials of the third, fourth, fifth and sixth degree,
the numbers of spikes are
13 (=5*2+3),
29 (=13*2+3),
61 (=29*2+3) and
125 (=61*2+3) respectively.
looks like a snow flake
with 5 spikes. It was computed using a polynomial 'P' of the second degree.
For polynomials of the third, fourth, fifth and sixth degree,
the numbers of spikes are
13 (=5*2+3),
29 (=13*2+3),
61 (=29*2+3) and
125 (=61*2+3) respectively.
-
 :
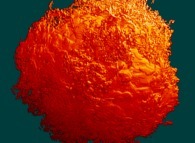
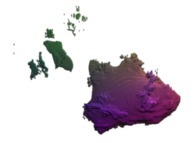
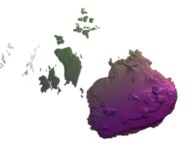
this Mandelbrot set is a tridimensional cross-section
(using the t=0 hyperplane) and was computed with
a polynomial 'P' of the eighth degree and the following four functions:
:
this Mandelbrot set is a tridimensional cross-section
(using the t=0 hyperplane) and was computed with
a polynomial 'P' of the eighth degree and the following four functions:
8
P(q) = q + q
C
fR(R ,R ) = R *R
1 2 1 2
fT(T ,T ) = 1*(T +T ) + pi
1 2 1 2
fP(P ,P ) = 2*(P +P ) + pi
1 2 1 2
fA(A ,A ) = A +A
1 2 1 2
-
 :
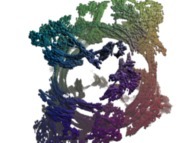
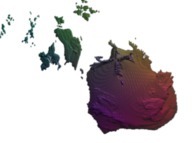
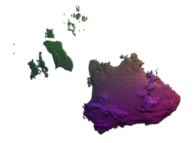
this Mandelbrot set is a tridimensional cross-section
(using the t=0 hyperplane) and was computed with
a polynomial 'P' of the second degree and the following four functions:
:
this Mandelbrot set is a tridimensional cross-section
(using the t=0 hyperplane) and was computed with
a polynomial 'P' of the second degree and the following four functions:
2
P(q) = q + q
C
fR(R ,R ) = R *R
1 2 1 2
fT(T ,T ) = 1*(T +T ) + pi
1 2 1 2
fP(P ,P ) = 2*(P +P ) + pi
1 2 1 2
fA(A ,A ) = A +A
1 2 1 2
-
 :
this Mandelbrot set is a tridimensional cross-section
(using the t=0 hyperplane) and was computed with
a polynomial 'P' of the first degree and the following four functions:
:
this Mandelbrot set is a tridimensional cross-section
(using the t=0 hyperplane) and was computed with
a polynomial 'P' of the first degree and the following four functions:
P(q) = 1*q + q
C
8
fR(R ,R ) = (R *R )
1 2 1 2
fT(T ,T ) = 8*(T +T )
1 2 1 2
fP(P ,P ) = 8*(P +P )
1 2 1 2
fA(A ,A ) = 8*(A +A )
1 2 1 2
-
 :
this Mandelbrot set is a tridimensional cross-section
(using the t=0.7 hyperplane) and was computed with
a polynomial 'P' of the first degree and the following four functions:
:
this Mandelbrot set is a tridimensional cross-section
(using the t=0.7 hyperplane) and was computed with
a polynomial 'P' of the first degree and the following four functions:
P(q) = 1*q + q
C
8
fR(R ,R ) = (R *R )
1 2 1 2
fT(T ,T ) = 8*(T +T )
1 2 1 2
fP(P ,P ) = 8*(P +P )
1 2 1 2
fA(A ,A ) = 8*(A +A )
1 2 1 2
-
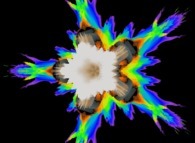
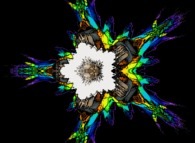
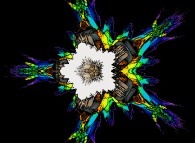
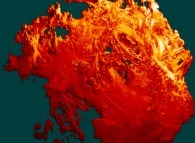
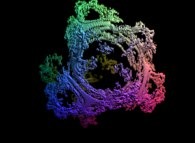
 :
this Julia set is a tridimensional cross-section
(using the t=0 hyperplane) and was computed with
a polynomial 'P' of the second degree and the following four functions:
:
this Julia set is a tridimensional cross-section
(using the t=0 hyperplane) and was computed with
a polynomial 'P' of the second degree and the following four functions:
2
P(q) = q + {-0.5815147625160462,+0.6358885017421603,0,0}
fR(R ,R ) = R *R
1 2 1 2
fT(T ,T ) = T +T
1 2 1 2
fP(P ,P ) = P +P
1 2 1 2
fA(A ,A ) = A +A
1 2 1 2
-
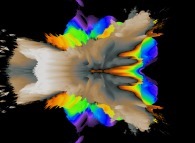
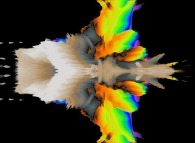
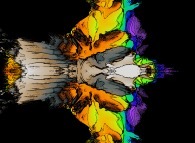
 :
this Julia set is a tridimensional cross-section
(using the t=0 hyperplane) and was computed with
a polynomial 'P' of the first degree and the following four functions:
:
this Julia set is a tridimensional cross-section
(using the t=0 hyperplane) and was computed with
a polynomial 'P' of the first degree and the following four functions:
P(q) = 1*q + {-0.5815147625160462,+0.6358885017421603,0,0}
3
fR(R ,R ) = (R *R )
1 2 1 2
fT(T ,T ) = 3*(T +T )
1 2 1 2
fP(P ,P ) = 3*(P +P )
1 2 1 2
fA(A ,A ) = A +A
1 2 1 2
-
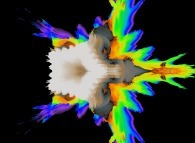
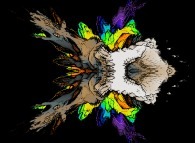
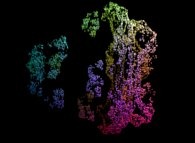
 :
this Julia set is a tridimensional cross-section
and was computed with
a polynomial 'P' of the first degree and the following four functions
('Fractal(x,y,z,t)' is a non deterministic fractal function with value
inside [2,12] identical to the ones that are used
to generate and animate mountains and clouds):
:
this Julia set is a tridimensional cross-section
and was computed with
a polynomial 'P' of the first degree and the following four functions
('Fractal(x,y,z,t)' is a non deterministic fractal function with value
inside [2,12] identical to the ones that are used
to generate and animate mountains and clouds):
P(q) = 1*q + {0,1,0,0}
Fractal(x,y,z,t)
fR(R ,R ) = (R *R )
1 2 1 2
fT(T ,T ) = 5*(T +T )
1 2 1 2
fP(P ,P ) = 8*(P +P )
1 2 1 2
fA(A ,A ) = 11*(A +A )
1 2 1 2
It is an original mixing between deterministic and non deterministic fractals.
-
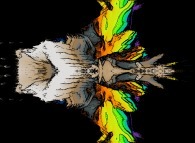
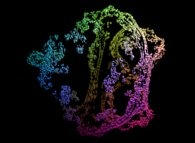
 :
this Julia set is a tridimensional cross-section
and was computed with
a polynomial 'P' of the first degree and the following four functions
('Fractal(x,y,z,t)' is a non deterministic fractal function with value
inside [2,12] identical to the ones that are used
to generate and animate mountains and clouds):
:
this Julia set is a tridimensional cross-section
and was computed with
a polynomial 'P' of the first degree and the following four functions
('Fractal(x,y,z,t)' is a non deterministic fractal function with value
inside [2,12] identical to the ones that are used
to generate and animate mountains and clouds):
P(q) = 1*q + {0,1,0,0}
Fractal(x,y,z,t)
fR(R ,R ) = (R *R )
1 2 1 2
fT(T ,T ) = Fractal(x,y,z,t)*(T +T )
1 2 1 2
fP(P ,P ) = Fractal(x,y,z,t)*(P +P )
1 2 1 2
fA(A ,A ) = Fractal(x,y,z,t)*(A +A )
1 2 1 2
It is an original mixing between deterministic and non deterministic fractals.
-
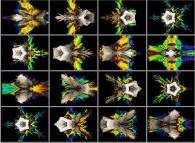
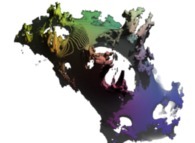
 :
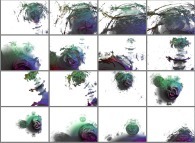
This metamorphosis made of sixteen pictures is obtained using a rotation
in the quadridimensional space of the tridimensional cross-section
inside a Julia set computed with
a polynomial 'P' of the first degree and the following four functions:
:
This metamorphosis made of sixteen pictures is obtained using a rotation
in the quadridimensional space of the tridimensional cross-section
inside a Julia set computed with
a polynomial 'P' of the first degree and the following four functions:
P(q) = 1*q + {-0.5815147625160462,+0.6358885017421603,0,0}
2
fR(R ,R ) = (R *R )
1 2 1 2
fT(T ,T ) = 2*(T +T )
1 2 1 2
fP(P ,P ) = 2*(P +P )
1 2 1 2
fA(A ,A ) = 2*(A +A )
1 2 1 2
-
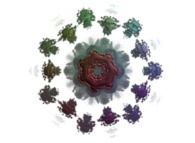
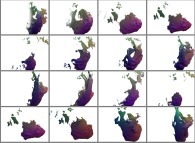
 :
This metamorphosis made of sixteen pictures is obtained using a rotation
in the quadridimensional space of the tridimensional cross-section
inside a Julia set computed with
a polynomial 'P' of the third degree and the following four functions:
:
This metamorphosis made of sixteen pictures is obtained using a rotation
in the quadridimensional space of the tridimensional cross-section
inside a Julia set computed with
a polynomial 'P' of the third degree and the following four functions:
2 3
P(q) = 1*q - q + q + {-0.5815147625160462,+0.6358885017421603,0,0}
2
fR(R ,R ) = (R *R )
1 2 1 2
fT(T ,T ) = 2*(T +T )
1 2 1 2
fP(P ,P ) = 2*(P +P )
1 2 1 2
fA(A ,A ) = 2*(A +A )
1 2 1 2


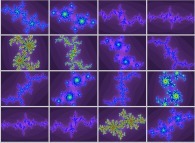
 and of a Julia set
and of a Julia set  .
.
 .
.
 .
.
 exhibits a high symmetry and no tridimensional structures at all levels as expected
as can be seen with this zooming in
exhibits a high symmetry and no tridimensional structures at all levels as expected
as can be seen with this zooming in  .
.