From Monodimensional Binary Cellular Automata
to
Monodimensional "Quasi-Continuous" Cellular Automata,
(Random) Perturbations of Cellular Automata
Jean-François COLONNA
jean-francois.colonna@polytechnique.edu
CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, 91120 Palaiseau, France
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[Do you believe that Real Numbers exist for a computer and that floating point computations are safe? [Croyez-vous que les Nombres Réels existent dans un ordinateur et que les calculs flottants sont sûrs?]]
[Please, visit A Virtual Machine for Exploring Space-Time and Beyond, the place where you can find thousands of pictures and animations between Art and Science]
(CMAP28 WWW site: this page was created on 11/26/2008 and last updated on 06/19/2023 14:18:19 -CEST-)
[en français/in french]
Abstract: How to generalize the monodimensional binary cellular automaton?
Keywords: Picture Synthesis,
Monodimensional Binary Cellular Automata,
Monodimensional Quasi-Continuous Cellular Automata,
Automates Cellulaires Binaires Monodimensionnels,
Automates Cellulaires Quasi-Continus Monodimensionnels,
Random Perturbations of Cellular Automata,
Perturbations Aleatoires d'Automates Cellulaires.
Contents of this page:
1-MONODIMENSIONAL BINARY CELLULAR AUTOMATA:
An elementary monodimensional binary cellular automaton is a monodimensional set of cells.
At time 't', each cell (with coordinate 'x') has a value 'CELL(x,t)'
that equals either 0 (Black) or 1 (White)
and has two neighbours (one at its left 'CELL(x-1,t)'
and one at its right 'CELL(x+1,t)').
Regarding the points outside the picture (at left and at right),
their value can be set arbitrarly (White or Black)
or again the monodimensional space can be defined as periodical.
The time evolution of this set of cells is defined by means of 8 rules.
BBB = B/W
BBW = B/W
BWB = B/W
BWW = B/W
WBB = B/W
WBW = B/W
WWB = B/W
WWW = B/W
where "B/W" means Black or White.
For example, the fourth rule "BWW = B/W" means:
if ((CELL(x-1,t)==Black)&&(CELL(x,t)==White)&&(CELL(x+1,t)==White)) then CELL(x,t+1)=Black or White
The right hand side of the 8 rules suffices to define a monodimensional binary cellular automaton.
Then there are 2^8=256 different monodimensional binary cellular automata.
Each one can be labelled using a binary code; for example here is the following automaton:
BBB = W (=1)
BBW = B (=0)
BWB = W (=1)
BWW = B (=0)
WBB = B (=0)
WBW = W (=1)
WWB = B (=0)
WWW = W (=1)
Then the right-hand sides of the 8 preceding rules are concatenated:
-------- --------
WBWBBWBW = 10100101 = 01011010
The binary number 01101110 equals the decimal number 90 (for 90=64+16+8+2).
Then this monodimensional binary cellular automaton is dubbed the automaton number 90.
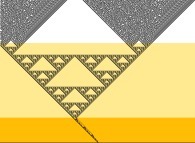
Here are some monodimensional binary cellular automata with various initial conditions
(one single White point -left column- and 49 periodical White points -right column-):
-
automaton number 86,
-
automaton number 90,
-
automaton number 106,
-
automaton number 110,
-
automaton number 184.
-
the 256 automata.
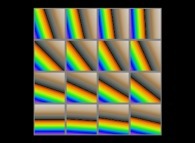
Here are some more examples where more than one automaton are used:
2-MONODIMENSIONAL "QUASI-CONTINUOUS" CELLULAR AUTOMATA:
A monodimensional binary cellular automaton can be viewed as the following tridimensional object:
WWB=B/W-------------WWW=B/W
/. /|
/ . / |
/ . / |
/ . / |
/ . / |
WBB=B/W-------------WBW=B/W |
| . | |
| . | |
| . | |
| BWB=B/W..........|..BWW=B/W
| . | /
| . | /
^ | . | /
Y | Z | . | /
| / |. |/
|/ BBB=B/W-------------BBW=B/W
O---->
X
that can be simplified into:
B/W-----------------B/W
/. /|
/ . / |
/ . / |
/ . / |
/ . / |
B/W-----------------B/W |
| . | |
| . | |
| . | |
| B/W............|....B/W
| . | /
| . | /
^ | . | /
Y | Z | . | /
| / |. |/
|/ B/W-----------------B/W
O---->
X
the 'X', 'Y' and 'Z' axes being respectively the 'Right', 'Left' and 'Current' axes.
To become "quasi-continuous" ("quasi" for a computer does not know what continuity is...),
it suffices to fill the preceding cube using some interpolation or any other process.
Here are some monodimensional "quasi-continuous" cellular automata.
The left column, the middle column and the right column display respectively
cross-sections inside the defining cube, the initial conditions (only the bottom line is used) and
the resulting picture.
-
*
= 
-
*
= 
-
*
= 
-
*
= 
-
*
= 
-
*
= 
-
*
= 
Here are some more examples where more than one automaton are used:
3-(RANDOM) PERTURBATIONS OF CELLULAR AUTOMATA:
At time 't', each cell (with coordinate 'x') has a value 'CELL(x,t)'.
Instead of using its two neighbours (the one at its left 'CELL(x-1,t)'
and the one at its right 'CELL(x+1,t)'),
from time to time (with a given probability) two random values can be used.
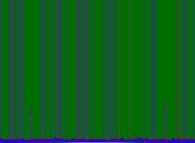
Here are some examples:
-
*
= 
probability=0.0004
-
*
= 
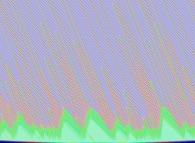
probability=0.1
Copyright © Jean-François Colonna, 2008-2023.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2008-2023.
