Définition et Animation de Variétés Bi- et Tridimensionnelles
au Moyen de Pseudo-Projections,
Auto-Transformations d'Images
CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France
france telecom, France Telecom R&D
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[Real Numbers don't exist in Computers and Floating Point Computations aren't safe. [Les Nombres Réels n'existent pas dans les Ordinateurs et les Calculs Flottants ne sont pas sûrs.]]
[N'oubliez pas de visiter Une Machine Virtuelle à Explorer l'Espace-Temps et au-delà où vous trouverez plus de 10.000 images et animations à la frontière de l'Art et de la Science]
(Site WWW CMAP28 : cette page a été créée le 24/12/2004 et mise à jour le 03/10/2024 17:10:39 -CEST-)
[in english/en anglais]
Résumé : Les surfaces tridimensionnelles -les variétés bidimensionnelles- peuvent être définies à l'aide de trois matrices
et donc à l'aide de trois images monochromes -ou d'une image couleur-.
Une dynamique arbitraire pour une surface tridimensionnelle pourra alors être définie par une animation.
Ceci peut être généralisé à des dimensions supérieures et utilisé pour définir des procédures d'auto-transformation d'images.
Mots-Clefs : Holographic Principle, Pseudo-Projection, Tridimensional Surfaces, Bidimensional Manifolds, Tridimensional Manifolds, Picture Self-Transformations.
Plan de ce document :
1-NOTION D'IMAGE :
Une image en noir et blanc (dite monochrome) est définie
comme un tableau rectangulaire (ou matrice) de points (ou pixels).
Chaque point y est codé par une valeur numérique dont les plus
petite et plus grande valeurs possibles
représentent le noir et le blanc respectivement.
En général il s'agit de nombres entiers entre 0 et 255, mais
des nombres réels (par exemple entre -1 et +1) peuvent être aussi utilisés
afin de disposer d'une meilleure précision (cela sera le cas dans les calculs
présentés ci-après).
Nos rétines contiennent deux types de capteur : les bâtonnets (sensibles à
l'intensité lumineuse) et trois types de cônes (sensibles respectivement à
trois couleurs primaires : le rouge, le vert et le bleu).
Une image en couleur sera donc définie,
selon les principes de la synthèse dite additive, comme
l'union de trois images monochromes correspondant chacune à l'une des trois couleurs
primaires.
2-SURFACES TRIDIMENSIONNELLES (VARIETES BIDIMENSIONNELLES) :
De nombreuses surfaces -variétés bidimensionnelles- dans un espace tridimensionnel
peuvent être définies à l'aide d'un ensemble de trois équations :
X = Fx(u,v)
Y = Fy(u,v)
Z = Fz(u,v)
avec :
u ∈ [Umin,Umax]
v ∈ [Vmin,Vmax]
Par exemple :
Fx(u,v) = R.sin(u).cos(v)
Fy(u,v) = R.sin(u).sin(v)
Fz(u,v) = R.cos(u)
avec :
u ∈ [0,pi]
v ∈ [0,2.pi]
définit une sphère de rayon R centrée à l'origine.
[Umin,Umax]*[Vmin,Vmax] définit alors un domaine bidimensionnel rectangulaire D.
v ^
|
V |...... ---------------------------
max | |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
V |...... ---------------------------
min | : :
| : :
O------------------------------------------------->
U U u
min max
Si D est echantillonné grâce à une grille rectangulaire bidimensionnelle (faite de Nu*Nv points),
les trois coordonnées {X,Y,Z} peuvent être définies à l'aide de trois matrices rectangulaires :
X = Mx(i,j)
Y = My(i,j)
Z = Mz(i,j)
avec :
i = f(u,Umin,Umax,Nu)
j = g(v,Vmin,Vmax,Nv)
où 'f' et 'g' désignent deux fonctions linéaires triviales...
Il est alors possible de définir une surface tridimensionnelle -une variété bidimensionnelle-
à l'aide de trois matrices.
Une image noir et blanc étant une matrice, une surface tridimensionnelle
pourra être définie grâce à trois images noir et blanc c'est-à-dire
grâce à une image en couleurs :
en quelque sorte,
un principe holographique. Cela permettra en particulier de faire avec
les surfaces tout ce qui est possible avec les images (filtrages, déformations,
interpolations, opérations arithmétiques,...).
Précisons cela grâce à l'exemple de la sphère. Voici les trois matrices
Mx, My et Mz (l'échelle de gris utilisée visualisant des valeurs variant entre -1 et 1) :
- Mx(i,j) =
 = Fx(u,v) = sin(u).cos(v)
= Fx(u,v) = sin(u).cos(v)
- My(i,j) =
 = Fy(u,v) = sin(u).sin(v)
= Fy(u,v) = sin(u).sin(v)
- Mz(i,j) =
 = Fz(u,v) = cos(u)
= Fz(u,v) = cos(u)
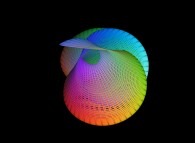
La superposition "additive" (rouge+vert+bleu)
des trois matrices (images noir et blanc) donne l'image en couleurs suivante :
 +
+  +
+  =
= 
qui est l'image en couleurs associée à la sphère (sa pseudo-projection).
Les niveaux respectifs de rouge, de vert et de bleu au point {i,j}
donnent les coordonnées tridimensionnelles {Fx(u,v),Fy(u,v),Fz(u,v)}
d'un point de cette sphère.
Evidemment, les trois matrices "superposées" ne définissent que les coordonnées
d'un nombre fini de points. Les coordonnées
des autres points sont obtenues par des interpolations utilisant des points voisins et définis.
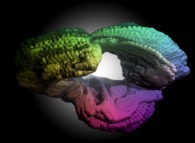
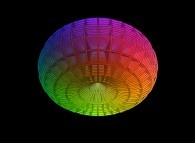
La sphère est alors représentable par un ensemble "dense" de points et pour visualiser
un maillage en longitude-latitude, il suffit de ne pas visualiser tous les points
:
-
 ==
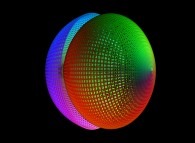
== 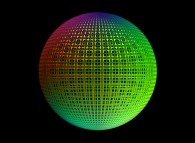 une sphère.
une sphère.
-
 ==
== 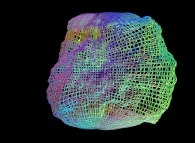 une sphère "froissée" (un "bruit" fractal a été ajouté aux coordonnées {X,Y,Z}).
une sphère "froissée" (un "bruit" fractal a été ajouté aux coordonnées {X,Y,Z}).
-
 ==
==  une sphère "froissée" (un "bruit" fractal a été ajouté à la coordonnée radiale).
une sphère "froissée" (un "bruit" fractal a été ajouté à la coordonnée radiale).
Les couleurs des surfaces sont évidemment arbitraires. Mais pour l'ensemble des exemples
ici présentés, ce sont les gradients des trois fonctions Fx, Fy et Fz
qui définissent les trois composantes Rouge, Vert et Bleue.
Il convient de noter qu'utiliser la pseudo-projection elle-même
pour colorier la surface est de peu d'intérêt ; en effet, les composantes
{Rouge,Verte,Bleue} seraient alors proportionnelles aux coordonneés
{X,Y,Z} respectivement, ce qui donnerait donc tout simplement des dégradés
(par exemple, un dégradé de rouge parallèle à
l'axe des abscisses ainsi qu'il est possible de le vérifier
à l'aide de la bouteille de Klein).
Voici de nombreux autres exemples :
-
 ==
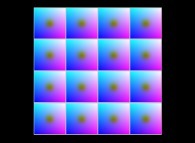
==  un plan.
un plan.
-
 ==
== 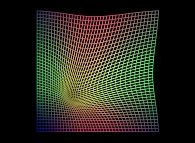 un plan distordu.
un plan distordu.
-
 ==
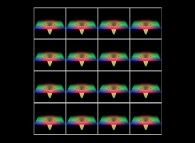
== 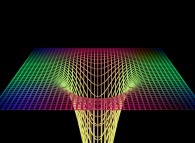 un "plan pseudo-gaussien".
un "plan pseudo-gaussien".
-
 ==
== 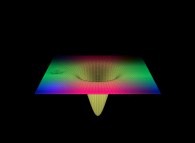 un "plan pseudo-bi-gaussien".
un "plan pseudo-bi-gaussien".
-
 ==
== 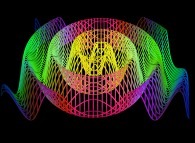 un "plan spiralant".
un "plan spiralant".
-
 ==
==  un "plan fractal" de Peano.
un "plan fractal" de Peano.
-
 ==
==  un "plan fractal" avec surplombs.
un "plan fractal" avec surplombs.
-
 ==
==  un "plan fractal" avec surplombs.
un "plan fractal" avec surplombs.
-
 ==
== 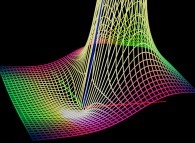 le relief -module- de la fonction exp(1/z).
le relief -module- de la fonction exp(1/z).
-
 ==
== 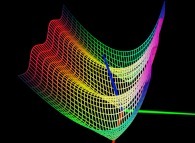 le relief -module- de la fonction sin(z).
le relief -module- de la fonction sin(z).
-
 ==
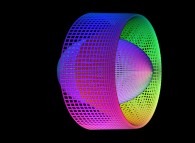
==  un cylindre "froissé" (un "bruit" fractal a été ajouté).
un cylindre "froissé" (un "bruit" fractal a été ajouté).
-
 ==
== 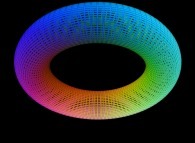 un tore.
un tore.
-
 ==
==  un tore "froissé" (un "bruit" fractal a été ajouté).
un tore "froissé" (un "bruit" fractal a été ajouté).
-
 ==
==  un tore "froissé" (un "bruit" fractal a été ajouté).
un tore "froissé" (un "bruit" fractal a été ajouté).
-
 ==
==  la seconde 'puissance' d'un tore.
la seconde 'puissance' d'un tore.
-
 ==
==  la troisième 'puissance' d'un tore.
la troisième 'puissance' d'un tore.
-
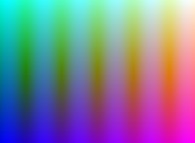 ==
==  le module de la fonction sinus complexe.
le module de la fonction sinus complexe.
-
 ==
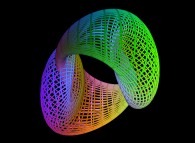
== 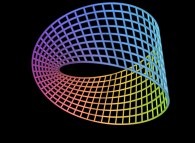 le ruban de Möbius.
le ruban de Möbius.
-
 ==
==  la bouteille de Klein.
la bouteille de Klein.
-
 ==
==  la bouteille de Klein (en utilisant comme couleurs la
pseudo-projection elle-même).
la bouteille de Klein (en utilisant comme couleurs la
pseudo-projection elle-même).
-
 ==
== 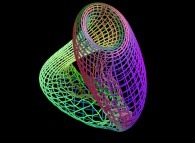 une bouteille de Klein "froissée" (un "bruit" fractal a été ajouté).
une bouteille de Klein "froissée" (un "bruit" fractal a été ajouté).
-
 ==
== 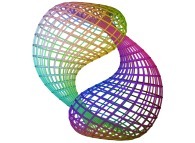 la double bouteille de Jeener.
la double bouteille de Jeener.
-
 ==
== 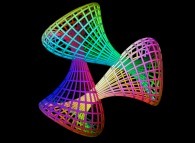 la triple bouteille de Jeener-Klein.
la triple bouteille de Jeener-Klein.
-
 ==
== 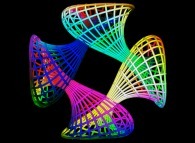 la quadruple bouteille bilatère de Jeener.
la quadruple bouteille bilatère de Jeener.
-
 ==
== 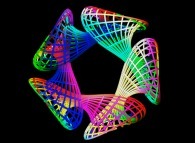 la quintuple bouteille de Jeener-Klein.
la quintuple bouteille de Jeener-Klein.
-
 ==
== 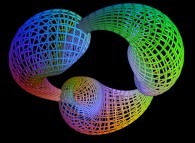 la triple bouteille de Bonan-Jeener-Klein.
la triple bouteille de Bonan-Jeener-Klein.
-
 ==
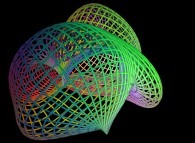
==  un coquillage (surface de Jeener 1).
un coquillage (surface de Jeener 1).
-
 ==
==  un bulot de Jeener 'froissé'.
un bulot de Jeener 'froissé'.
-
 ==
==  un bulot de Jeener 'froissé'.
un bulot de Jeener 'froissé'.
-
 ==
== 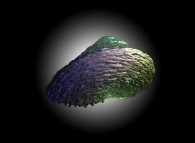 un bulot de Jeener 'froissé'.
un bulot de Jeener 'froissé'.
-
 ==
==  la surface de Boy.
la surface de Boy.
-
 ==
== 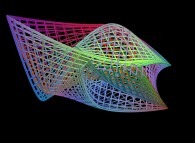 une surface fractale (deux itérations).
une surface fractale (deux itérations).
-
 ==
== 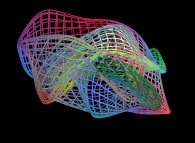 une surface fractale (trois itérations).
une surface fractale (trois itérations).
-
 ==
== 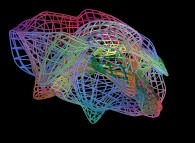 une surface fractale (quatre itérations).
une surface fractale (quatre itérations).
-
 ==
==  une surface fractale (cinq itérations).
une surface fractale (cinq itérations).
-
 ==
== 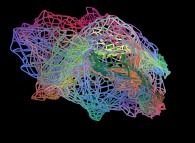 une surface fractale (six itérations).
une surface fractale (six itérations).
-
 ==
== 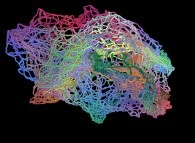 une surface fractale (nombreuses itérations...).
une surface fractale (nombreuses itérations...).
3-COMBINAISON ET MELANGE DE SURFACES TRIDIMENSIONNELLES (VARIETES BIDIMENSIONNELLES) :
Il est facile de combiner et de mélanger des surfaces par l'intermédiaire des images en couleurs qui leur sont associées.
Voici quelques exemples :
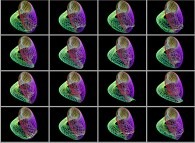
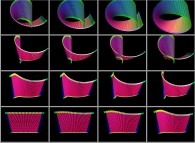
4-ANIMATION DE SURFACES TRIDIMENSIONNELLES (VARIETES BIDIMENSIONNELLES) :
Ainsi, une surface tridimensionnelle peut être définie grâce à une image en couleurs.
Une dynamique arbitraire d'une surface tridimensionnelle pourra alors être
définie par un ensemble d'images en couleurs, c'est-à-dire par une animation en couleurs.
Voici quelques exemples :
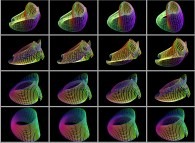
Enfin, il est évident
qu'un ensemble de surfaces tridimensionnelles pourra être définie
par la juxtaposition de plusieurs images en couleurs ou encore
par un ensemble d'images en couleurs -c'est-à-dire par une animation en couleurs-.
Voici quelques exemples :
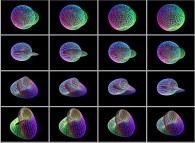
Des trous et des distorsions des coordonnées 'u' et 'v' peuvent être introduits comme sur ces exemples :
-
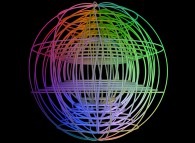 un ensemble de sphères vrillées.
un ensemble de sphères vrillées.
-
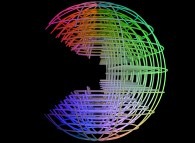 un ensemble de sphères avec des trous.
un ensemble de sphères avec des trous.
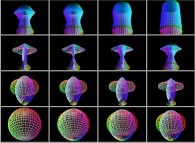
Enfin, ce processus facilite l'interpolation entre surfaces comme sur cet exemple :
-
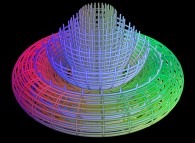 d'un tore à un cylindre.
d'un tore à un cylindre.
5-VARIETES TRIDIMENSIONNELLES :
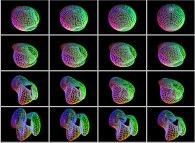
Ceci peut être étendu à des variétés tridimensionnelles. Ainsi :
De nombreuses variétés tridimensionnelles dans un espace tridimensionnel
peuvent être définies à l'aide d'un ensemble de trois équations :
X = Fx(u,v,w)
Y = Fy(u,v,w)
Z = Fz(u,v,w)
avec :
u ∈ [Umin,Umax]
v ∈ [Vmin,Vmax]
w ∈ [Wmin,Wmax]
[Umin,Umax]*[Vmin,Vmax]*[Wmin,Wmax] définit alors un domaine tridimensionnel rectangulaire D.
Si D est echantillonné grâce à une grille rectangulaire tridimensionnelle (faite de Nu*Nv*Nw points),
les trois coordonnées {X,Y,Z} peuvent être définies à l'aide d'un ensemble de Nw triplets de matrices rectangulaires :
X = {Mxk(i,j)}
Y = {Myk(i,j)}
Z = {Mzk(i,j)}
avec :
i = f(u,Umin,Umax,Nu)
j = g(v,Vmin,Vmax,Nv)
k = g(w,Wmin,Wmax,Nw)
où 'f', 'g' et 'h' désignent deux fonctions linéaires triviales...
Il est alors possible de définir une variété tridimensionnelle à l'aide
d'un ensemble de Nw triplets de matrices.
Il est intéressant de rappeler qu'une animation est un ensemble de N images en couleurs
et qu'ainsi, une variete
tridimensionnelle peut être définie grâce à une animation (arbitraire) en couleurs...
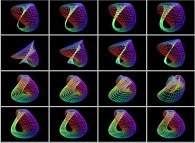
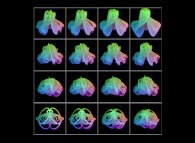
Voici quelques exemples :
-
 ==
== 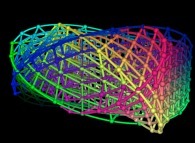 une variéte torique torsadée tridimensionnelle.
une variéte torique torsadée tridimensionnelle.
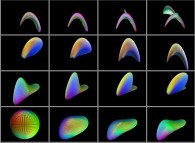
-
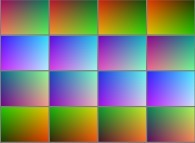 ==
== 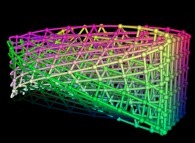 une variété "à la Möbius" tridimensionnelle.
une variété "à la Möbius" tridimensionnelle.
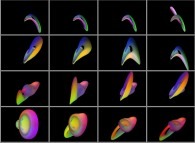
-
 ==
== 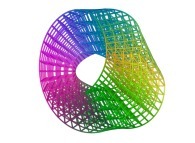 une variété tridimensionnelle de Jeener-Möbius.
une variété tridimensionnelle de Jeener-Möbius.
-
 ==
== 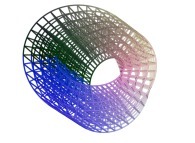 une variété tridimensionnelle de Jeener-Möbius.
une variété tridimensionnelle de Jeener-Möbius.
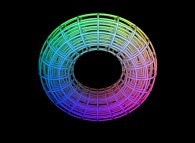
-
 ==
==  un réseau tridimensionnel.
un réseau tridimensionnel.
-
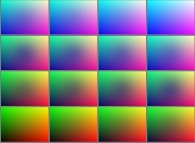 ==
==  un réseau tridimensionnel distordu.
un réseau tridimensionnel distordu.
-
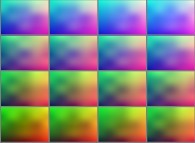 ==
==  une variété fractale tridimensionnelle.
une variété fractale tridimensionnelle.
-
 ==
==  une variété tridimensionnelle définie au moyen d' une interpolation entre la triple bouteille de Bonan-Jeener-Klein et une "double sphère".
une variété tridimensionnelle définie au moyen d' une interpolation entre la triple bouteille de Bonan-Jeener-Klein et une "double sphère".
6-AUTO-TRANSFORMATIONS D'IMAGES :
Ainsi, n'importe quelle image en couleurs peut être utilisée pour définir une surface.
De plus, cette image (vue comme une texture) peut être "mappée" sur sa surface associée
(en utilisant les coordonnées {u,v} comme les coordonnées cartésiennes de la texture).
Il est préférable de symétriser cette texture afin
d'éviter des discontinuités dans le cas des surfaces fermés.
Par exemple, la sphère  est définie par l'image suivante :
est définie par l'image suivante :  comme cela fut décrit précédemment. Apres sa symétrisation, cela donne naissance
à la texture dite canonique de la sphère :
comme cela fut décrit précédemment. Apres sa symétrisation, cela donne naissance
à la texture dite canonique de la sphère :  .
Cette image-texture est distordue durant le "mapping" ;
ce processus est appellé auto-transformation
de l'image initiale :
.
Cette image-texture est distordue durant le "mapping" ;
ce processus est appellé auto-transformation
de l'image initiale :  .
.
Voici le processus utilisé :
X = Fx(u,v)
Y = Fy(u,v)
Z = Fz(u,v)
Les coordonnées tridimensionnelles {X,Y,Z} sont ensuite projetées :
Xp= ProjectionX(X,Y,Z)
Yp= ProjectionY(X,Y,Z)
La distorsion est alors définie par :
DISTORSION(u,v) = TEXTURE(Xp,Yp )
'TEXTURE' étant l'image "texture" à auto-transformer.
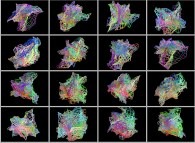
Voici quelques exemples d'auto-transformations d'images sans présenter les surfaces associées :
-
 =>
=> 
-
 =>
=> 
-
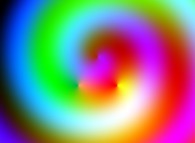 =>
=> 
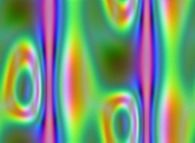
-
 =>
=> 
-
 =>
=> 
-
 =>
=> 
-
 =>
=>  (dans cet exemple, un filtrage de Fourier a été appliqué à l'image initiale afin de la lisser
).
(dans cet exemple, un filtrage de Fourier a été appliqué à l'image initiale afin de la lisser
).
Ce procédé peut être appliqué à des animations en couleurs donnant ainsi naissance à de
complexes animations de textures.
Voici quelques exemples :
Copyright © Jean-François COLONNA, 2004-2024.
Copyright © France Telecom R&D and CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2004-2024.




 +
+  +
+  =
= 




























































































































































































 .
Cette image-texture est distordue durant le "mapping" ;
ce processus est appellé auto-transformation
de l'image initiale :
.
Cette image-texture est distordue durant le "mapping" ;
ce processus est appellé auto-transformation
de l'image initiale :  .
.













