A 'crumpled' torus defined by means of three bidimensional fields [Un tore 'froissé' défini à l'aide de trois champs bidimensionnels].




Many surfaces -bidimensional manifolds- in a tridimensional space can be defined using a set of three equations: 
                    X = Fx(u,v)

                    Y = Fy(u,v)

                    Z = Fz(u,v)
with: 
                    u ∈ [Umin,Umax]

                    v ∈ [Vmin,Vmax]
[Umin,Umax]*[Vmin,Vmax] then defined a bidimensional rectangular domain D. 
                       v ^
                         |
                    V    |...... ---------------------------
                     max |      |+++++++++++++++++++++++++++|
                         |      |+++++++++++++++++++++++++++|
                         |      |+++++++++++++++++++++++++++|
                         |      |+++++++++++++++++++++++++++|
                         |      |+++++++++++++++++++++++++++|
                         |      |+++++++++++++++++++++++++++|
                         |      |+++++++++++++++++++++++++++|
                         |      |+++++++++++++++++++++++++++|
                         |      |+++++++++++++++++++++++++++|
                    V    |...... ---------------------------
                     min |      :                           :
                         |      :                           :
                         O------------------------------------------------->
                                U                           U              u
                                 min                         max

If D is sampled by means of a bidimensional rectangular grid (made of Nu*Nv points), the three {X,Y,Z} coordinates can be defined by means of three rectangular matrices: 
                    X = Mx(i,j)

                    Y = My(i,j)

                    Z = Mz(i,j)
with: 
                    i = f(u,Umin,Umax,Nu)

                    j = g(v,Vmin,Vmax,Nv)
where 'f' and 'g' denote two obvious linear functions...


[for more information about this process]
[Plus d'informations sur ce processus]


For the 'crumpled' torus, the three {X,Y,Z} fields/matrices are as follows:

with 'fractal(u,v)' denoting a bidimensional periodical fractal generator (fractal(u,v) ∈ [1-0.5,1+0.5]).
The same one was used () for the 'X', 'Y' and 'Z' coordinates.


See a related picture:




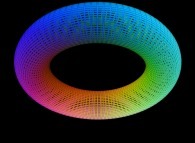See the perfect torus.


(CMAP28 WWW site: this page was created on 03/31/2021 and last updated on 04/16/2023 20:52:06 -CEST-)



[More information about that kind of picture and/or process [Plus d'informations sur ce type d'image et/ou de processus]]


[See the generator of this picture [Voir le générateur de cette image]]

[See all related pictures (including this one) [Voir toutes les images associées (incluant celle-ci)]]

[Please visit the related GeneralitiesVisualization picture gallery [Visitez la galerie d'images GeneralitiesVisualization associée]]

[Go back to AVirtualMachineForExploringSpaceTimeAndBeyond [Retour à AVirtualMachineForExploringSpaceTimeAndBeyond]]

[The Y2K Bug [Le bug de l'an 2000]]

[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[Mail [Courrier]]
[About Pictures and Animations [A Propos des Images et des Animations]]


Copyright © Jean-François Colonna, 2021-2023.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2021-2023.