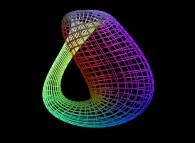
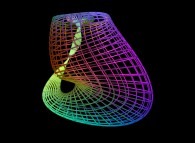
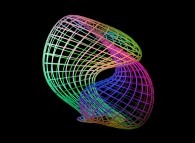
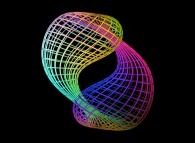
An interpolation between the Klein bottle and the double Jeener bottle defined by means of three sets of bidimensional fields [Une interpolation entre la bouteille de Klein et la double bouteille de Jeener définie à l'aide de trois ensembles de champs bidimensionnels].

                    X = Fx(u,v)

                    Y = Fy(u,v)

                    Z = Fz(u,v)

                    u ∈ [Umin,Umax]

                    v ∈ [Vmin,Vmax]

                       v ^
                         |
                    V    |...... ---------------------------
                     max |      |+++++++++++++++++++++++++++|
                         |      |+++++++++++++++++++++++++++|
                         |      |+++++++++++++++++++++++++++|
                         |      |+++++++++++++++++++++++++++|
                         |      |+++++++++++++++++++++++++++|
                         |      |+++++++++++++++++++++++++++|
                         |      |+++++++++++++++++++++++++++|
                         |      |+++++++++++++++++++++++++++|
                         |      |+++++++++++++++++++++++++++|
                    V    |...... ---------------------------
                     min |      :                           :
                         |      :                           :
                         O------------------------------------------------->
                                U                           U              u
                                 min                         max

                    X = Mx(i,j)

                    Y = My(i,j)

                    Z = Mz(i,j)

                    i = f(u,Umin,Umax,Nu)

                    j = g(v,Vmin,Vmax,Nv)

• Fx
• Fy
• Fz