A Quoi Servent les Mathématiques ?
CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France
france telecom, France Telecom R&D
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[Real Numbers don't exist in Computers and Floating Point Computations aren't safe. [Les Nombres Réels n'existent pas dans les Ordinateurs et les Calculs Flottants ne sont pas sûrs.]]
[N'oubliez pas de visiter Une Machine Virtuelle à Explorer l'Espace-Temps et au-delà où vous trouverez plus de 10.000 images et animations à la frontière de l'Art et de la Science]
(Site WWW CMAP28 : cette page a été créée le 23/10/2000 et mise à jour le 03/10/2024 17:00:34 -CEST-)
(Texte Texte d'une conférence présentée à l'occasion de la Fête de la Science, Ministère de la Recherche, 20/10/2000)
Résumé : A côté des Mathématiques Pures, a priori
éloignées des problèmes concrets, figurent les Mathématiques Appliquées
qui cherchent à résoudre des problèmes posés
tant par la recherche fondamentale que par la recherche
industrielle.
Mots-Clefs :
Anaglyphes,
Art et Science,
Autostéréogrammes,
Chaos Déterministe,
Création Artistique,
Entrelacs,
Erreurs d'arrondi,
Expérimentation Virtuelle,
Génie Logiciel,
Géométrie Fractale,
Infographie,
Mathématiques,
Mécanique Céleste,
Mécanique Quantique,
Physique,
Sensibilité aux Erreurs d'Arrondi,
Simulation Numérique,
Stéréogrammes,
Synthèse de Phénomènes Naturels,
Synthèse de Texture,
Visualisation Scientifique,
Voyage Virtuel dans l'Espace-Temps.
1-Quelques souvenirs personnels :
J'ai toujours aimé les Mathématiques,
sans que jamais, au collège comme au lycée,
ne me soient presentées leurs dimensions tant historique
qu'utilitaire. Cette lacune subsiste encore aujourd'hui dans
nos établissements scolaires, voire universitaires, et c'est
pourquoi il est tout à fait compréhensible que certains ne s'y
intéressent pas, même s'ils présentent de bonnes
dispositions pour celles-ci.
2-Les Mathématiques Pures contre les Mathématiques Appliquées :
Il est de tradition de faire une distinction entre
les Mathématiques dites Pures
et celles qui sont qualifiées d'Appliquées.
Mais cette opposition signifie-t-elle que les premières,
celles qui donc ne sont donc pas appliquées, sont
non applicables et par la-même inutiles ?
Sous-entend-elle de plus que les secondes,
celles qui sont appliquées par définition, sont impures ?
3-Les Mathématiques Pures :
Même si leurs racines, dont les traces remontent à plusieurs milliers d'années
sont constituées de problèmes bien concrets (par exemple,
ceux de partages de biens entre des héritiers),
les Mathématiques Pures trouvent aujourd'hui généralement
leurs source d'inspiration dans des questions
posées de temps en temps par les plus grands mathématiciens.
Ces questions se concrétisent bien souvent sous la forme
de conjectures (c'est-à-dire
de théorèmes non encore démontrés mais qui semblent
vrais).
Ainsi la conjecture de Riemann (relative
aux zéros non triviaux de la
fonction Zêta)
est certainement l'un des plus importants problèmes "ouverts" actuels.
Il y a quelques années, l'un de ceux qui fit
couler le plus d'encre vit son épilogue : il s'agit du
Grand Théorème de Fermat. Pourquoi
théorème alors que cela n'était
qu'une conjecture et de quoi s'agissait-il ?
Pierre de Fermat était un magistrat toulousain du dix-septième
siècle et il pratiquait en amateur l'art des Mathématiques,
comme d'autres cultivent leur jardin. Mais cet amateurisme ne doit
pas masquer les contributions fondamentales qui lui sont dues en :
- arithmétique,
- probabilité,
- calcul infinitésimal dont il fut l'un des précurseurs,
- physique (principe éponyme),
- etc...
Il avait en sa possession une copie de l'Arithmetica
de Diophante. Cet ouvrage, écrit au troisième siècle de notre ère, contenait de
nombreux problèmes d'arithmétique et en particulier la recherche des solutions entières de certaines équations
(dites diophantiennes). Par exemple,
existe-t-il des triangles rectangles à côtés entiers. Soient
{X,Y,Z} respectivement les deux côtés de l'angle droit et l'hypoténuse
d'un tel triangle ; le théorème de Pythagore s'écrit :
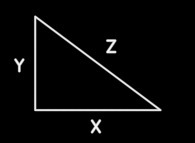
2 2 2
X + Y = Z
le problème est donc de trouver 3 nombres entiers {X,Y,Z}
satisfaisant à l'équation précédente. Il est facile de démontrer qu'elle admet une infinité
de solutions dont la plus fameuse est certainement le triplet {3,4,5} :
2 2 2
3 + 4 = 5
Pierre de Fermat eut l'idée de généraliser le problème
et de s'intéresser donc à l'équation :
n n n
X + Y = Z
{X,Y,Z,n} ∈ N
(n étant aussi un nombre entier).
Il pensa avoir découvert une "merveilleuse solution trop
longue pour figurer dans la marge de l'ouvrage", mais dont
aucune trace ne fut trouvée par la suite et qui démontrait que cette équation
n'avait pas de solution pour n strictement supérieur a 2
(sans oublier qu'il en est de même dans le cas trivial où n est nul...).
Il parait aujourd'hui évident que Pierre de Fermat s'est rapidement
rendu compte que sa démonstration présentait un défaut, mais
malgré tout, cette conjecture resta appelée
le Grand Théorème de Fermat.
Nombreux furent ceux qui s'y attaquèrent et parfois certaines
erreurs furent commises. De nombreux
cas particuliers (pour certaines valeurs de n)
furent vaincus et il fallu attendre 1994
pour que Andrew Wiles (aujourd'hui Sir Andrew Wiles) fournissent la solution générale.
Alors, à quoi sert le Grand Théorème de Fermat ?
Il semblerait qu'a priori il ne serve
à rien. Mais est-ce bien vrai ? En réalité sa démonstration
a d'une part révélée des liens "inimaginables" entre différentes branches
des Mathématiques :
et qui sait si demain il ne se révèlera pas être la
clef d'un autre grand mystère ?
D'autre part, certains "outils" qui furent
utiles à sa démonstration ont déjà trouvé des applications concrètes. En
particulier les courbes elliptiques semblent offrir
de nouvelles possibilités de cryptage de l'information
(aujourd'hui la plupart des méthodes utilisées de par
le monde sur les réseaux de télécommunications
pour préserver l'intégrité du contenu des messages,
empécher leur lecture et permettre
leur non répudiation, reposent sur la difficulté -non démontrée, mais conjecturée-
de factoriser, avec un ordinateur classique -c'est-à-dire non quantique-,
les grands nombres entiers -de plusieurs centaines de chiffres-).
Ainsi, le mathématicien dit "pur" ne se soucie
pas a priori des applications de ses
recherches, mais l'artiste ou le joueur d'échec
ne procèdent-ils pas de même ? Les Mathématiques Pures
constituent certainement la recherche tout à la fois la plus abstraite
et la plus proche de nos structures cérébrales les plus fondamentales ;
elles sont à la fois Jeu Intellectuel, Art et Science,
Langage, Mémoire et Pensée,
mais aussi le terreau sur lequel se développe notre Science.
4-Les Mathématiques Appliquées :
Les Mathématiques Appliquées, comme leur nom l'indique,
sont toujours issues de problèmes concrets posés par la recherche
fondamentale mais aussi, de plus en plus, par
la recherche industrielle. Par la suite, nous nous
limiterons à la recherche fondamentale et plus particulièrement
à ce qui se fait en Physique.
4.1-La Recherche en Physique :
Pour bien comprendre de quoi il s'agit,
il est important de rappeler en quoi consiste
l'activite du physicien.
4.1.1-L'Observation et la Mesure :
Depuis l'aube des temps, l'homme observe l'Univers,
note les régularités, les symétries, les
constances auquel son sens de la vision (certainement donc
à l'origine de la curiosité scientifique) lui donnent accès.
Que serait notre science si nos sens ne nous livraient
que notre environnement proche (les sons, par
exemple, n'ont qu'une très faible portée,
alors que les rayonnements électromagnétiques, et
la lumière en particulier, nous donnent
"des nouvelles de l'infini").
L'acte fondamental du physicien est la mesure (mesure de
coordonnées, de vitesses, de températures,
de pressions,...). Les valeurs ainsi engrangées
doivent être ensuite synthétisées et décrites à l'aide
d'un langage permettant la communication la plus
objective possible (dans le sens où les langues naturelles, quant à elles,
sont fortement ambigües et subjectives), dans le but ultime de disposer d'une
description unitaire de la Réalité.
4.1.2-La Modélisation :
Le langage utile à cette tache (utopique ?) est celui
des Mathématiques, qui se sont révélées, au cours des siècles,
être dans cette tâche d'une redoutable efficacité ; cela signifie-t-il pour autant
que nous ayons perce le secret ultime du Grand Horloger ?
Certains le croient, mais pour moi, cette
étonnante adéquation des Mathématiques à la description
de l'Univers ne serait lié d'une part qu'à l'absence de chaos absolu
(dans le cas contraire, nous ne serions pas la
pour discerter sur ce sujet...) ; par analogie avec la
compression d'informations (par exemple, celle qui
a donné naissance aux codages d'images de type JPEG),
l'existence de régularités doit nécessairement impliquer
la possibilité de décrire le tout d'une façon beaucoup plus économique
(et surtout plus utile...)
que celle qui consisterait à realiser un impossible inventaire exhaustif.
D'autre part, partant des postulats ("personnels") suivants :
- notre imagination est conditionnée et informée par nos perceptions,
- les Mathématiques sont le pur fruit de cette même imagination
(elles n'existent pas en dehors de nous, tout comme
les langues naturelles, la morale ou encore l'art...),
alors, nos Mathématiques ne "percoivent" que ce que nous percevons ; étant évident,
pour moi, que nos sens sont "infiniment" limités, nous ne décrivons
ainsi qu'une infime partie de la Réalité, le reste nous échappant à jamais
(rappelons à ce propos que c'est principalement grâce au sens de la vision
-et donc au rayonnement électromagnétique-
que nous prenons connaissance de notre "environnement" ; comment percevrions-nous ce dernier
si nous n'avions que le sens de l'audition, dont la portée est très limitée ?
Les étoiles, par exemple, existeraient-elles pour nous ?
Alors, quels sens supplémentaires nous faudraient-ils pour appréhender
l'infinie richesse de la Réalité ?)...
Dans cette optique, nos Mathématiques ne seraient alors
qu'un langage, parmi beaucoup d'autres
(qui, sans doute, nous resteront inaccessibles à jamais,
parce que liés à des formes d'intelligence qui nous sont
complètement étrangères, voire "orthogonales"...), de description
d'un infime sous-ensemble de la Réalité.
Une autre explication peut être avancée : l'intégralité de la réalité que nous percevons
et dont nous sommes faits pourrait n'être que le résultat d'une gigantesque simulation
effectuée à une échelle supérieure à la nôtre (nous commençons nous-mêmes, de
façon plus modeste, à en réaliser de telles). Nous, alors simples
intelligences artificielles, serions tout simplement
en train, depuis des siècles, d'accéder aux programmes
correspondants et d'en déchiffrer le langage (les Mathématiques...).
Certains qualifieront d'extravagante cette explication, d'autres la renverront
à la science-fiction. Mais en fait, rien ne permet d'en démontrer la fausseté,
si ce n'est en invoquant, à juste titre, le principe d'Occam.
4.1.3-La Prédiction :
Ainsi, nos Mathématiques constituent
le Langage et la Mémoire
de la Sience et de la physique en particulier. Mais elles
sont aussi une Pensée ce qu'illustre parfaitement la remarque
faite par Heinrich Hertz au dix-neuvième siècle :
on ne peut échapper au sentiment que ces formules mathématiques
ont une existence qui leur est propre, qu'elles sont plus savantes que
ceux qui les ont découvertes, et que nous pouvons en extraire plus de science
qu'il n'en a ete mis à l'origine. Ainsi, la "manipulation"
des équations contenus dans les
modèles mathématiques des systèmes étudiés
pourra permettre la découverte de phénomènes nouveaux
que l'expérience devra ensuite confirmer ou infirmer
(toute théorie scientifique se devant d'être réfutable).
Notons au passage une différence fondamentale entre le mathématicien (l'inventeur)
et le physicien (l'explorateur) :
le premier aboutit, par ses démonstrations, à des certitudes absolues
(par exemple,
le théorème de Pythagore évoqué précédemment, affirme que tous les triangles
rectangles, sans exception, possèdent une certaine propriété, par
ailleurs invérifiable : en effet, les triangles rectangles possibles sont en
nombre infini et la précision de nos mesures est évidemment limitée...) ; quant au
second, il évolue constamment dans le provisoire et dans la crainte (ou l'espoir ?)
permanente d'un phénomène nouveau qui viendra remettre en cause tout l'édifice théorique
qu'il a patiemment construit.
Donnons quelques exemples historiques et marquants de tout cela :
- En 1846, Urbain Le Verrier découvre, à partir
des équations de Newton,
la planète Neptune
(permettant ainsi d'expliquer les différences entre les prédictions
de la mécanique classique et les mesures toujours plus précises
de l'époque, sans renoncer au cadre théorique en vigueur).
- En 1915, Albert Einstein, utilisant la théorie
de la Relativité Générale qu'il vient de concevoir, prévoit la déviation des
rayons lumineux par la matière et c'est en 1919, au
cours d'une eclipse restée fameuse, que Sir Arthur
Stanley Eddington vérifiait, par la mesure, les
prédictions ainsi faites. Plus tard, d'autres physiciens
annonceront l'existence quasi-probable des trous noirs
ainsi qu'une origine possible pour l'Univers
(le Big Bang).
- En 1930, Paul Dirac annonce
l'existence de l'anti-électron
grâce à la Mécanique Quantique. D'autres
prédictions de cette dernière, beaucoup plus
choquantes pour l'intuition,
verront aussi le jour ; par exemple,
la non localité
testée expérimentalement par Alain Aspect grâce aux inégalités de Bell.
[pour avoir plus d'informations sur ce sujet]
4.1.4-Le Mathématicien et le Physicien :
Il est loin le temps où les grands esprits étaient à la fois Mathématiciens
et Physiciens, comme le fut, par exemple, Isaac Newton.
Aujourd'hui, sauf exception (Edward Witten, l'un des grands noms de la
théorie des super-cordes, a reçu la Médaille Fields), il s'agit de
deux mondes séparés. Le physicien pose des problèmes, émet des conjectures
(par exemple celle de la dimension fractale d'un front de diffusion),
alors que le mathématicien tentera de résoudre formellement ces problèmes (Wendelin Werner
a recu la Medaille Fields en 2006, en particulier, pour la résolution du problème
évoqué précédemment). Il convient
de remarquer que parfois, tel Monsieur Jourdain qui disait de la prose sans
qu'il en sut rien, le Mathématicien pur fait parfois de
de la Physique sans le savoir ; ce fut ainsi le cas d'Evariste Galois lors de ses
travaux sur la résolution par radicaux des équations algébriques et qui, a cette occasion,
a défini la notion de groupe, aujourd'hui absolument fondamentale dans
tous les domaines de la physique (et en Mécanique Quantique en particulier...).
4.2-Quelques exemples :
4.3-Les Limites :
Même si les succès de cette approche mathématique de la Connaissance
sont considérables, il est essentiel de rester humble et
d'adopter une attitude "copernicienne" (nous ne sommes pas le centre
de l'Univers et notre vue des "choses" est partielle et limitée,
nos Mathématiques ne sont pas Le Langage Universel,...).
D'ailleurs nous savons déjà que nos outils possèdent des limites fondamentales,
parmi lesquelles nous pouvons citer :
- L'incomplétude des Mathématiques (suite aux travaux de Gödel),
- La difficulté, voire l'impossibilité de construire
des représentations "naïves" (textuelles en langues naturelles
et surtout visuelles) des objets étudiés.
En particulier, les images du type de celles qui
furent présentées précédemment contraignent, pour les
réaliser, à répondre à des questions qui bien souvent
n'ont pas de sens. Ainsi, par exemple,
quelle est la forme d'un nucléon ?
ou encore
quelle est la couleur d'un champ scalaire -de pression, de température,...- ?
- L'impossibilité, en toute généralité, de manipuler exactement les Nombres Réels dans un Ordinateur (mais d'ailleurs, pourquoi semblent-ils indispensables à la physique ?).
Les deux dernières limites sont atteintes quotidiennement,
alors que la première pourrait se manifester, selon certains théoriciens,
en gravitation quantique.
5-Conclusion :
Plutôt que la Réalité Ultime, nos Mathématiques ne sont peut-être
qu'un reflet de nos structures cognitives les plus profondes
et progresser dans cette matière, c'est aller vers une meilleure connaissance de nous-mêmes.
Enfin, elles possèdent un rôle structurant fondamental
et constituent actuellement notre meilleur outil
pour approcher (asymptotiquement ?) cette réalité transcendante dont nous
sommes faits et dans laquelle nous évoluons.
Elles sont peut-être the final frontier,
là où peut se vivre
l'ultime aventure moderne
et peut-être sauveront-elles l'humanité des catastrophes annoncées...
Copyright © Jean-François COLONNA, 2000-2024.
Copyright © France Telecom R&D and CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2000-2024.