
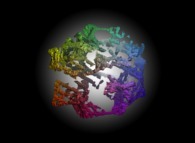
The intersection of the Menger Sponge -iteration 5- and of a quadridimensional Calabi-Yau manifold -tridimensional representation- [L'intersection d'une éponge de Menger -itération 5- et d'une variété quadridimensionnelle de Calabi-Yau -représentation tridimensionnelle-].
See the Calabi-Yau manifold:

See the Menger sponge:

See some related pictures (possibly including this one):





Definition of the "standard" Menger sponge (related to the Cantor triadic set): A cube is cut into 3x3x3=27 identical smaller cubes.
Then the 7 central subcubes
(6 for each face and 1 at the center of the cube) are removed.
At last this process is iterated recursively with the 27-7=20 remaining subcubes.
The fractal dimension of the Menger sponge is equal to:
log(20)
--------- = 2.726833027860842...
log(3)
The "standard" Menger sponge can be defined by means of subdivision rules.
Here is the way how each of the 27 cubes of the "standard" Menger sponge at a given level is subdivided:
"standard" Menger sponge
_____________________
/ \
TTT TFT TTT
TFT FFF TFT
TTT TFT TTT
\_/
Sierpinski carpet
or again:
TTT TFT TTT TFT FFF TFT TTT TFT TTT
where 'T' ('True') and 'F' ('False') means respectively "subdivide the current cube" and "do not subdivide and destroy the current cube".
The rules are repeated at each level, but they can be changed periodically and for example:
TTT TFT TTT TFT FFF TFT TTT TFT TTT FFF FTF FFF FTF TTT FTF FFF FTF FFF
\___________________________________/ \___________________________________/
"standard" Menger sponge complement
alternates the "standard" Menger sponge and its complement.
Obviously many other rules do exist as shown below...
Beside 'F' and 'T' some other possibilities exist: 'R' that means "subdivide the current cube" or "do not subdivide and destroy the current cube" Randomly
with a given threshold between 0 and 1 (0.5 being the default value)
and 'S' that means "Stop subdividing".
Obviously 'F', 'T', 'R' and 'S' can be mixed at will...
Moreover an amazing cross-section can be made using the plane:
2X - 2Y + 2Z - 1 = 0
the origin of the coordinates being at the center of the main cube
and the axis being parallel to its sides.
This process can be generalized in many different ways and for example:
3 3 3
2X - 2Y + 2Z - 1 = 0
(the curved one) or again:
1 2 1 2 1 2 2
(X - ---) + (Y - ---) + (Z - ---) = R
2 2 2
(the spherical one).
The "standard" Menger sponge:
See some related pictures (possibly including this one):










 ==>
==> 







 ==>
==> 







 >>>
>>> 








 ==>
==> 




 ==>
==> 














 ==>
==> 




 ==>
==> 




 ==>
==> 




 ==>
==> 
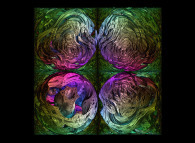
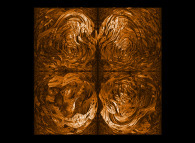
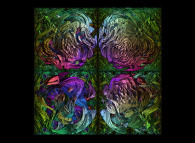
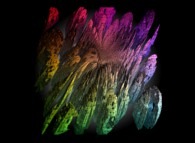
Some non linear transformations of the "standard" Menger sponge:
See some related pictures (possibly including this one):














 ==>
==> 









 ==>
==> 





The complement of the "standard" Menger sponge:
See some related pictures (possibly including this one):










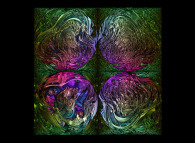
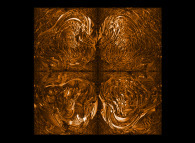
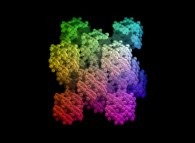
Some extended Menger sponges:
Two ways of extending the "standard" Menger sponge. On the one hand one can change the
used volume (from a cube to a sphere for example). On the other hand one can change the
rules of subdividing each cube as well as their numbers...
See some related pictures (possibly including this one):














 ==>
==> 




 ==>
==> 




 ==>
==> 





 >>>
>>> 












 ==>
==> 




 ==>
==> 




 ==>
==> 




 ==>
==> 




 ==>
==> 




 ==>
==> 




 ==>
==> 




 ==>
==> 




 ==>
==> 





 ==>
==> 




 ==>
==> 




 ==>
==> 
The fractal "standard" Menger sponge:
See some related pictures (possibly including this one):

















Definition of the Sierpinski carpet (related to the Cantor triadic set): A square is cut into 3x3=9 identical smaller squares.
Then the central subsquare -grey- is removed.
At last this process is iterated recursively with the 9-1=8 remaining subsquares.
The fractal dimension of the Sierpinski carpet is equal to:
log(8)
-------- = 1.892789260714372
log(3)
See the first objects of this family (including this one):

















(CMAP28 WWW site: this page was created on 10/22/2017 and last updated on 07/07/2024 12:14:15 -CEST-)
[See the generator of this picture [Voir le générateur de cette image]]
[See all related pictures (including this one) [Voir toutes les images associées (incluant celle-ci)]]
[Please visit the related ArtAndScience picture gallery [Visitez la galerie d'images ArtAndScience associée]]
[Please visit the related ArtisticCreation picture gallery [Visitez la galerie d'images ArtisticCreation associée]]
[Go back to AVirtualMachineForExploringSpaceTimeAndBeyond [Retour à AVirtualMachineForExploringSpaceTimeAndBeyond]]
[The Y2K Bug [Le bug de l'an 2000]]
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[Mail [Courrier]]
[About Pictures and Animations [A Propos des Images et des Animations]]
Copyright © Jean-François COLONNA, 2017-2024.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2017-2024.

















 ==>
==> 









 ==>
==> 









 ==>
==> 
 ==>
==> 


 ==>
==> 
 ==>
==> 
 ==>
==> 






 ==>
==> 

 ==>
==> 





















 ==>
==> 




 ==>
==> 




 ==>
==> 
















 ==>
==> 




 ==>
==> 




 ==>
==> 




 ==>
==> 




 ==>
==> 




 ==>
==> 




 ==>
==> 




 ==>
==> 




 ==>
==> 





 ==>
==> 




 ==>
==> 




 ==>
==> 
























