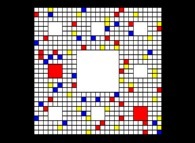
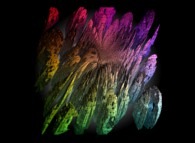
A half-random extended Menger Sponge -iteration 4- [Une éponge de Menger généralisée à moitié aléatoire -itération 4-].

A half-random extended Menger Sponge -iteration 4- [Une éponge de Menger généralisée à moitié aléatoire -itération 4-].





(SubdivisionRules=TTR TRR RRR TFT FFR TRR TTT TFT TTR)
log(20)
--------- = 2.726833027860842...
log(3)
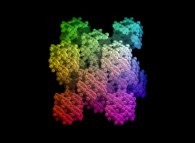
The "standard" Menger sponge can be defined by means of subdivision rules.
Here is the way how each of the 27 cubes of the "standard" Menger sponge at a given level is subdivided:
"standard" Menger sponge
_____________________
/ \
TTT TFT TTT
TFT FFF TFT
TTT TFT TTT
\_/
Sierpinski carpet
or again:
TTT TFT TTT TFT FFF TFT TTT TFT TTTwhere 'T' ('True') and 'F' ('False') means respectively "subdivide the current cube" and "do not subdivide and destroy the current cube". The rules are repeated at each level, but they can be changed periodically and for example:
TTT TFT TTT TFT FFF TFT TTT TFT TTT FFF FTF FFF FTF TTT FTF FFF FTF FFF
\___________________________________/ \___________________________________/
"standard" Menger sponge complement
alternates the "standard" Menger sponge and its complement.
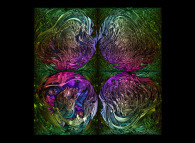
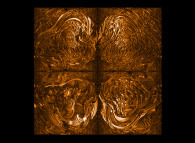
Obviously many other rules do exist as shown below...
2X - 2Y + 2Z - 1 = 0the origin of the coordinates being at the center of the main cube and the axis being parallel to its sides.
3 3 3
2X - 2Y + 2Z - 1 = 0
(the curved one) or again:
1 2 1 2 1 2 2
(X - ---) + (Y - ---) + (Z - ---) = R
2 2 2
(the spherical one).










 ==>
==> 







 ==>
==> 







 >>>
>>> 








 ==>
==> 




 ==>
==> 














 ==>
==> 




 ==>
==> 




 ==>
==> 




 ==>
==> 














 ==>
==> 









 ==>
==> 





























 ==>
==> 




 ==>
==> 




 ==>
==> 





 >>>
>>> 












 ==>
==> 




 ==>
==> 




 ==>
==> 




 ==>
==> 




 ==>
==> 




 ==>
==> 




 ==>
==> 




 ==>
==> 




 ==>
==> 





 ==>
==> 




 ==>
==> 




 ==>
==> 

















log(8)
-------- = 1.892789260714372
log(3)