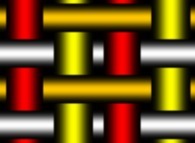
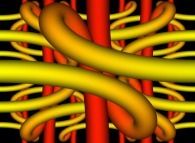
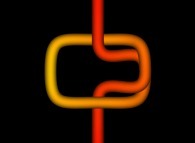
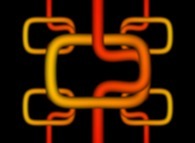
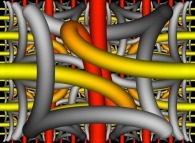
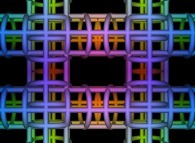
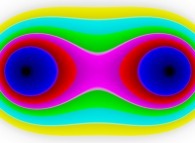
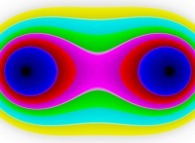
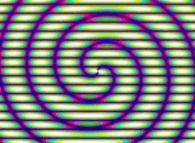
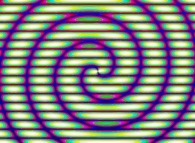
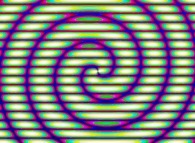
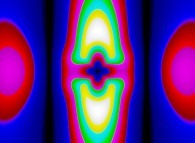
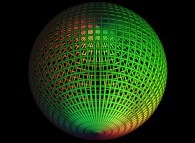
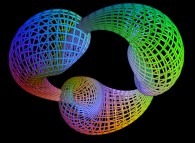
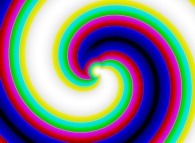
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= )
)
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= )
)
-
(PR= ) = (PX=
) = (PX=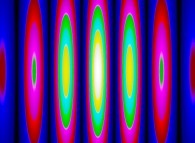 ,PY=
,PY= ,PZ=
,PZ=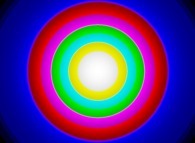 )(PA=
)(PA= )
)
-
(PR= ) = (PX=
) = (PX=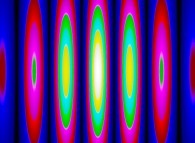 ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= )
)
-
(PR= ) = (PX=
) = (PX=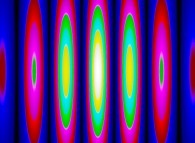 ,PY=
,PY= ,PZ=
,PZ=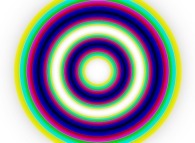 )(PA=
)(PA= )
)
-
(PR= ) = (PX=
) = (PX=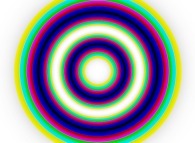 ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= )
)
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= )
)
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= )
)
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= )
)
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= )
)
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA=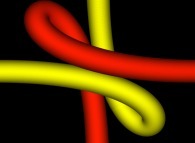 )
)
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= )
)
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= )
)
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= )
)
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= )
)
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= )
)
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= )
)
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= )
)
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= )
)
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= )
)
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= )
)
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= )
)
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= )
)
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= )
)
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= )
)
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= )
)
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= )
)
-
(PR= ) =TapestryEffect((PX=
) =TapestryEffect((PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA=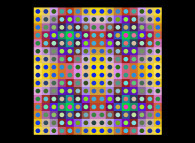 ))
))
-
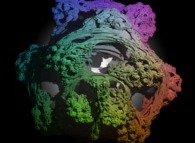
(PR= ) =MountainEffect(TapestryEffect((PX=
) =MountainEffect(TapestryEffect((PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA=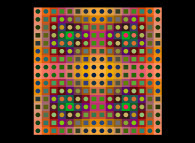 )))
)))
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= ) with a double mirror effect.
) with a double mirror effect.
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=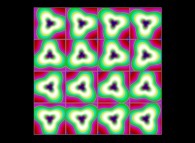 ,PZ=
,PZ=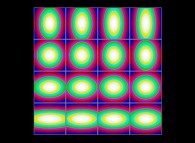 )(PA=
)(PA= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=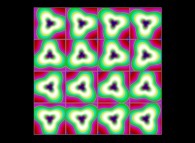 ,PZ=
,PZ=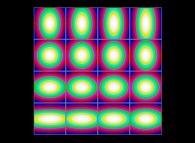 )(PA=
)(PA= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=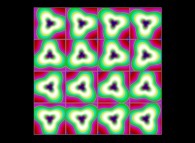 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=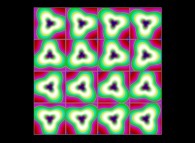 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=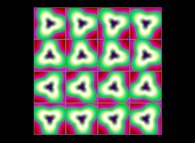 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=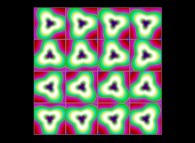 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=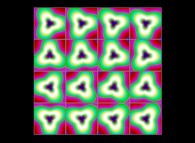 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=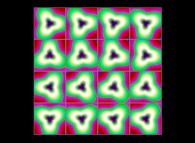 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=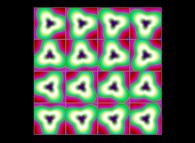 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=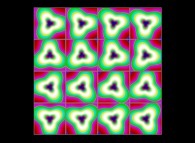 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=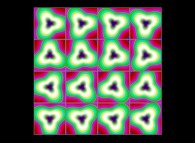 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=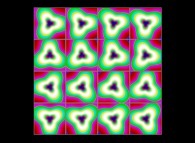 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=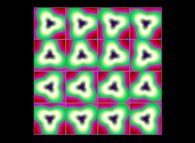 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=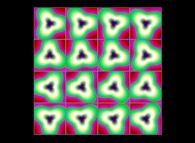 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=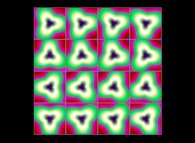 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=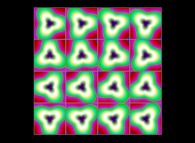 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=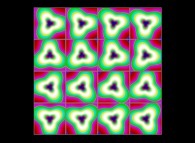 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=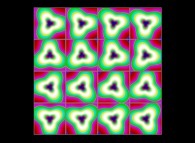 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=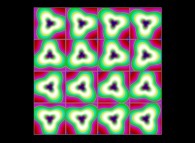 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=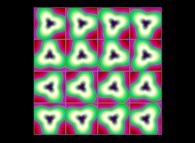 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX=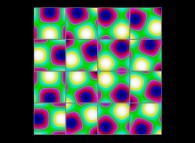 ,PY=
,PY=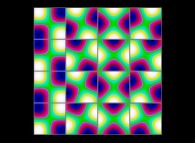 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ=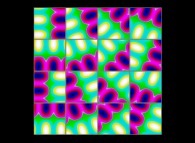 )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=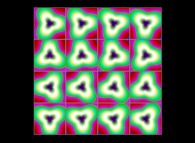 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=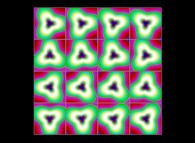 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=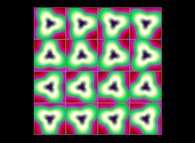 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=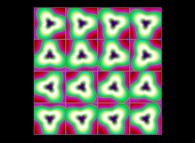 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=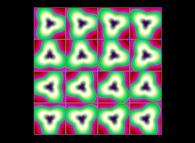 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=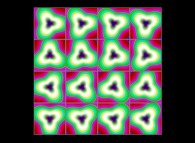 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=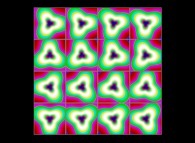 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=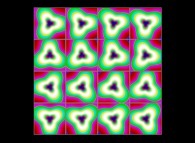 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX=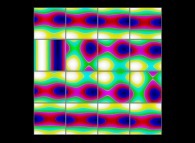 ,PY=
,PY=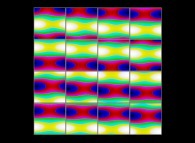 ,PZ=
,PZ=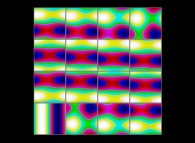 )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX=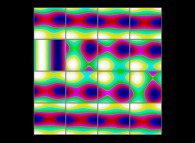 ,PY=
,PY= ,PZ=
,PZ=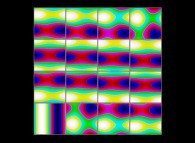 )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX=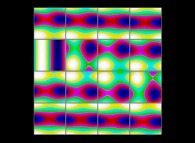 ,PY=
,PY=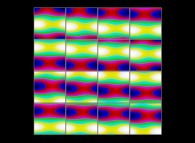 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX=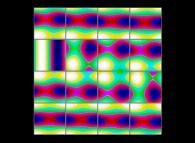 ,PY=
,PY=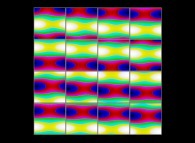 ,PZ=
,PZ=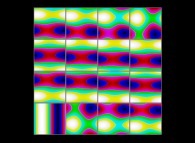 )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=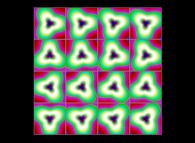 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=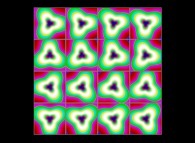 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=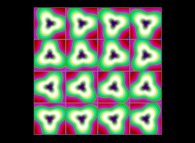 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=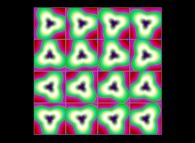 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=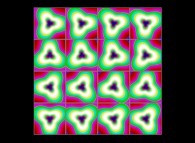 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=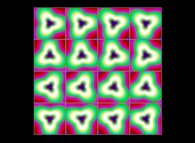 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=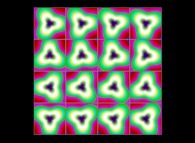 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=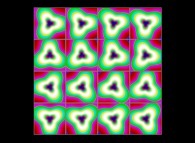 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=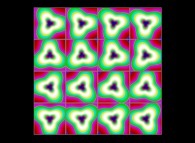 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=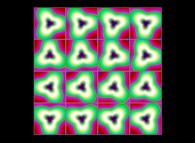 ,PZ=
,PZ= )(PA=
)(PA=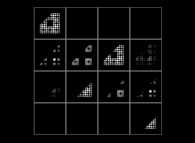 =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=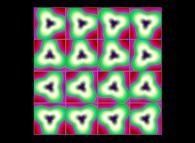 ,PZ=
,PZ= )(PA=
)(PA=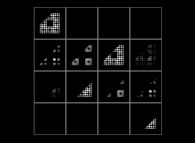 =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=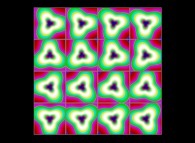 ,PZ=
,PZ= )(PA=
)(PA=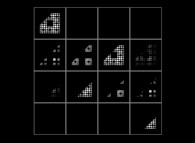 =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=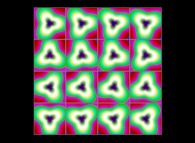 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=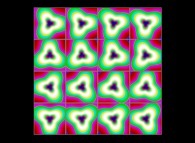 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=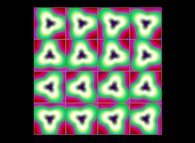 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=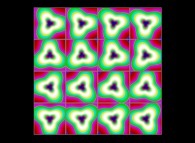 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=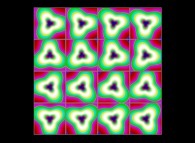 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=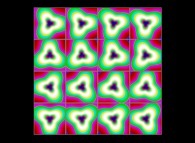 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=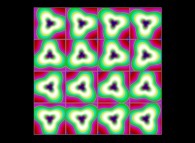 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=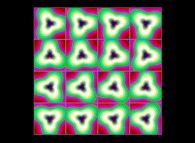 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=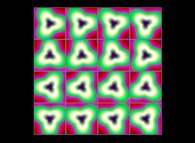 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=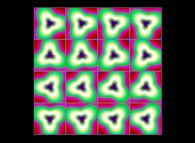 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=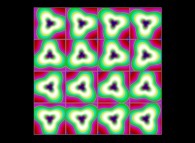 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=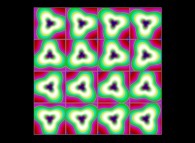 ,PZ=
,PZ= )(PA=
)(PA=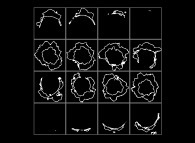 =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=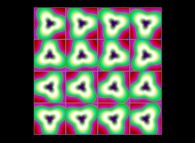 ,PZ=
,PZ= )(PA=
)(PA=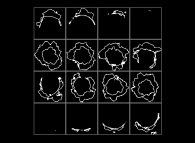 =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=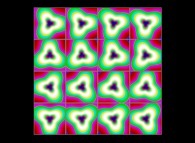 ,PZ=
,PZ= )(PA=
)(PA=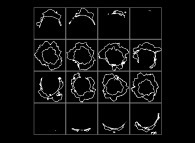 =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=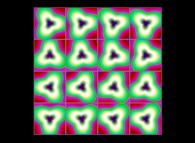 ,PZ=
,PZ= )(PA=
)(PA=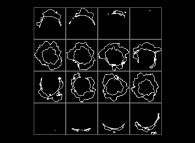 =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=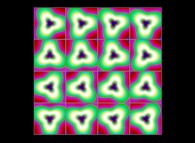 ,PZ=
,PZ= )(PA=
)(PA=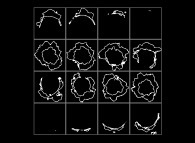 =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=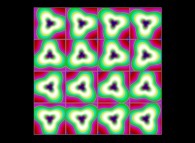 ,PZ=
,PZ= )(PA=
)(PA=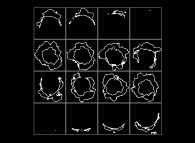 =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=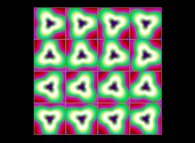 ,PZ=
,PZ= )(PA=
)(PA=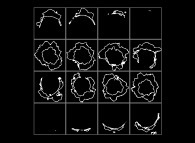 =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY=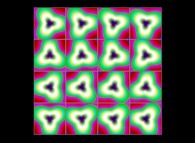 ,PZ=
,PZ= )(PA=
)(PA=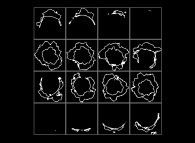 =
= ).
).
-
(PR= ) = (PX=
) = (PX=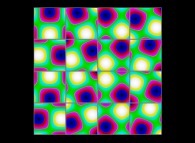 ,PY=
,PY=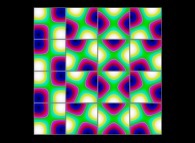 ,PZ=
,PZ= )(PA=
)(PA= =
= ).
).
-
(PR= ) = (PX=
) = (PX= ,PY=
,PY= ,PZ=
,PZ=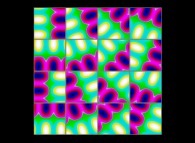 )(PA=
)(PA= =
= ).
).