Are Floating Point Computations Reliable?
or again
Is a Computer a Perfect Computing Machine?
CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France
france telecom, France Telecom R&D
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[Please, visit A Virtual Machine for Exploring Space-Time and Beyond, the place where you can find more than 10.000 pictures and animations between Art and Science]
(CMAP28 WWW site: this page was created on 03/22/2004 and last updated on 03/19/2025 13:32:35 -CET-)
[en français/in french]
Keywords: Floating Point Numbers, Nombres Flottants, Rounding-off Errors, Erreurs d'arrondi.
A computer is a finite machine (its memory has a given limited capacity)
and the data (in order to be manipulated) must be quantified and sampled.
These two characteristics can be at the origin of numerous problems...
As an example of the consequence of the finite nature of a computer,
let's study the following iteration:
S = 0
0
S = S + 1
n n-1
What is the current value of S(n)? Obviously, the
"mathematical" answer is:
S = n
n
Unfortunately, the "numerical" answer can be very different,
as exhibited with the following program:
#define N "an arbitrary integer positive value..."
main()
{
int n;
float sigma=0;
for (n=1 ; n <= N ; n++)
{
sigma = sigma + 1.0;
}
printf("\n computed sum = %f",sigma);
}
As soon as N >16777215, the answer is always 16777216 when the value N
is expected.
Another consequence is the impossibility to manipulate the Real numbers
with a computer. In this area, they do not exist and are roughly
approximated using the so-called floating point numbers.
Thus, very simple decimal numbers (for example
4095.1 et 4096.1 that will be useful later)
cannot be precisely defined.
Moreover, during arithmetical operations,
rounding-off errors are committed; these errors imply
the loss of the property of associativity for the addition and the multiplication.
Using 32-bit floating point numbers
(in order to simplify the hexa-decimal printing
-see the same experiment using 64 bit double precision-), the following progam
(where the function 'MUL' is used to specify the chronological order
of the operations):
float MUL(x,y)
float x,y;
{
return(x*y);
}
main()
{
float A=3.1,B=2.3,C=1.5;
float X,Y;
X=MUL(MUL(A,B),C);
Y=MUL(A,MUL(B,C));
printf("\n (%f x %f) x %f = %f\n",A,B,C,X);
printf("\n %f x (%f x %f) = %f\n",A,B,C,Y);
}
produces the following results:
(3.10 * 2.30) * 1.50 = 10.695000 = 0x412B1EB8
#### #
and:
3.10 * (2.30 * 1.50) = 10.694999 = 0x412B1EB7
#### #
that are two slightly different values.
Moreovoer, this experiment can be done with any programming
language (for example java where the order
in which the arithmetical operations are performed is known,
but is that true?).
This last experiment could be tried with the following program:
main()
{
float A=3.1,B=2.3,C=1.5;
float X,Y;
X=(A*B)*C;
Y=A*(B*C);
printf("\n (%f x %f) x %f = %f",A,B,C,X);
printf("\n %f x (%f x %f) = %f",A,B,C,Y);
}
When it does not exhibit the preceding phenomenon,
at least two explanations can be found:
- the compiler replaces 32-bit computations
with 64-bit ones,
- the compiler translates in the same way the two
expressions (AxB)xC and Ax(BxC).
Then, the best thing to do is to use the program
defining the 'MUL' function...
The property of associativity for addition is lost too.
Using 32-bit floating point numbers
(in order to simplify the hexa-decimal printing
-see the same experiment us
ing 64 bit double precision-), the following progam
(where the function 'ADD' is used to specify the chronological order
of the operations):
float ADD(x,y)
float x,y;
{
return(x+y);
}
main()
{
float A=1.1,B=3.3,C=5.5;
float X,Y;
X=ADD(ADD(A,B),C);
Y=ADD(A,ADD(B,C));
printf("\n (%f x %f) x %f = %f\n",A,B,C,X);
printf("\n %f x (%f x %f) = %f\n",A,B,C,Y);
}
produces:
(1.10 + 3.30) + 5.50 = 9.900000 = 0x411E6666
# #
that is slightly different from:
1.10 + (3.30 + 5.50) = 9.900001 = 0x411E6667
# #
[Obviously a similar anomaly can be seen with the distributivity of the multiplication over the addition]
This "anomaly" is very helpfull to recall us that a computer
is not able to perform, except for some particular cases
(the one of small integer numbers, for example),
exact computations!
When studying non linear phenomena, the consequences
can be devastating. For example, the computation
of the so-called Verhulst Dynamics iteration:
2
X = (R+1)X - RX
n n-1 n-1
that means the following successive computations:
X
0
|
---------------
| |
\|/ \|/
' '
2
X = (R+1)X - RX
1 0 0
|
---------------
| |
\|/ \|/
' '
2
X = (R+1)X - RX
2 1 1
|
---------------
| |
\|/ \|/
' '
2
X = (R+1)X - RX
3 2 2
|
---------------
| |
\|/ \|/
' '
etc...
can be done with the following elementary program (that cannot be wrong...):
main()
{
double R=3.0;
double X=0.5;
int n;
for (n=0 ; n <= 80 ; n++)
{
if ((n%10) == 0)
{
printf("\n iteration(%04d) = %9.6f",n,X);
}
else
{
}
X = (R+1)*X - R*X*X;
}
}
produces the following results on a O200 Silicon Graphics computer
(R10000 processor under IRIX 6.5.5m with cc 7.2.1) depending on the
optimization options:
O200 Silicon Graphics (R10000, IRIX 6.5.5m, cc 7.2.1):
option '-O2' option '-O3'
X(00) = 0.500000 0.500000
X(10) = 0.384631 0.384631
X(20) = 0.418895 0.418895
X(30) = 0.046399 0.046399
X(40) = 0.320184 0.320192
X(50) = 0.063747 0.059988
X(60) = 0.271115 1.000531
X(70) = 1.328462 1.329692
X(80) = 0.817163 0.021952
It is easy to compute the extrema of each intermediate results
and to check that they are always compatible together; that means
that two values of very different magnitude never appear. By the
way this is another source of problems; for example,
using 64-bit numbers the following equality is true:
16 16
10 + 1 = 10
Regarding the significance of the syntax used,
here is an experiment (with R = 3.0) using Java
(a language known for write once, run everywhere...)
where all variables are double ones.
The preceding iteration is computed on two different computers
using five equivalent formulas:
O200 Silicon Graphics (processeur R10000, IRIX 6.5.5m, Java):
(R+1)X-R(XX) (R+1)X-(RX)X ((R+1)-(RX))X RX+(1-(RX))X X+R(X-(XX))
X(0000) = 0.5 0.5 0.5 0.5 0.5
X(0500) = 1.288736212247168 0.007057813075738616 1.2767485100695732 1.246534177059494 0.03910723014701789
X(1000) = 1.3327294162589722 0.916560711983132 1.207710752523091 0.27770146115891703 0.26663342726567785
X(1500) = 1.1448646685382955 0.4481000759915065 0.3102077001456977 0.015374092695375374 0.9841637252962943
X(2000) = 1.0548628914440754 0.896126931497168 0.6851138190159249 0.009229885271816535 0.3860923315999224
X(2500) = 1.292802584458599 0.06063433547953646 1.174118726001978 0.6922411856638806 0.020878761210912034
X(3000) = 1.0497821908090537 0.0219606878364607 1.3287403237319588 0.11354602472378028 0.13270749449424302
X(3500) = 0.8115039383609847 1.3213031319440816 0.6545151597367076 0.5760786099237328 1.324039473116061
X(4000) = 0.04922223042798102 1.3203298564077224 0.09243804931690679 0.9496284087750142 1.316597313359563
X(4500) = 0.4745896653599724 0.32865616721789603 0.018965010461877246 0.25384661313701296 0.18512853535354462
PC (processeur Pentium II, LINUX Mandrake 7.0, Java):
(R+1)X-R(XX) (R+1)X-(RX)X ((R+1)-(RX))X RX+(1-(RX))X X+R(X-(XX))
X(0000) = 0.5 0.5 0.5 0.5 0.5
X(0500) = 1.2887362122471679 0.00705781307573862 1.2767485100695732 1.2465341770675666 0.03910723014701789
X(1000) = 1.3327294162589722 0.91656071198313205 1.207710752523091 0.6676224369769922 0.26663342726567785
X(1500) = 1.1448646685382955 0.44810007599150647 0.31020770014569771 0.41049165176544455 0.98416372529629426
X(2000) = 1.0548628914440754 0.89612693149716804 0.68511381901592494 1.0026346845706315 0.3860923315999224
X(2500) = 1.3328681064703032 0.06063433547953646 1.1741187260019781 0.0154001182074282 0.02087876121091203
X(3000) = 1.2956769824648844 0.0219606878364607 1.3287403237319588 0.50504896336548377 0.13270749449424302
X(3500) = 0.19193027175727995 0.37986077053509781 0.6545151597367076 0.38299434265835819 1.324039473116061
X(4000) = 1.2491385720940165 0.96017143401896088 0.09243804931690679 0.6565274346305322 1.316597313359563
X(4500) = 0.00644889182443986 1.3185465795235045 0.01896501046187725 0.94966313327336349 0.18512853535354462
It is noteworhty that the two computers do not give the same results...
It is mandatory to give without ambiguity the name of the operating
system and of the compiler, as well as their releases,
when reporting that kind of experiment...
By the way this very small program cannot be wrong and does not
use any numerical methods of approximations. All these wrong results shows that
this program does not compute the values of the Verhulst Dynamics
iteration. So, what is this program computing?
To increase the precision of the computation is not very useful
as exhibited whit the following experiment using bc
("arbitrary-precision arithmetic language"). The following array
displays the maximum number of iterations n giving the exact integer
value of X(n) according to the precision (parameter scale):
scale = 010 020 030 040 050 060 070 080 090 100
n = 035 070 105 136 169 199 230 265 303 335
This improvement is too costly to be useful...
The preceding experiments were about non linear systems.
But what is about linear models? Let us study
the following program:
main()
{
double B=4095.1;
double A=B+1;
double x=1;
int n;
printf("initialisation x = %.16f\n",x);
for (n=1 ; n <= 9 ; n++)
{
x = (A*x) - B;
printf("iteration %01d x = %+.16f\n",n,x);
}
}
The computed values (after a 'gcc' compilation without optimization on a Linux PC) are as follows:
initialisation x = +1.0000000000000000
iteration 1 x = +1.0000000000004547
iteration 2 x = +1.0000000018630999
iteration 3 x = +1.0000076314440776
iteration 4 x = +1.0312591580864137
iteration 5 x = +129.0406374377594148
iteration 6 x = +524468.2550088063580915
iteration 7 x = +2148270324.2415719032287598
iteration 8 x = +8799530071030.8046875000000000
iteration 9 x = +36043755123945184.0000000000000000
Initially:
x = 1
and the following relation holds:
A-B = 1 (mathematically speaking...)
(it is noteworthy that 'A' equals a power of 4 plus 0.1; when using
another decimal part, things are more complicated...)
then, the variable 'x' should be equal to its
initial value (1) all along the iterations.
Or it is not true...
By the way, this program gives the right answer (1) when substituting
double with float
(that means that, "by chance", A-B equals 1 exactly) or
again compiling with optimization!
Obviously this phenomenon is independent of the programming language used
(provided the corresponding compilers and/or interpreters reference floating point numbers...)
as can be seen with the C,
Fortran 95
or again Python
versions of this program without iterations (for the sake of simplicity).
Then, it is very important not to confuse
mathematical linearity and
numerical linearity; the preceding
example is non linear at the numerical level for there is one
multiplication using a constant value (in a computer memory,
the difference between a constant value and a variable one is very light...)!
By the way, these very simple decimal numbers
cannot be precisely defined:
B = 4095.1 = {0x40affe33,33333333}
A = B+1 = 4096.1 = {0x40b00019,9999999a}
A-B = 1.0000000000004547 = {0x3ff00000,00000800}
|
1.0 = {0x3ff00000,00000000}
the preceding values being obtained with a PC.
A similar phenomenon is in fact very common: see for
example 1/3 that is a finite sum of powers of 1/3
(0.1 using base 3) and
in the same time an infinite sum of powers of 1/10 (0.33333...).
The consequences
are numerous; numerical results obtained with a computer
will depend on:
These problems will be encountered a priori
with models that are sensitive to the initial conditions
and even with linear models as seen earlier...
The simultaneous use of two or more precisions can be a source of problems too.
The so-called excess precision problem, known
from the 'gcc' specialists, can be encountered on Intel PCs.
For example, for two equal numbers 'A' and 'B', the two
following relations 'A = B' and 'A > B' can be true!
The "scenario" is as follows:
- 'A' and 'B' are two equal numbers stored in the 80-bit
floating point unit ('FPU').
At that time, it is possible to add them,
to multiple them,... and to compare them without ambiguity.
- Suppose that due to a lack of floating point resources,
the number A is moved to memory (and then in a 64-bit format)
and suppose that the optimizer "ignores" (as it is the case
unfortunately...) that move.
- Imagine that some instructions later,
'A' (now a 64-bit number) and 'B' (still a 80-bit number) have
to be compared; 'A' is moved from memory to a floating point register
and 16 (null) bits are added to it. A and B are no more equal!
On march 2004, this phenomenon can be seen with the following program:
double f(x)
double x;
{
return(1/x);
}
main()
{
double x1=f(3.0);
volatile double x2;
x2=x1;
if (x2 != x1)
{
printf("DIFFERENT\n");
}
}
This program, when compiled with 'gcc -O3 -fno-inline' on a Linux PC with
a x86 Intel processor, prints the "DIFFERENT" message!
Please note that on march 2018, this program works perfectly...
A universal solution (independent of the processor and of the compiler) to this problem
seems to test numbers by means of functions, thus moving them to the stack
using the 64-bit format. For example, the following test:
A > B
where 'A' and 'B' denote two 64 bit floating point numbers, will be written:
fIFGT(A,B)
the function 'fIFGT(...)' being defined as:
unsigned int fIFGT(x,y)
double x;
double y;
{
return(x > y);
}
and avoiding the function inlining process (option '-fno-inline' of 'gcc')...
Using functions in order to execute the elementary instructions
(addition, substraction, multiplication, division, tests,...)
of a program offers another advantage: it allows a
precise order for their execution,
when, as exhibited earlier, the results can depend
on this order.
For example, these two pictures
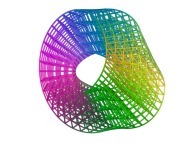 and
and 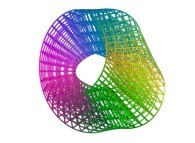 ,
computed using a non iterative process
on the same machine (a Linux PC) with and without imposing the order respectively,
look similar, when they are in fact
slightly different.
,
computed using a non iterative process
on the same machine (a Linux PC) with and without imposing the order respectively,
look similar, when they are in fact
slightly different.
At last, an error computation (in order to evaluate the quality
of a set of results) is in general of the same type that the computation
itself. Then the error computed will exhibit the same anomalies in this circonstances...
The N-body problem is a useful example of these problems.
So, why do we need real numbers to do physics?
Copyright © Jean-François COLONNA, 2004-2025.
Copyright © France Telecom R&D and CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2004-2025.
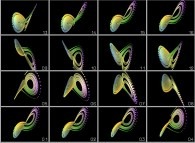
 and
and  ,
computed using a non iterative process
on the same machine (a Linux PC) with and without imposing the order respectively,
look similar, when they are in fact
slightly different.
,
computed using a non iterative process
on the same machine (a Linux PC) with and without imposing the order respectively,
look similar, when they are in fact
slightly different.