Les Nombres et la Lumière
CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[Real Numbers don't exist in Computers and Floating Point Computations aren't safe. [Les Nombres Réels n'existent pas dans les Ordinateurs et les Calculs Flottants ne sont pas sûrs.]]
[N'oubliez pas de visiter Une Machine Virtuelle à Explorer l'Espace-Temps et au-delà où vous trouverez plus de 10.000 images et animations à la frontière de l'Art et de la Science]
(Site WWW CMAP28 : cette page a été créée le 08/08/2009 et mise à jour le 17/10/2024 11:39:59 -CEST-)
Mots-Clefs :
A2M,
An 2000,
Bogue,
Bug,
Bugix,
Millenium Bug,
Year 2000 Problem,
Y2K,
Y2K Bug,
Anaglyphes,
Art et Science,
Autostéréogrammes,
Chaos Déterministe,
Création Artistique,
Entrelacs,
Erreurs d'arrondi,
Expérimentation Virtuelle,
Génie Logiciel,
Géométrie Fractale,
Infographie,
Mathématiques,
Mécanique Céleste,
Mécanique Quantique,
Physique,
Sensibilité aux Erreurs d'Arrondi,
Simulation Numérique,
Stéréogrammes,
Synthèse de Phénomènes Naturels,
Synthèse de Texture,
Visualisation Scientifique,
Voyage Virtuel dans l'Espace-Temps.
J'ai commencé ma carrière en 1970, pendant mon service militaire...
A cette époque les ordinateurs occupaient
des salles entières 
alors que leur capacité mémoire était de l'ordre
de quelques dizaines de milliers d'octets et les fréquences d'horloge de l'ordre
du méga-hertz ! L'entrée des instructions et des données se faisait à
l'aide de fragiles
cartes perforées 
,
alors que la sortie des résultats
utilisait des imprimantes alphanumériques 
bruyantes : point d'écran couleur
et encore moins de souris à cette époque ! Les programmes que l'on développait
sur ces machines était en général très dépendant des systèmes utilisés
: ici encore, point de Linux et de langages évolués...
Mes premières recherches concernèrent
l'Enseignement Assisté par Ordinateur.
Le T1600 
, l'ordinateur acquis
à cette occasionViRgUlE avait une mémoire de 32 Ko et initialement trois disques durs de 500 Ko
chacun ! Aucun logiciel n'était disponible sur cette machine, mis à
part un simple assembleur : tout était donc à faire. La première étape
fut donc de concevoir un système d'exploitation (CMS4) : malgré les très
sévères limitations, il fut conçu comme un réseau d'une centaine
de machines virtuelles responsables chacune d'un service élémentaire (gestion
d'un périphérique d'entrée-sortie, d'un fichier ou encore d'un utilisateur,...)
permettant une utilisation multi-tâches et multi-utilisateurs. La seconde étape
fut celle des applications, afin de permettre la description et la diffusion
des cours. Les terminaux-élève se composaient chacun d'un écran graphique
Tektronix alimenté en informations par l'ordinateur et d'un téléviseur couleur
recevant des séquences vidéos stockées sur un ensemble de magnétoscopes
télécommandés. Les cours étaient donc multi-médias et décrits dans
l'ordinateur sous la forme de graphes ordonnançant interactivement l'ordre d'apparition
des différents items. Afin de ne pas se limiter à des présentations textuelles,
un langage graphique tridimensionnel interprétatif (G3) fut conçu à cette
occasion : chose impensable aujourd'hui, son interpréteur, écrit
en assembleur, n'occupait qu'un seul kilo-octet et malgré cela,
comme le montrent les figures
1, 2 et 3,
il permettait déjà la conception de documents fort complexes.
Figure 01 :
Trois pages extraites d'un document décrivant le système d'exploitation CMS4 (1974).
Figure 02 :
Quelques structures paradoxales et autres (1974).
Figure 03 :
Hommage à Botticelli et à Bruegel l'Ancien (1974).
Rapidement se posa le problème de la conception des séquences
vidéos. Evidemment cet ordinateur (comme aucun autre à cette époque...)
n'était pas prévu pour cela, en particulier au niveau matériel.
Notant le parallèle qui pouvait être fait entre la structure d'un disque (fait
de pistes elles-mêmes découpées en un certain nombre de secteurs) et celle
d'une image (faite de lignes elles-mêmes composées de points), je décidai
de convertir l'un des coupleurs disque en un générateur vidéo. Cela pris
quelques jours et les premières images vidéos numériques sortirent de la
machine ; leur définition ferait sourire aujourd'hui : 256x256 points noir ou
blanc, mais ce furent des instants magiques. N'importe quelle zone de la
mémoire de l'ordinateur pouvait servir de frame buffer ; il était donc aussi
possible de visualiser un programme, voire le système d'exploitation lui-même, en cours de fonctionnement 
!
La réalisation d'images en couleurs était alors
plus délicate : il fallait procéder à la superposition de trois images noir
et blanc (coloriées à l'aide de filtres rouge, vert et bleu respectivement 
)
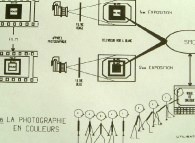sur une pellicule photographique 
. C'est ainsi que furent produites les images de
la figure 4. La sortie et l'entrée de sons numériques furent introduits peu
après et des outils d'associations sons-images réalisés 
pour exploiter cela.
Figure 04 :
Mes premières images en couleur (1974).
Les années qui suivirent virent
la réalisation de nombreux programmes, l'introduction de la vidéo animée
en couleurs, mais surtout un "glissement" important s'effectua,
conduisant mes recherches de l'Enseignement Assisté par Ordinateur à la Visualisation
Scientifique. En effet, d'une part mes activités avaient lieu au cœur
des laboratoires de recherche de l'Ecole Polytechnique et d'autre part arrivaient
sur le marché des ordinateurs toujours plus puissants (les super-ordinateurs 
).
Ils permettaient de traiter des problèmes toujours plus complexes ; mais calculant
plus rapidement, ils produisaient évidemment plus de résultats numériques.
Autant, il peut paraître raisonnable d'imprimer une dizaine, voire
une centaine, de valeurs numériques, autant cela est pure folie
s'il s'agit de plusieurs milliards de nombres ! L'idée naturelle fut donc de convertir
ces chiffres en images animées 
(parce que les modèles mathématiques de la
physique sont généralement dynamiques) et en couleur (afin de pouvoir véhiculer
le maximum d'informations), profitant de l'expérience acquise antérieurement.
Simultanément,
une "catastrophe" se produisit : tous les développements logiciels faits
jusqu'alors l'avait été en assembleur sur un système très spécifique.
La nécessité de renouveler les équipements posait donc un sérieux problème.
Je décidai de reprendre tout à zéro sur une base UNIX (aujourd'hui Linux)
et pour ne plus jamais me trouver confronter à de telles difficultés (même
sous UNIX/Linux où des problèmes de portabilité peuvent être rencontrés
!), je conçu un système virtuel et portable incluant en particulier
un langage de programmation et son traducteur en C. A cette occasion, le
Génie Logiciel (Software Engineering) devint un autre de mes sujets de recherche
[Plus d'informations à ce propos]
et la pérennité de tout "objet" informatique (programme, image,...)
l'une de mes préoccupations majeures.
Contrairement à une vue simpliste des
choses, la Visualisation Scientifique, n'est pas un simple sous-ensemble
de la Synthèse d'image. En particulier elle demande bien souvent de représenter
des "objets" qui n'ont pas d'images (une particule élémentaire,
par exemple), de répondre à des questions apparemment stupide ("quelle
est la couleur d'une pression ?", voir la figure 5) ou encore de travailler
dans des espaces à plus de
trois dimensions (voir la figure 6).
Figure 05 :
Un
seul et unique champ scalaire bidimensionnel -une matrice- représenté à
l'aide de quatre palettes de couleurs différentes. L'observateur semble avoir
sous les yeux quatre "objets" différents et "orthogonaux" (incompatibles)
entre-eux (1993) !
Figure 06 :
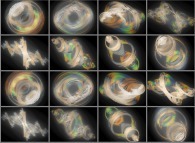Rotation d'une section tridimensionelle d'un ensemble de Julia calculé dans le corps quadri-dimensionnel des quaternions (1995).
Malgré ces difficultés, l'union de la Physique avec les Mathématiques et l'Informatique
(incluant la synthèse d'image) a permis de mettre en œuvre le concept d'Expérimentation Virtuelle.
En effet, quoi qu'elles soient (Réalité Ultime ou "simple"
création de l'esprit humain), les Mathématiques semblent bien être
le langage de la Nature. Ainsi, des plus petites échelles (figure 7) aux
plus grandes (figure 8),
des équations -en général fort complexes-
décrivent l'évolution des systèmes étudiés par les physiciens. Traduites
en programmes, elles peuvent être ensuite résolues à l'aide d'ordinateurs
et leurs solutions présentées aux chercheurs sur un écran. Une boucle de
rétroaction se crée alors entre ces "expérimentateurs virtuels" et
leurs modèles. Ainsi, à condition de disposer de modèles valides,
des expériences autrement irréalisables (comme "jouer" avec l'Univers)
deviennent virtuellement possibles. Malheureusement, l'outil informatique
n'est pas neutre : cela fut déjà signalé en ce qui concerne la mise en images
des résultats numériques (revoir la figure 5). Mais l'ordinateur, machine à la fois finie
et discrète, ne peut pas manipuler correctement les
nombres réels essentiels à la physique ; ignorer cela peut parfois conduire
à des catastrophes
[Plus d'informations à ce sujet].
Figure 07 :
4x3 stéréogrammes d'une variété de Calabi-Yau à l'échelle de Planck (2001).
Figure 08 :
Vision artistique du "Big Bang" (1996).
Donnons deux exemples. Le premier est emprunté à la Mécanique Céleste
: Nos sens semblent nous dire que notre Terre est immobile dans l'espace. Pendant
longtemps cette vision du système solaire (dite géocentrique)
fut considérée comme la réalité et décrite par
le modèle des épicycles de Ptolémée (voir la figure 9).
Mais les progrès accomplis
en matière d'observation et
de mesure eurent raison de cette description. En 1543, le moine polonais
Nicolas Copernic (De revolutionibus orbium caelestium libri VI)
mit le Soleil au
centre du système solaire, faisant par là-même de notre Terre une
planète comme les autres. Puis en 1609, Johannes Kepler (Astronomia Nova)
décrivit la trajectoire des planètes par des ellipses dont l'un des deux foyers
était le Soleil, ainsi que le montre la figure 10. Enfin, en 1687,
Sir Isaac Newton publia ses fameux Philisophiae Naturalis Principia Mathematica dans
lesquels les lois de la mécanique classique firent leur apparition. Cette différence
entre les mouvements subjectif et objectif (problème de mouvement relatif) n'est
évidemment pas propre aux astronomes de la Terre. Il est donc intéressant de
voir le ciel qui serait observé depuis les autres planètes, voire depuis
des points de vue très différents. Ainsi la figure 11 montre l'évolution de la perception du
système solaire en se déplaçant de Pluton au Soleil, alors que la figure 12
fait appel à une planète fictive éloignée du Soleil
et située en dehors du plan de la trajectoire de la Terre (dit plan de l'écliptique).
Plusieurs leçons peuvent être
tirées de ces "expériences virtuelles".
D'une part pour certains systèmes les notions
d'ordre et de désordre peuvent être relatives. En effet, ainsi que le montre
la figure 12,
les trajectoires des planètes du système solaire sont en réalité des ellipses
(la situation est ordonnée et régulière), alors que des trajectoires
complexes, entrelacées et irrégulières peuvent être observées
(la situation semble alors désordonnée et irrégulière). D'autre part,
l'observation des cieux a été au cours des millénaires un moteur essentiel
de notre évolution en ce qui concerne les sciences, la philosophie et
les religions ; où en serait aujourd'hui notre civilisation si notre Terre avait
été située, telle la planète fictive de la figure 12,
en dehors du plan de l'écliptique et plus loin du Soleil (en supposant que la
vie ait pu s'y développer) ?
Figure 09 :
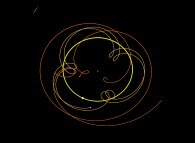Le système solaire géocentrique,
c'est-à-dire dans lequel la Terre est située au centre et donc immobile (corps
bleu). Le mouvement du Soleil (corps jaune le plus gros) est quasiment circulaire,
alors que les planètes (pour simplifier seules Mercure, Vénus et Mars
sont représentées) décrivent des trajectoires beaucoup plus complexes possédant
des boucles dites de rétrogradation.
Figure 10 :
Le système solaire héliocentrique,
c'est-à-dire dans lequel le Soleil est situé au centre et donc immobile. Comme sur la figure 9,
seules les quatre premières planètes -Mercure,
Vénus, la Terre et Mars- sont représentées. Elles décrivent toutes
(la planète bleue -la Terre- y compris) des trajectoires elliptiques (quasiment circulaires).
Figure 11 :
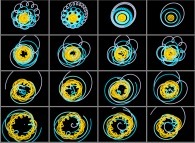En se déplacant du Soleil (image en haut et à droite)
à Pluton (image en bas et à gauche), l'observateur voit les ellipses dites
képleriennes se déformer en des courbes de plus en plus complexes et
entrelacées. Mais tout cela n'est qu'apparence, les planètes continuant
évidemment à décrire leurs trajectoires elliptiques (1997).
Figure 12 :
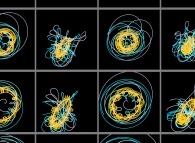Dans le système solaire réel (le plan de l'écliptique apparaît nettement,
alors que celui de Pluton est incliné par rapport à ce dernier) une planète
fictive (elle est coloriée en vert clair afin d'être distinguée facilement
des planètes réelles) est introduite en respectant la troisième lois de
Képler (le carré de la période de révolution est proportionnel au cube
de la mesure du grand axe) -image de gauche-.
Les trajectoires apparentes des planètes
réelles du système solaire telles qu'elles seraient observées depuis la
planète fictive (verte) de la figure précédente. Seul le Soleil semble décrire une
trajectoire régulière (anneau jaune), alors que pour toutes les planètes
le bel ordre des épicycles de Ptolémée disparaît complètement pour
laisser la place à une forme de chaos qualifiable de virtuel. Ainsi pour ce système,
la notion d'ordre est relative (à la position de l'observateur) -image de droite-.
Le second exemple
est "plus proche" de nous et concerne bon nombre de phénomènes naturels.
Autant il est facile de comprendre que la description de phénomènes réguliers
tel le mouvement des planètes du système solaire puisse être de nature mathématique,
autant il est difficile d'imaginer qu'il puisse en être de même, par
exemple, pour les nuages et les montagnes. Et pourtant c'est bien le miracle
accomplit par Benoît Mandelbrot lorsqu'il introduisit la Géométrie Fractale.
Cette dernière permet la mathématisation de la description de ces phénomènes
et donc, par exemple, la production virtuelle de paysages imaginaires
comme le montrent les figures 13 et 14.
Figure 13 :
Le lever du Soleil avec des nuages et un vent violent (1995).
Figure 14 :
La surface de la Lune (1998).
Mais les Mathématiques
ne se contentent pas d'être ce "découvreur de Réalité" illustré
très brièvement ci-dessus, elles sont aussi un fascinant d'outil de création artistique.
D'une part les images issues des expériences virtuelles
peuvent être détournées de leur vocation première et leurs sujets regardés
comme des sources d'inspiration artistique (voir les figures 15 et
16)
et d'autre
part, de la même façon qu'un compas permet de tracer des cercles,
il est possible de définir des outils mathématiques permettant d'engendrer
des objets a priori inimaginables (voir les figures 17
et 18).
Figure 15 :
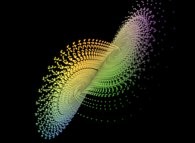L'attracteur de Lorenz (1992).
Figure 16 :
Vision artistique du Système Solaire (1996).
Figure 17 :
Un entrelacs (2009).
Figure 18 :
Un visage "mathématique" basé sur la sphère et la triple bouteille de Bonan-Jeener-Klein (2006).
Jacques Hadamard,
mathématicien français du XX-ième siècle, disait, en
parlant de la pratique des Mathématiques : "généraliser pour simplifier".
Aujourd'hui, je fais mien ce précepte et l'applique aussi à l'art de
la programmation. Et c'est ce vers quoi m'entrainent mes recherches actuelles : définir
des outils mathématiques et informatiques les plus généraux possibles et
ensuite "jouer" avec, afin d'en explorer les potentiels scientifique
et artistique.
LE CONTEXTE INSTITUTIONNEL :
Au tout début des années soixante-dix, la DGT (Direction Générale des Télécommunications du Ministère des Postes et Télécommunications) créait
le STEMME (Service Technique d'Etude des Moyens Modernes d'Enseignement) dirigé par Jean-Gabriel Rémy et installé
à l'ENST (Ecole Nationale Supérieure des Télécommunications) à Paris,
puis au Château de La Martinière 
sur le plateau de Saclay, au cœur d'un parc magnifique 
.
Ce service avait une double vocation : d'une part promouvoir l'utilisation des techniques audiovisuelles
dans le cadre de la formation des agents de télécommunications et d'autre part réaliser des cours.
Pour ce faire il employait de nombreux chargés de programmes et des spécialistes de ces techniques
(prise de vues, prise de sons, montage, banc-titrage,...).
D'autre part il devait étudier l'introduction
de l'informatique dans ces activités, une recherche dont j'ai eu la responsabilité en 1971.
Cela a abouti en seulement quelques années à de nombreux développements originaux réalisés sur une ordinateur T1600
de la société Télémécanique (Grenoble) :
et ce malgré une mémoire centrale de 32 Ko et deux disques d'une capacité de 512 Ko chacun 
!
La TN et la CAAO ne faisaient pas partie initialement du cahier des charges mais ces développements se sont rapidement amplifiés,
même si au début, faire des dessins et des images avec un ordinateur, fut qualifié par certains d'activités de saltimbanque.
C'est alors qu'au milieu des années soixante-dix (1974 ?), l'ENST et l'Ecole Polytechnique décidèrent de créer le LACTAMME
(Laboratoire Commun des Techniques Audiovisuelles et des Moyens Modernes d'Enseignement). De même qu'au STEMME, le LACTAMME
possédait deux missions : d'une part gérer les moyens audiovisuels de ces deux établissements d'enseignement supérieur et d'autre part faire de la recherche
quant à l'introduction de l'informatique dans ces activités. Pour ce faire les moyens et les personnels du STEMME dont je
m'occupai furent transférés en 1977 (?) au LACTAMME, dans les nouveaux locaux de l'Ecole Polytechnique à Palaiseau.
Le T1600 fut remplacé en 1979 (?) par un Solar 16.65 
ordinateur lui-aussi commercialisé
par la société Télémécanique et qui était compatible avec son prédécesseur
tout en ne disposant malheureusement que de la même capacité de mémoire centrale,
mais de plus d'espace disque et d'une horloge un peu plus rapide... Le portage du système d'exploitation et des applications fut donc simple et rapide.
Puis à la fin des années soixante-dix, l'ENST et l'Ecole Polytechnique décidèrent de reprendre en main la gestion de leurs moyens audiovisuels.
Du LACTAMME ne subsista alors que la partie recherche dont je m'occupais. Pendant plusieurs mois, le LACTAMME fut un laboratoire autonome du centre de recherche
de l'Ecole Polytechnique.
Pierre Vasseur, alors initiateur et directeur de ce centre,
fut certainement le premier à comprendre l'importance de la production d'images
par les ordinateurs. En effet, en 1984 s'intallait le C2VR (Centre de Calcul Vectoriel pour la Recherche) 
dans les locaux de l'Ecole Polytechnique,
tandis que se développaient dès 1974 les activités, à la fois scientifiques et industrielles, du CMAP (Centre de Mathématiques APpliquées) sous
l'impulsion de son directeur et fondateur, Jean-Claude Nédélec. Il fut donc alors décidé d'intégrer le LACTAMME au CMAP en 1981.
Mais une bonne partie des équipements du LACTAMME, de même que son personnel, ayant été financés par la DGT (Direction Générale des Télécommunications),
le LACTAMME y conserva un pied en étant aussi rattaché au CNET (Centre National d'Etudes des Télécommunications) à Issy-les-Moulineaux
et au CCETT (Centre Commun d'Etudes de Télévision et Télécommunications) à Rennes,
les directeurs successifs du CNET (en particulier Jean-Pierre Poitevin et Maurice Bernard)
ayant eux-aussi compris l'importance de plus en plus grande de l'image animée et sonore
dans les processus de communications.
Et c'est ainsi que les activités du LACTAMME basculèrent de l'EAO à la visualisation scientifique qui reste aujourd'hui sa spécialité. Mais cela se fit
sans négliger la CAAO, du début des années soixante-dix à aujourd'hui. Cela fut l'occasion de rencontres
de scientifiques
(Claude Bardos,
Claude Basdevant,
Jean-Louis Basdevant,
Michel Cassé,
Françoise Combes,
Adrien Douady,
Etienne Klein,
Benoît Mandelbrot,
Jean-Alain Marck,
Bernard Sapoval,
Jean-Christophe Yoccoz,...),
d'artistes
(Philippe Druillet,
Denis Fadier,
Roberto Matta,
Vera Molnár,
Jacques Rouxel,
Iannis Xenakis,...)
mais aussi de nombreuses expositions et conférences. C'est ainsi, par exemple,
que le 28 février 1978, pour le CNC (Centre National du Cinéma), j'avais fait au Musée Guimet de Paris,
devant le monde du cinéma français, une présentation inédite du numérique dans le
monde de l'image. Cette manifestation avait nécessité l'installation de mon T1600 sur la scène du grand amphithéâtre,
au total une tonne de matériels à déménager...
Et ce fut aussi ma participation en 1986, en tant que conseiller aux images de synthèse
au film Terminus de Pierre-William Glenn,
premier film français faisant appel au numérique en collaboration avec TDI (Thomson Digital Image).
D'ailleurs quelques années après, dans le journal La Recherche en septembre 1987
j'avais publié un grand article sur le "Cinéma Assisté par Ordinateur"
dans lequel j'annonçai à venir l'utilisation de l'IA (Intelligence Artificielle) et la réalisation de films interactifs dans lesquels le spectateur ne serait plus passif :
c'est bien ce à quoi nous assistons aujourd'hui...
LES EXPOSITIONS ET LES PRESENTATIONS :
[Pour avoir peut-être un peu plus d'informations, consulter cette page ou bien celle-ci ou encore celle-là.]
1971
1972
1973
1974
1975
1975/09 Présentation du système SMC au congrès IFIP, Marseille.
1975/10 Démonstration du système SMC au SICOB -Salon des Industries et du COmmerce de Bureau-, Paris La Défense.
1976
1976/07/29 Commentaires de Jean-Gabriel Rémy.
1976/05 IMAGE ET ORDINATEUR, PHOTO-REVUE.
1977
1977/10 Un Système Multimédia Conversationnel, zéro.un.informatique.
1978
1978 Exposition "art et informatique", Savigny.
1978 Exposition "art et informatique" avec "Hommage à Botticelli" et "Divers", IRIA, UNESCO.
1978 Exposition "les plasticiens de l'informatique", Sochaux.
1978 Premier prix au concours "images et ordinateur", Paris.
1978/02/28 Synthèse, traitement et stockage informatique des images, Présentation devant le monde du cinéma français, Musée Guimet, Paris.
1978/09 Computergrafig Galerie : Jean-François COLONNA, ANGEWANDTE INFORMATIK, Herbert Franke.
1979
1979 Exposition "art et informatique", Paris.
1979/05 ARTS ET INFORMATIQUE, MICRO SYSTEMES.
1979/06 ARTS ET INFORMATIQUE, Revue de l'association amicale des ingénieurs de l'ENST.
1979/11 Autour d'un visage, MICRO SYSTEMES.
1980
1980/01 Le système Multimédia Conversationnel : SMC, L'ECHO DES RECHERCHES -CNET-.
1981
1981/03 Un ordinateur qui jongle avec des formes et des couleurs, L'Ordinateur Individuel.
1981/06 LE SYSTEME SMC : la production informatique de films vidéo couleur, Terminal.
1982
1983
1983 Commentaires de Louis Bolliet.
1983/07/21 Commentaires de Pierre Morvan.
1983/10 Commentaires de Jacques Arsac.
1983/12 Exposition Electra, Musée d'Art Moderne de Paris.
1984
1985
1985 Structure fractale d'un front de diffusion, peut-être le premier film vidéo -très basse résolution et d'une durée de 10:45...- sorti en temps réel d'un ordinateur (c'est-à-dire en continu à 25 images par seconde et non pas image par image) [Pour plus d'informations].
1985/03/08 Soutenance de ma Thèse d'État au Centre de Mathématiques Appliquées (CMAP) de l'Ecole Polytechnique (X) en la présence de Jean-Claude Nédélec et de Pierre Vasseur, respectivement directeur du CMAP et des laboratoires de l'X.
1985/05 "Fine work award" au grand prize 1985 de Nikkei Computer Graphics, Japon.
1985/05 Exposition "images synthétiques et calcul numérique", colloque d'analyse numérique de Puy-Saint-Vincent.
1985/07 Participation à l'exposition artistique du SIGGRAPH'85 avec "SUMMER.01", San Francisco, USA.
1986
1986 From Numbers to Pictures : The Computer as an Educational and Artistic Tool, LEONARDO.
1986 DYNAMICS OF THE CREATION OF FRACTAL OBJECTS BY DIFFUSION AND 1/f NOISE, Solid State Ionics.
1986 Conseiller aux images de synthèse pour le film Terminus de Pierre-William Glenn.
1986/04 Une première fresque en hommage à Benoît Mandelbrot, Grand Hall de l'Ecole Polytechnique.
1986/06 Participation au premier festival des arts électroniques de Rennes.
1986/07 Participation à l'exposition "computer & business equipment show", Dublin.
1986/08 Technical Slide Contributor, SIGGRAPH 86, Dallas, USA.
1986/10 Artistic and technical excellence award, International Software Fair, Tokyo.
1986/10 Grand prix du gouverneur d'Osaka, international software fair, Tokyo.
1987
1987 "Une sémiologie graphique appliquée à la simulation numérique", troisième prix au concours Seymour Cray.
1987 Troisième prix au concours dataplotting first international art competition.
1987/05 Participation à la première exposition internationale sur les super-ordinateurs, Santa-Clara USA.
1987/07 Sélectionné pour le art-show du SIGGRAPH'87 avec "RECURSIVE.01", Anaheim, Californie, USA.
1987/09 Le cinéma assisté par ordinateur, La Recherche.
1988
1988 PICTURE SYNTHESIS : AN ESSENTIAL TOOL FOR NUMERICAL EXPERIMENTATION, Computer Physics Communications.
1988/02 Exposition à la bibliothèque centrale de l'X.
1988/08 Technical Slide Contributor, SIGGRAPH'88, Atlanta, USA.
1988/10 Participation à l'exposition "l'image calculée", La Villette, Paris.
1988/11 Médaille baccarat décernée par la société d'encouragement pour l'industrie nationale, Paris.
1989
1989/03 Exposition à la mairie du XIIeme arrondissement de Paris.
1989/06 Publication de l'article Animation of Fractal Objects, Computer Graphics Interface'89, Canada.
1989/08 Technical Slide Contributor, SIGGRAPH'89, Boston, USA.
1989/10 Exposition à la Galerie Arnolfini, Bristol, Grande-Bretagne.
1989/10 Invité à New Delhi dans le cadre de l'année de la France en Inde en compagnie de Jean-Claude Carrière, Michel Cassé, Jacques Rouxel (le père des Shadoks,...).
1989/11 Grand prix au concours "photos de La Recherche", cinquantenaire du CNRS.
1990
1990/03 Exposant, art et informatique, Lyon-La Part Dieu.
1990/06 Artiste sélectionné, Paris Cité.
1990/06 Exposant technique sur le stand BULL, Paris-Cité.
1990/06 Premier prix "imagerie scientifique recherche-université", Paris-Cité.
1990/06/25 Hommage à Benoît Mandelbrot en présence de Jacques Chirac (Maire de Paris), Thétre des Champs-Elysées, Paris-Cité.
1990/08 Technical Slide Contributor -3+1 diapositives-, SIGGRAPH'90, Dallas, USA.
1990/08 Participation à l'exposition artistique du SIGGRAPH'90 avec "Fractal Landscapes", Dallas, USA.
1990/09 Commendation Art and Video Award for technical achievement (pour l'image "Storm"), Ausgraph, Melbourne.
1990/09 Exposition à la maison des ateliers, Forum des Halles, Paris.
1990/10 Exposition à la galerie 172, Faubourg Saint-Honoré, Paris.
1990/11 Participation à "Faites de l'Image'90", Port-de-Bouc.
1990/12 Sélectionné au video-show, FNAC/Informart, La Défense.
1991
1991 Rédaction de Art et Science, 1971-1991.
1991/01/01 Nommé Ingénieur en Chef au Centre National d'étude des Télécommunications (CNET).
1991/09 Présentation de "Along the Border", "Structure fractale d'un front de diffusion" et "Proton" au 41ème congrés international du Cinéma Scientifique, CNAM, Paris.
1991/06 Exposition à la galerie 172, Faubourg Saint-Honoré, Paris.
1991/07 Exposant aux Rencontres de la Photographie d'Arles.
1991/08 Technical Slide Contributor -1 diapositive-, SIGGRAPH'91, Las Vegas, USA.
1991/10 Exposant technique sur le stand BULL, Paris-Cité.
1991/11 Sélectionné pour l'exposition COMPUTER GRAPHICS GALLERY, Alexandra Palace, Londres, Grande-Bretagne.
1991/11 Sélectionné pour l'exposition DATA/DATA, Maryland Art Place, University of Maryland, USA.
1992
1992/05 Exposition à la mairie du XIIème arrondissement de Paris.
1992/07 Technical Slide Contributor -3+1 diapositives, dont une vue stéréoscopique du proton [voir la figure 8 de cette page]-, SIGGRAPH'92, Chicago, USA.
1992/10 20 ans d'images scientifiques, Palais de la découverte.
1992/11 Images d'un autre monde, 8 images et affiche, Palais de Tokyo.
1993
1993/02 Troisième Prix catégorie Recherche pour le film sur le proton, IMAGINA'93.
1993/03 Publication de l'article Un Environnement Portable de Programmation et de Coopération sur Réseau Hétérogène pour le Calcul Scientifique, l'Analyse Visuelle des Résultats et les Tests de Sensibilité à la Précision des Calculs, UNIX'93 Proceedings, Paris.
1993/03 Démonstration de visualisation scientifique stéréoscopique, convention UNIX'93, CNIT, Paris.
1993/05 Exposition, bibliothèque centrale de l'Ecole Polytechnique.
1993/05 Exposition de sculptures numériques, Ecole Polytechnique.
1993/06 "Erreurs d'arrondi et systèmes non linéaires", Forum du Calcul Numérique, CCVR, UNESCO, Paris.
1993/06 Mention honorable (pour le modèle du "chou-fleur"), Ars Electronica'93, Linz, Autriche.
1993/08 Technical Slide Contributor -4 diapositives-, SIGGRAPH'93, Anaheim, USA.
1993/08 Couverture du programme final, SIGGRAPH'93, Anaheim, USA.
1993/08 Publication de l'article The Subjectivity of Computers, Communications of the ACM, Volume 36, Number 8, USA.
1993/10 Exposant sur le stand des labos de l'X, SITEF 93, Toulouse.
1993/11 Participation à l'Artist's Slide Show, FISEA 93, Minneapolis.
1994
1994/02 Publication d'Images du Virtuel, Addison-Wesley France.
1994/03 Exposition de 40 images, "Images du Virtuel", bibliothèque centrale de l'Ecole Polytechnique.
1994/04 Exposition de 40 images, "Images du Virtuel", bibliothèque centrale de l'Ecole Polytechnique.
1994/06 Exposition de 40 images au centre culturel français à Luxembourg dans le cadre du bicentenaire de l'Ecole Polytechnique.
1994/07 Exposition de 40 images à la Commission Européenne à Luxembourg dans le cadre du bicentenaire de l'Ecole Polytechnique.
1994/07 Technical Slide Contributor -3 diapositives-, SIGGRAPH'94, Orlando, USA.
1994/09 Exposition de 40 images au Parlement Européen à Luxembourg dans le cadre du bicentenaire de l'Ecole Polytechnique.
1994/10 Exposition de 40 images à la Médiathèque de Sèvres, "Images du Virtuel".
1994/11 Exposition de 40 images à la Maison de la Culture de Limours, "Images du Virtuel".
1994/11/14 Mise en ligne de mon site Internet A Virtual Machine for Exploring Space-Time and Beyond.
1994/12 Exposition à la mairie du XIIème arrondissement de Paris.
1995
1995/01 Exposition à l'institut francais de Valence, Espagne.
1995/03 Exposition MEDIIART au CCST, Grenoble.
1995/03 Exposition au premier Salon International d'Art Contemporain, Strasbourg.
1995/08 Technical Slide Contributor -5 diapositives-, SIGGRAPH'95, Los Angeles, USA.
1995/10 Publication de l'article Are Autostereograms Useful for Computer Graphics and Scientific Visualization ?, The Visual Computer, Volume 11, Number 7, Japan.
1995/11 Publication de l'article Creativity and Simplicity, The Visual Computer, Volume 11, Number 8, Japan.
1996
1996/01 Un panneau et plusieurs images dans l'exposition sur les fractales de Benoît Mandelbrot, bibliothèque centrale de l'Ecole Polytechnique.
1996/02 Exposition de 50 images au Musée Explora Science Center, Albuquerque, New-Mexico, USA.
1996/03 Exposition organisée par l'ENSEEIHT à l'espace Ecureuil, place du Capitole, Toulouse.
1996/03 Un documentaire diffusé sur Arte.
1996/08 Technical Slide Contributor -2 diapositives-, SIGGRAPH'96, New Orleans, USA.
1989/06 Publication de l'article Kepler, Von Neumann and God [More Rounding-off Error Visualizations], The Visual Computer, Volume 12, Number 7, Japan.
1997
1997/05 Présentation de mon serveur WWW, Ile de Science.
1997/10 Exposant à INTERSCULPT'97, Paris.
1998
1998/01 Exposition de 4 tableaux fractals, "L'Ecole Polytechnique, un patrimoine inattendu", Mona Bismarck Foundation, Paris.
1998/02 "Arret sur Images", Exposition "Explorer l'Espace-Temps" avec Jean-François COLONNA", Cité des Sciences et de l'industrie.
1998/03 Exposition de 19 images, ZoomIN/ZoomOUT, Trieste.
1998/04 Exposition à la mairie du XIIème arrondissement de Paris.
1998/12/21 Rencontre avec le réalisateur Adrien Maben pour l'utilisation d'animations fractales dans une nouvelle version du film Pink Floyd à Pompeï, mais malheureusement, ce projet n'aboutira pas.
1999
1999 Le bug de l'An 2000 approche à grands pas : mes interventions (écrites, radio, télévision,...) se multiplient.
1999/10 Exposition à Fontenay-sous-Bois, Semaine de la Science.
1999/10 Exposition de la Machine Virtuelle à explorer l'Espace-Temps, Semaine de la Science, Maison de la Culture, Fontenay-sous-Bois.
1999/10 Invité au Salon d'Automne, Espace Eiffel-Branly, Paris.
2000
2000 L'attracteur de Lorenz (40mx20m) sur la facade extérieure de la Cité des Sciences, Paris.
2000/09 Exposition au Salon "Physique-Recherche-Industrie", Société Française de Physique, Paris, Porte de Versailles.
2000/10 Exposition de 7 images lors de la Fête de la Science, Ministère de la Recherche, Paris.
2000/10 Exposition lors de la Fête de la Science, Ministère de la Recherche.
2000/10 Invité au Salon d'Automne, Espace Eiffel-Branly, Paris.
2000/11 Exposition "On ne voit bien qu'avec le coeur", Académie des Sciences, Sénat.
2000/11 Exposition d'images fractales, Hotel de Ville, Marcoussis.
2001
2001/03 Publication de l'article Pour la Sauvegarde du Patrimoine Virtuel De l'Humanité, "An 2001, Les Enjeux du XXIème Siècle", Université des Sciences et des Technologies de Lille.
2001/05 Exposition de sequences vidéos, Média Village, Paris.
2001/06 Exposition Images, Cité des Sciences et de l'Industrie, Paris.
2001/06 Exposition La Mosaïque Mystérieuse, Cité des Sciences et de l'Industrie, Paris.
2001/11 Invité au Salon d'Automne, Espace Auteuil, Paris.
2002
2002/04 Exposition d'images et de vidéos, Galerie de l'ADAC, 21 rue Saint-Paul, 75004 Paris.
2002/06 Exposition d'images, Dourdan.
2002/10 Participation à l'exposition "Effets d'optique", Mairie de Palaiseau.
2002/11 Exposition "Art et Science" dans le cadre de la "Journée mondiale de la science au service de la paix et du développement", UNESCO, Paris.
2002/11 Invité au Salon d'Automne, Espace Auteuil, Paris.
2003
2003/10 Participation à l'exposition "Effets d'optique", Ecole Polytechnique.
2003/04 Exposition d'images fractales, ENST Bretagne.
2003/06 Exposition de Stéréogrammes et d'Autostéréogrammes, Cité de la Géométrie, Maubeuge.
2003/06 Exposition sur la géométrie fractale, Salon des Jeux et de la Culture Mathématique, Paris.
2003/10 Exposition d'images, Savigny-sur-Orge.
2004
2004/07 Exposition, bibliothèque centrale de l'Ecole Polytechnique.
2004/11/13 Remise de 25 de mes œuvres à Benoît Mandelbrot à l'occasion de son quatre-vingtième anniversaire, Faculté de Médecine Necker, Paris.
2005
2005 Exposition "Art & Science", 2005 Année de la Physique, Ecole Polytechnique.
2005/01 Exposition "Mathématiques et Art", Bibliothèque de l'Institut Henri Poincaré, Paris.
2005/05 Exposition "Art & Science", Salon d'honneur de l'Ecole Polytechnique.
2005/06 Exposition "Art & Science", Science and Art, Rutgers, State University of New Jersey, USA.
2005/08 Exposition groupée "Mathématiques et Art", Bibliothèque de l'Ecole Polytechnique, Paris.
2005/09 Décoration de la Salle Auguste Detœuf, Ecole Polytechnique.
2006
2006/09 Exposition "Art & Science", Espace Mendès France, Poitiers.
2006/10 Exposition "Art & Science", Lycée Fragonard, L'Isle-Adam.
2006/09 Exposition "Art & Science", Mediathèque George Sand, Mairie de Palaiseau.
2006/02 Exposition "Art & Science", Colloque "Méso Ile de France Sud", Ecole Normale Supérieure de Cachan.
2006/05 Exposition sur le stand du CNRS, Salon de la Culture et des Jeux Mathématiques, place Saint Sulpice, Paris.
2006/06 Exposition "Art & Science", Mairie de Palaiseau.
2006/09 Diaporama de 82 images fractales, Amphithéatre Pierre Faure, remise de la Légion d'Honneur à Benoît Mandelbrot, Ecole Polytechnique.
2006/09 Exposition de 12 images fractales, remise de la Légion d'Honneur à Benoît Mandelbrot, Salon d'Honneur de l'Ecole Polytechnique.
2006/10 Exposition "Art & Science", Orangerie, Soisy sous Montmorency.
2007
2007/01 Exposition "Art & Science", Lycée Lavoisier, Paris.
2007/01 Exposition "Art & Science", MJC de Corbeil-Essonnes.
2007/03 Exposition "Art & Science", Paris XII, Créteil.
2007/09/28 Exposition "Art & Science", la Nuit des Chercheurs, Ecole Polytechnique.
2008
2008/02 Exposition "Art & Science", Galerie "Air Libre", Evry.
2008/05/05 Conférence à la prison de Fleury Mérogis sur les Mathématiques, l'art,...
2008/06/23 Conférence à la prison de Fleury Mérogis sur les Mathématiques, l'art,...
2008/09 "A quoi servent les Mathématiques ?", la Nuit des Chercheurs, Ecole Polytechnique.
2008/11 Exposition de 3 tableaux et diaporama géant, Ville Européenne des Sciences, Grand Palais de Paris.
2008/12 Exposant à l'exposition "Algorists 2008" au KITP de l'Université de Santa Barbara.
2009
2009/09 "A quoi servent les Mathématiques ?", la Nuit des Chercheurs, Ecole Polytechnique.
2009/10 Festival Math En Rue, Diaporama géant sur la façade de l'Hotel de Ville de Bruxelles.
2009/10 Exposition "Art & Mathématiques", fondation Peugeot, atelier Z, 75017 Paris.
2010
2010/03 Exposition "Art & Science", Colloque Art et Science, Université de Versailles-Saint Quentin, Versailles.
2010/06 Exposition "Art & Mathématiques", IHP, 75006 Paris.
2010/09 "A quoi servent les Mathématiques ?", la Nuit des Chercheurs, Ecole Polytechnique.
2010/09 Exposition "Art & Science", la Nuit des Chercheurs, Ecole Polytechnique.
2010/09 Exposition, bibliothèque centrale de l'Ecole Polytechnique.
2010/09/24 Projection géante "Art & Science", la Nuit des Chercheurs, Ecole Polytechnique.
2011
2011/03 Une seconde fresque en hommage à Benoît Mandelbrot, Grand Hall de l'Ecole Polytechnique.
2011/03 Une exposition d'images en hommage à Benoît Mandelbrot, Grand Hall de l'Ecole Polytechnique.
2011/09 "A quoi servent les Mathématiques ?", la Nuit des Chercheurs, Ecole Polytechnique.
2012
2012/02 Exposition de plusieurs oeuvres à la Mairie du cinquième arrondissement, "Art et Mathématiques".
2012/09 "A quoi servent les Mathématiques ?", la Nuit des Chercheurs, Ecole Polytechnique.
2012/11 Trois images de type 'NCOR' lors d'un hommage à Henri Poincaré, Sorbonne, Paris.
2013
2013/02 Une trentaine d'images fractales, Mediathèque de Sèvres.
2013/09 "A quoi servent les Mathématiques ?", la Nuit des Chercheurs, Ecole Polytechnique.
2013/09 Exposition Bibliothèque Centrale de l'Ecole Polytechnique.
2013/09/27 Exposition d'anaglyphes, la Nuit des Chercheurs, Grand Hall, Ecole Polytechnique.
2014
2014/10 "A quoi servent les Mathématiques ?", Fête de la Science, Ecole Polytechnique.
2015
2015/01 Exposition de 20 images, Bibliothèque Centrale de l'Ecole Polytechnique.
2015/03 Exposition de 20 images, Lycée Louis le Grand, Paris.
2015/03 Exposition de 2 images, "Les Mathématiques vivantes et visuelles", Centre International de Rencontres en Mathématiques (CIRM), Marseille.
2015/10 "A quoi servent les Mathématiques ?", Fête de la Science, Ecole Polytechnique.
2015/10/10 Exposition de 12 images, Fête de la Science, Grand Hall, Ecole Polytechnique.
2016
2017
2018
2018/03 Exposition de 6 euvres, Mairie du cinquième arrondissement, "Art et Mathématiques".
2018/03 Exposition de 12 oeuvres, Musée Galatasaray et centre Culturel Français, Istanbul, Turquie.
2018/10/13 Exposition de 14 images, Fête de la Science, Grand Hall, Ecole Polytechnique.
2018/11 Exposition d'une image, UNESCO, Paris.
2019
2019/10/12 Exposition de 19 images, Fête de la Science, Grand Hall, Ecole Polytechnique.
2020
2020/01 Exposition de 19 images, Grand Hall, l'Opéra de Massy.
2020/02 Exposition d'une quarantaine d'images, Mairie du cinquième arrondissement de Paris.
2021
2022
2022/02 Exposition Art et Mathématiques, Institut des Hautes Etudes Scientifiques (IHES), Bures-sur-Yvette.
2022/02/10 Dépôt à RCM GALERIE de 212 (?) dessins originaux des années 1970, Paris.
2023
2024
2024/01/10 Don de six tableaux à l'Institut Henri Poincaré (IHP) et remise à Sylvie Benzoni, sa directrice, Paris.
2024/02/26 Dépôt à RCM GALERIE d'un stéréogramme d'une variété de Calabi-Yau suivant le procédé Bonnet, 08/2009, Paris.
2024/03/07 Dépôt à RCM GALERIE de 120 tirages Polaroîds en couleurs des années 1970, Paris.
2024/03/07 Dépôt à RCM GALERIE de 20 anaglyphes, 09/2012, Paris.
2024/03/07 Dépôt à RCM GALERIE de la diapositive géante "La Génèse", 1976, Paris.
Copyright © Jean-François COLONNA, 2009-2024.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2009-2024.
