Quelques Remarques concernant la Nature des Mathématiques






Jean-François COLONNA
[Contact me]

www.lactamme.polytechnique.fr

CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France

[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[Real Numbers don't exist in Computers and Floating Point Computations aren't safe. [Les Nombres Réels n'existent pas dans les Ordinateurs et les Calculs Flottants ne sont pas sûrs.]]
[N'oubliez pas de visiter Une Machine Virtuelle à Explorer l'Espace-Temps et au-delà où vous trouverez plus de 10.000 images et animations à la frontière de l'Art et de la Science]
(Site WWW CMAP28 : cette page a été créée le 12/11/2009 et mise à jour le 03/10/2024 17:09:57 -CEST-)



(Article paru dans la revue Tangente, 12/2009)


Mots-Clefs : A2M, An 2000, Bogue, Bug, Bugix, Millenium Bug, Year 2000 Problem, Y2K, Y2K Bug, Anaglyphes, Art et Science, Autostéréogrammes, Chaos Déterministe, Création Artistique, Entrelacs, Erreurs d'arrondi, Expérimentation Virtuelle, Génie Logiciel, Géométrie Fractale, Infographie, Mathématiques, Mécanique Céleste, Mécanique Quantique, Physique, Sensibilité aux Erreurs d'Arrondi, Simulation Numérique, Stéréogrammes, Synthèse de Phénomènes Naturels, Synthèse de Texture, Visualisation Scientifique, Voyage Virtuel dans l'Espace-Temps.



Les progrès en Mathématiques dites pures se font en général grâce à des problèmes posés, tels des défis, par un mathématicien à la communauté. La plupart du temps, pour ne pas dire toujours, ces questions sont abstraites, souvent incompréhensibles pour le commun des mortels et sans rapport apparent avec la Réalité tangible. Un exemple récent, qui fit la une des journaux, fut la démonstration du Grand Théorème de Fermat achevée par Andrew Wiles après plus de trois siècles de tâtonnements, d'erreurs et d'efforts. Et malgré l'immensité de l'entreprise et le succès rencontré, voici un résultat de peu d'utilité alors que le tortueux chemin parcouru pour son obtention fut incroyablement riche en développements et en rencontres fortuites. Ainsi présentées, les Mathématiques sembleraient alors n'être qu'un "simple" jeu de l'esprit guère plus utile au quotidien que les échecs.

Pourtant depuis deux mille ans et encore plus à partir du dix-septième siècle avec les travaux de Galilée, les Mathématiques sont considerées comme le langage avec lequel sont écrites les lois de la Nature. Pendant longtemps les modèles conçus par les physiciens furent principalement descriptifs. Ce fut ainsi le cas des épicycles de Ptolémée qui décrivait le mouvement du Soleil et les rétrogradations des planètes alors connues. Les progrès concomitants des Mathématiques et des appareils d'observation et de mesure (du temps tout particulièrement) permirent l'émergence de modèles tout à la fois descriptifs et prédictifs. Les Mathématiques devinrent alors, à côté du microscope et du télescope, un "instrument d'observation" révolutionnaire qui nous révèle chaque jour de nouvelles et mystérieuses facettes de notre Univers (voir la figure 1). Aujourd'hui les résultats obtenus, en particulier dans le cadre de la Mécanique Quantique et de la Relativité Générale, sont d'une précision époustouflante (tout comme ceux de nombreuses expériences de Physique...) et les "dix chiffres après la virgule" ne sont pas rares !

[Pour plus d'informations sur les Mathématiques]

Mais ces succès ne font que rendre plus mystérieuses la nature profonde des Mathématiques et la cause de leur "redoutable efficacité" (Eugène Wigner, 1960). Que sont donc les (nos ?) Mathématiques ? Deux réponses apparemment inconciliables peuvent être formulées : soit elles ne sont "que" le fruit de notre esprit, soit elles existent indépendamment de nous. Formulé différemment : le mathématicien est-il comme Gustave Eiffel qui imagina la tour éponyme ou bien comme Christophe Colomb (ou un viking anonyme...) qui découvrit l'Amérique ? Le mathématicien est-il un créateur (c'est-à-dire celui qui tire du néant) ou bien un explorateur (celui qui parcourt en observant) ? Examinons successivement ces deux positions.



Le mathématicien créateur :

Les Mathématiques sont ici le fruit de l'imagination des mathématiciens et d'elle-seule. Leur efficacité peut alors émerger d'une part du fait que dans le cortex, les structures responsables des sens créent progressivement des modèles de notre environnement (au sens large) ; ces structures sont identiques -voire sont les mêmes- à celles qui nous permettent de créer (mais qu'est-ce que la création ?). Il est d'ailleurs possible de conjecturer qu'en l'absence de perceptions sensorielles, il n'y aurait pas de conscience et donc pas d'imaginaire. Il est dès lors logique de considérer que dans ce contexte les Mathématiques (nos Mathématiques alors !) sont contraintes par nos modèles sensoriels (même si elles nous permettent d'aller beaucoup plus loin que notre intuition), d'où l'adéquation. Cela pourrait alors expliquer que, tel Monsieur Jourdain qui disait de la prose sans qu'il en sût rien, le mathématicien pur fasse souvent (toujours ?) de la Physique sans le savoir (ainsi, par exemple, les groupes d'Evariste Galois sont aujourd'hui au cœur de la Physique et sans les variétés de Bernhard Riemann la Relativité Générale d'Albert Einstein n'aurait peut-être pas vu le jour en 1915).

D'autre part notre environnement, proche comme lointain, n'est pas aléatoire : des structures, des symétries, des invariances,... dans le temps comme dans l'espace, sont identifiées. Une ou plusieurs façons de "compresser", de "résumer" ces régularités doivent alors être envisageables (par analogie, il est possible de compresser les images numériques grâce au JPEG ou encore aux ondelettes parce qu'elles ne sont pas aléatoires). Les Mathématiques seraient alors un langage (parmi d'autres) de compression d'observations. Ceci est alors à rapprocher de la notion de complexité algorithmique qui permet de caractériser la complexité d'un ensemble (de nombres par exemple) par la taille du plus petit programme permettant de le reproduire. Les Mathématiques seraient donc un langage de programmation et, suivant le principe du rasoir d'Occam (tout à la fois principe d'économie et de simplicité), un modèle serait le programme le plus simple (qui n'est pas nécessairement le plus court dans ce contexte !) reproduisant un certain fragment de Réalité, dans la limite des observations actuelles. Donnons un exemple avec la suite suivante résultant d'une certaine observation : 
                    {0,2,4,6,8,...,28,30}.
De nombreux programmes (c'est-à-dire des modèles mathématiques) permettent de la reproduire et par exemple : 
                    M1 - Calcul des entiers naturels pairs                                             : {n | n=0 ; {n=n+2} ; n<=30},
                    M2 - Calcul du double des entiers naturels                                         : {s | n=0 ; {s=2*n ; n=n+1} ; n<=15},
                    M3 - Calcul de la partie entière d'un certain polynôme                             : {PartieEntière(s) | n=0 ; {s=2*n + 0.004*n2 ; n=n+1} ; n<=15},
                    (...)
                    Mi - Calcul de la valeur absolue des zéros triviaux de la fonction Zêta de Riemann : {mod(z) | Zeta(z)=0, Im(z)=0},
                    (...)
Il est clair qu'en l'absence d'informations supplémentaires le modèle M1 est le plus simple. Mais ce n'est pas parce qu'il permet de reproduire exactement et de la façon la plus économique qui soit la suite {0,2,4,6,8,...,28,30} qu'il correspond aux motivations et aux intentions de son "créateur" qui pourront à jamais rester inaccessibles. Et c'est là une difference importante entre les Mathématiques et la Physique : les vérités mathématiques (en particulier celles qui ont déjà été démontrées) sont éternelles alors que celles de la Physique sont précaires. Il suffit qu'un certain progrès prolonge la suite précédente sous la forme : 
                    {0,2,4,6,8,...,28,30,33}
pour que le modèle M1 soit supplanté par M3, en notant qu'alors M2 en devient une bonne approximation (en négligeant le terme 0.004*n*n), tout en réfutant M1 et Mi (les excluant ainsi de la liste des modèles possibles).

Les Mathématiques seraient alors relatives à nos structures cognitives, à notre évolution culturelle et à notre environnement en notant bien que, malgré le principe cosmologique (il n'y a pas de point et de direction privilégiés dans l'Univers), notre Terre, sans être unique (fort probablement), est un lieu rare, particulier et privilégié (puisque nous y sommes en tant qu'observateur !) et que cela a nécessairement influencé, voire certainement distordu, notre appréhension de la Réalité.



Le mathématicien explorateur :

Les Mathématiques sont ici les mêmes aux "quatre coins de l'Univers". Mais il y a deux façons de comprendre cela : soit les Mathématiques ne sont "que" Le Langage (unique) de description de l'Univers, mais contrairement à la définition précédente, elles ne sont plus relatives mais absolues et donc indépendantes de l'observateur (nous en particulier). Elles résident alors hors de notre temps et de notre espace, en un "lieu platonicien" auquel notre conscience a accès et à l'intérieur duquel nous avançons progressivement. Mais où est-il (question embarassante, mais pas plus que celle de savoir où est notre Univers !) et comment se fait la connexion ?

Soit, et c'est là une conception encore plus audacieuse (c'est en particulier celle de Max Tegmark), les Mathématiques sont (et elles seules) la Réalité. Alors, en elles et de par leur complexité, émergent ici et là des "groupes" de structures conscientes (nous en particulier) qui subjectivement se considèrent chacun comme vivant dans leur monde physique réel, bien qu'étant en fait virtuel. Dans cette réalité mathématique infinie, de nombreux mondes virtuels naîtraient ainsi, chacun avec leurs lois et leurs contenus propres. Mais la question se pose alors du statut des axiomes qui sont à la base des Mathématiques : en effet, non démontrables, ils sont imposés par la nécessité, la logique et la cohérence nécessaire de l'édifice. Ils peuvent nous sembler arbitraires et "anthropiques", mais d'autres "jeux" d'axiomes pourraient exister dans d'autres régions de cette réalité platonicienne dont la totalité nous échapperait...

Cela est aussi en relation avec la notion de Multivers qui est une tentative actuelle pour comprendre les valeurs très particulières des constantes fondamentales de Notre Physique et donc les "conditions initiales" très improbables du Big Bang. En 1543, Copernic nous révéla que notre Terre n'était qu'une planète comme les autres, puis nous avons découvert que notre Soleil n'était qu'une étoile comme les autres, puis que notre Voie Lactée n'était qu'une galaxie comme les autres. Notre Univers ne serait-il donc pas un univers comme les autres ? De nombreux (une infinité ?) d'univers coexisteraient à l'intérieur du Multivers, avec chacun leurs lois et leurs contenus et ainsi, si toutes les conditions initiales possibles sont représentées, notre Univers avec les siennes si spécifiques doit nécessairement exister ! Cela nous rappelle les tentatives faites par Kepler au dix-septième siècle pour justifier les positions relatives des planètes du système solaire alors connues, à l'aide des solides platoniciens. Cette quête était vouée à l'échec car leurs trajectoires sont en fait étroitement liées aux conditions initiales, de nature contingente, de formation du système solaire. Pourquoi notre système solaire est-il comme il est ? "Tout simplement" parce que quasiment toutes les configurations de systèmes planétaires doivent exister (y compris donc le nôtre), ce que les découvertes de plus en plus nombreuses d'exo-planètes semblent confirmer !

Considérer que les Mathématiques sont la seule Réalité permet ainsi d'engendrer un Multivers, mais aussi de répondre à une interrogation d'un niveau supérieur : pourquoi les lois de la (notre) Nature sont-elles celles que nous mettons en évidence et en particulier pourquoi les équations différentielles y règnent-elles en maître ? La réponse pourrait être "tout simplement" que notre Univers a émergé d'une infime partie de la région des Mathématiques où elles "vivent".

Une variante de cette position doit être envisagée parce qu'actuellement irréfutable (c'est-à-dire dont la fausseté ne peut être prouvée), même si en appliquant de nouveau le principe du rasoir d'Occam, elle peut paraitre extravagante. Notre Univers ne serait-il pas le résultat d'une simulation ? Il ne s'agirait là ni plus ni moins que d'un jeu vidéo et nos Mathématiques pourraient être le langage de programmation que nous, êtres conscients mais simulés, découvririons progressivement. Mais alors d'autres questions encore plus épineuses surgissent : dans quel Univers se déroule cette simulation et qui en est le programmeur ? Cet Univers est-il lui-aussi simulé ? Allons-nous ainsi empiler une infinité de "tortues" les unes sur les autres ? Malgré tous ses défauts, cette solution présente l'avantage de réintroduire scientifiquement et explicitement les questions fondamentales de la Création et de l'Existence.



Alors, le mathématicien créateur ou explorateur ?

Un contact avec d'hypothétiques intelligences extra-terrestres, si tant est qu'un dialogue équitable fut possible, lèverait certainement un petit coin du voile (dans Contact, roman de science-fiction publié en 1985, Carl Sagan faisait implicitement l'hypothèse platonicienne, en donnant, en particulier, la vedette aux nombres premiers et à pi [01]).

Mais peut-être la réponse est-elle que le mathématicien est à la fois créateur et explorateur : certaines structures, probablement parmi les plus élémentaires, existeraient indépendamment de nous (les nombres entiers ordinaux et cardinaux, par exemple), alors que d'autres seraient notre œuvre (un peu comme il existe dans l'Univers un certain nombre de molécules naturelles et que nos chimistes en ont créé de nouvelles à partir des éléments de base que sont les atomes). N'était-ce d'ailleurs pas la position de Leopold Kronecker qui, en 1891, avait déclaré : "Dieu a fait les nombres entiers, tout le reste est l'œuvre de l'homme".

Les réponses se feront peut-être attendre éternellement parce que la Réalité et la connaissance qu'il est possible d'en avoir, sont à mon sens de nature fractale. Souvenons-nous de la remarque de Lord Kelvin qui, à la fin du dix-neuvième siècle, imaginait la Physique achevée : il ne restait "plus" qu'à ajouter quelques décimales aux constantes universelles et à éclaircir un "petit point de détail" : celui du corps noir (et la suite est bien connue : c'est la révolution de la Mécanique Quantique...) ! N'est-ce pas là le propre d'un objet fractal que de nous échapper toujours davantage : tout nouvel agrandissement de l'une de ses parties ne nous révèle-t-il pas un nouvel univers de formes et de détails (voir la figure 2) ?

Ces limites et ces insondables mystères doivent être acceptés et ne doivent surtout ni briser notre bel élan d'insatiable curiosité, ni interrompre cette ultime forme d'aventure moderne qu'est la recherche en Mathématiques !



FIGURE 1 :

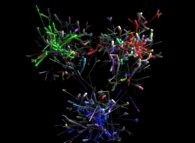
L'infiniment petit.  
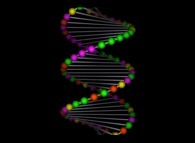La Vie et l'Homme, la Terre est son berceau.  
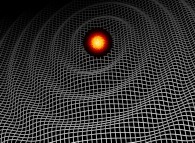
L'infiniment grand.

La Physique aujourd'hui, de 1.6 10-35 mètre (échelle de Planck) à 8.8 1026 mètres (horizon cosmologique) et au-delà ("dans" le(s) Multivers).


FIGURE 2 :



Zoom sur une représentation tridimensionnelle de l'ensemble de Mandelbrot, immergé dans des nuages fractals, avec visualisation des arguments dits de sortie.





Copyright © Jean-François COLONNA, 2009-2024.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2009-2024.