Les Calculs Flottants sont-ils Fiables ?
ou
Un Ordinateur "sait-il" Bien Calculer ?
CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France
france telecom, France Telecom R&D
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[N'oubliez pas de visiter Une Machine Virtuelle à Explorer l'Espace-Temps et au-delà où vous trouverez plus de 10.000 images et animations à la frontière de l'Art et de la Science]
(Site WWW CMAP28 : cette page a été créée le 22/03/2004 et mise à jour le 16/01/2026 15:00:58 -CET-)
[in english/en anglais]
Mots-Clefs : Floating Point Numbers, Nombres Flottants, Rounding-off Errors, Erreurs d'arrondi.
Un ordinateur (quelqu'en soit le type) est une machine tout à la
fois finie (elle possède une capacité mémoire limitée) et
"discrète" (l'information doit être échantillonnée et quantifiée avant tout
traitement numérique). Ces deux caractéristiques sont malheureusement
trop souvent oubliées, ce qui peut être alors la source de
désagrements (euphémisme...).
A titre d'exemple du caractère fini
des ordinateurs, étudions la suite définie par :
S = 0
0
S = S + 1
n n-1
Quelle est donc la valeur de S(n) ? La réponse "mathématique"
est évidemment :
S = n
n
Malheureusement, la réponse "informatique" peut être très
différente, ainsi que le montre le programme suivant,
destiné à calculer numériquement cette valeur :
#define N "une certaine valeur positive et entière..."
main()
{
int n;
float sigma=0;
for (n=1 ; n <= N ; n++)
{
sigma = sigma + 1.0;
}
printf("\n somme calculee = %f",sigma);
}
Il donne systématiquement la valeur 16777216
(alors qu'il devrait évidemment donner la valeur N en l'absence de ce problème...)
pour toute valeur de N supérieure ou égale a 16777216.
En ce qui concerne le caractère discret
des ordinateurs, la conséquence immédiate est, en
toute généralité, l'impossibilité
de manipuler les nombres Réels. Ces derniers n'existent tout
simplement pas dans l'univers numérique. Ils sont très grossièrement
approchés par les nombres dits flottants.
A cause de cela, des constantes apparemment très simple (par exemple
4095.1 et 4096.1 qui seront utilisées ci-après)
ne sont pas représentables exactement en machine.
De plus, pour ces nombres, les opérations arithmétiques élémentaires
ne sont en général pas internes.
Lors de chacune d'entre-elles,
une erreur d'arrondi est introduite ;
celle-ci est alors la cause
de la perte de la propriété d'associativité
de l'addition et surtout
de celle de la multiplication (notons que dans ces conditions,
la multiplication n'est alors plus distributive par rapport a l'addition).
Ainsi, par exemple, en simple précision (c'est-à-dire sur 32 bits
et ce afin de simplifier l'impression hexa-décimale des résultats
-voir la même expérience en double précision 64 bits-),
le programme suivant (ou la fonction 'MUL' est destinée a forcer l'ordre
des multiplications) :
float MUL(x,y)
float x,y;
{
return(x*y);
}
main()
{
float A=3.1,B=2.3,C=1.5;
float X,Y;
X=MUL(MUL(A,B),C);
Y=MUL(A,MUL(B,C));
printf("\n (%f x %f) x %f = %f\n",A,B,C,X);
printf("\n %f x (%f x %f) = %f\n",A,B,C,Y);
}
donne comme résultats :
(3.10 * 2.30) * 1.50 = 10.695000 = 0x412B1EB8
#### #
et :
3.10 * (2.30 * 1.50) = 10.694999 = 0x412B1EB7
#### #
ce qui constitue deux résultats différents. On notera au passage,
que d'une part l'écriture de ce programme pourrait être bien plus
concise, mais que s'il est ainsi redigé, c'est
dans l'espoir de contrôler le plus possible le code généré par
le compilateur, aucune optimisation n'étant demandée
évidemment. D'autre part, l'expérience peut être refaite
avec d'autres langages de programmation (par exemple java
ou le programmeur maitrise l'ordre d'évaluation des opérations,
mais est-ce bien vrai ?) ;
elle produit évidemment le même phénomène...
L'expérience précédente pourrait être tentée à l'aide du programme :
main()
{
float A=3.1,B=2.3,C=1.5;
float X,Y;
X=(A*B)*C;
Y=A*(B*C);
printf("\n (%f x %f) x %f = %f",A,B,C,X);
printf("\n %f x (%f x %f) = %f",A,B,C,Y);
}
Lorsqu'elle ne montre pas le phénomène ici décrit,
deux explications, au moins, peuvent être avancées :
- le compilateur utilisé transforme la simple
simple précision 32 bits
en double précision 64 bits
à l'insu de l'utilisateur,
- le compilateur utilisé compile de façon similaire
les expressions (AxB)xC et Ax(BxC),
supposant la propriété d'associativité satisfaite.
Il conviendra alors d'augmenter le nombre de décimales
des trois variables 'A', 'B' et 'C', ou
encore d'essayer un autre compilateur, ou enfin
évidemment d'exploiter le programme utilisant la fonction 'MUL'...
Il convient de noter que la propriété d'associativité de l'addition
est donc, elle aussi perdue, mais qu'elle se manifeste
plus rarement et de façon moins grave au niveau de ses consèquences.
Ainsi, par exemple, en simple précision (c'est-à-dire sur 32 bits
et ce afin de simplifier l'impression hexa-décimale des résultats
-voir la même expérience en double précision 64 bits-),
le programme suivant
(ou la fonction 'ADD' est destinée à forcer l'ordre des additions) :
float ADD(x,y)
float x,y;
{
return(x+y);
}
main()
{
float A=1.1,B=3.3,C=5.5;
float X,Y;
X=ADD(ADD(A,B),C);
Y=ADD(A,ADD(B,C));
printf("\n (%f x %f) x %f = %f\n",A,B,C,X);
printf("\n %f x (%f x %f) = %f\n",A,B,C,Y);
}
donne :
(1.10 + 3.30) + 5.50 = 9.900000 = 0x411E6666
# #
ce qui est différent de :
1.10 + (3.30 + 5.50) = 9.900001 = 0x411E6667
# #
[Evidemment une anomalie similaire peut-être constaté avec la distributivité de la multiplication sur l'addition]
Le seul aspect positif de ce "dysfonctionnement" est qu'il permet de
nous rappeler (montrer ?) qu'un ordinateur, sauf cas particuliers
(celui des petits nombres entiers, par exemple),
ne calcule pas exactement !
Lors de l'étude de problèmes non linéaires,
tout cela peut avoir des conséquences absolument
dévastatrices. A titre d'exemple, le calcul de l'itération
(dite Dynamique de Verhulst ) :
2
X = (R+1)X - RX
n n-1 n-1
qui est équivalent à la succession des calculs suivants :
X
0
|
---------------
| |
\|/ \|/
' '
2
X = (R+1)X - RX
1 0 0
|
---------------
| |
\|/ \|/
' '
2
X = (R+1)X - RX
2 1 1
|
---------------
| |
\|/ \|/
' '
2
X = (R+1)X - RX
3 2 2
|
---------------
| |
\|/ \|/
' '
etc...
peut se faire par le programme élémentaire, voire simpliste,
donné de façon très détaillée ci-après (sont mises en gras, les lignes
réellement essentielles) :
main()
{
double R=3.0;
double X=0.5;
int n;
for (n=0 ; n <= 80 ; n++)
{
if ((n%10) == 0)
{
printf("\n iteration(%04d) = %9.6f",n,X);
}
else
{
}
X = (R+1)*X - R*X*X;
}
}
donne sur une O200 Silicon Graphics (processeur R10000),
sous IRIX 6.5.5m et cc 7.2.1,
les résultats suivants en fonction des options d'optimisation :
O200 Silicon Graphics (R10000, IRIX 6.5.5m, cc 7.2.1) :
option '-O2' option '-O3'
X(00) = 0.500000 0.500000
X(10) = 0.384631 0.384631
X(20) = 0.418895 0.418895
X(30) = 0.046399 0.046399
X(40) = 0.320184 0.320192
X(50) = 0.063747 0.059988
X(60) = 0.271115 1.000531
X(70) = 1.328462 1.329692
X(80) = 0.817163 0.021952
Il est facile de calculer simultanément les extrema
de tous les résultats de tous les calculs intermédiaires
lors de chaque opération arithmétique élémentaire.
Le minimum trouve est strictement positif et inférieur à 1,
sans être petit par rapport au plus petit nombre positif représentable.
Le maximum, quant à lui, vaut quelques unités.
Il n'y a donc jamais de calculs élémentaires au cours desquels
seraient combinés deux nombres d'ordres de grandeur très
différents et donc incompatibles avec la représentation
flottante. Il convient de noter au passage que ce dernier problème peut
être lui aussi la cause de phénomènes "ennuyeux" ; ainsi, à titre
d'exemple, en double précision 64 bits,
additionner 1 à 1e16 ("10 à la puissance 16") est sans effet,
ce qui conduit à l'égalité paradoxale suivante :
16 16
10 + 1 = 10
En ce qui concerne l'influence éventuelle de la syntaxe,
voici une expérience troublante effectuée (avec R = 3.0) en Java
(langage réputé pour son caractère
write once, run everywhere...) avec des variables
déclarées avec le type double :
un même programme calcule sur deux machines différentes
et de cinq façons différentes (mais équivalentes mathématiquement)
l'itération précédente. Voici les résultats obtenus :
O200 Silicon Graphics (processeur R10000, IRIX 6.5.5m, Java) :
(R+1)X-R(XX) (R+1)X-(RX)X ((R+1)-(RX))X RX+(1-(RX))X X+R(X-(XX))
X(0000) = 0.5 0.5 0.5 0.5 0.5
X(0500) = 1.288736212247168 0.007057813075738616 1.2767485100695732 1.246534177059494 0.03910723014701789
X(1000) = 1.3327294162589722 0.916560711983132 1.207710752523091 0.27770146115891703 0.26663342726567785
X(1500) = 1.1448646685382955 0.4481000759915065 0.3102077001456977 0.015374092695375374 0.9841637252962943
X(2000) = 1.0548628914440754 0.896126931497168 0.6851138190159249 0.009229885271816535 0.3860923315999224
X(2500) = 1.292802584458599 0.06063433547953646 1.174118726001978 0.6922411856638806 0.020878761210912034
X(3000) = 1.0497821908090537 0.0219606878364607 1.3287403237319588 0.11354602472378028 0.13270749449424302
X(3500) = 0.8115039383609847 1.3213031319440816 0.6545151597367076 0.5760786099237328 1.324039473116061
X(4000) = 0.04922223042798102 1.3203298564077224 0.09243804931690679 0.9496284087750142 1.316597313359563
X(4500) = 0.4745896653599724 0.32865616721789603 0.018965010461877246 0.25384661313701296 0.18512853535354462
PC (processeur Pentium II, LINUX Mandrake 7.0, Java) :
(R+1)X-R(XX) (R+1)X-(RX)X ((R+1)-(RX))X RX+(1-(RX))X X+R(X-(XX))
X(0000) = 0.5 0.5 0.5 0.5 0.5
X(0500) = 1.2887362122471679 0.00705781307573862 1.2767485100695732 1.2465341770675666 0.03910723014701789
X(1000) = 1.3327294162589722 0.91656071198313205 1.207710752523091 0.6676224369769922 0.26663342726567785
X(1500) = 1.1448646685382955 0.44810007599150647 0.31020770014569771 0.41049165176544455 0.98416372529629426
X(2000) = 1.0548628914440754 0.89612693149716804 0.68511381901592494 1.0026346845706315 0.3860923315999224
X(2500) = 1.3328681064703032 0.06063433547953646 1.1741187260019781 0.0154001182074282 0.02087876121091203
X(3000) = 1.2956769824648844 0.0219606878364607 1.3287403237319588 0.50504896336548377 0.13270749449424302
X(3500) = 0.19193027175727995 0.37986077053509781 0.6545151597367076 0.38299434265835819 1.324039473116061
X(4000) = 1.2491385720940165 0.96017143401896088 0.09243804931690679 0.6565274346305322 1.316597313359563
X(4500) = 0.00644889182443986 1.3185465795235045 0.01896501046187725 0.94966313327336349 0.18512853535354462
Ainsi, il n'est pas surprenant de constater que là aussi
les cinq formulations donnent des résultats différents.
Par contre, il est étonnant d'observer que trois des
cinq d'entre-elles produisent, sur les deux machines,
des résultats incompatibles, les deux autres donnant des
valeurs identiques (ou presque...).
On notera pour la petite histoire qu'il est essentiel,
dans toutes ces expériences, de préciser
sans ambiguïté les versions du système et du compilateur utilisés,
au cas où ces résultats devraient être reproduits fidèlement.
Il est de plus essentiel de remarquer que d'une part, ce
calcul ne fait appel à aucune méthode numérique (d'intégration par exemple)
et que d'autre part,
ce programme ne peut être faux (ce qui peut être prouvé formellement)...
Moralité : ce programme ne calcule pas l'itération définie ci-dessus
dans le corps des nombres Réels. Oui, mais alors,
qu'étudie-t-il ? Sans que la réponse soit "n'importe quoi",
il faut bien dire que l'itération qui s'exécute effectivement
n'est pas "réellement" connue, car elle dépend d'un
trop grand nombre de paramètres non maitrisés,
voire inconnus...
Augmenter la précision des calculs (l'exemple précédent
utilise la double précision -64 bits-), ne fait
que retarder de quelque peu l'apparition du phénomène
ainsi que le montre cette expérience faite
avec bc
("arbitrary-precision arithmetic language"). Le tableau suivant
donne le numéro d'itération n
à partir duquel la partie entière est fausse,
en fonction du nombre de décimales utilisées pour
faire le calcul (paramètre scale) :
scale = 010 020 030 040 050 060 070 080 090 100
n = 035 070 105 136 169 199 230 265 303 335
Il est évident que le faible gain obtenu ne peut justifier
le coût de cette opération.
Ce qui précède ne doit pas faire croire
qu'un calcul mathématiquement linéaire soit
à l'abri de ces problèmes. Ainsi, examinons
le programme suivant
(sont mises en gras, les lignes réellement essentielles) :
main()
{
double B=4095.1;
double A=B+1;
double x=1;
int n;
printf("initialisation x = %.16f\n",x);
for (n=1 ; n <= 9 ; n++)
{
x = (A*x) - B;
printf("iteration %01d x = %+.16f\n",n,x);
}
}
Les valeurs calculées (après compilation sans optimisation par 'gcc' sur un PC Linux) sont les suivantes :
initialisation x = +1.0000000000000000
iteration 1 x = +1.0000000000004547
iteration 2 x = +1.0000000018630999
iteration 3 x = +1.0000076314440776
iteration 4 x = +1.0312591580864137
iteration 5 x = +129.0406374377594148
iteration 6 x = +524468.2550088063580915
iteration 7 x = +2148270324.2415719032287598
iteration 8 x = +8799530071030.8046875000000000
iteration 9 x = +36043755123945184.0000000000000000
Etant donné l'algorithme et, en particulier, qu'initialement :
x = 1
ainsi qu'il existe la relation suivante :
A-B = 1 (mathématiquement parlant...)
entre les constantes 'A'
(il est a noter qu'avec une partie décimale égale a 0.1, les parties entières posant
problème sont des puissances de 4 ; pour des parties décimales différentes,
la situation est plus complexe...)
et 'B',
la variable 'x' devrait être un invariant et donc rester égale a sa valeur initiale
(1) tout au long des itérations.
Or clairement,
il n'en n'est rien (et ce même apres un très petit nombre d'itérations...).
Au passage, ce programme donne la réponse attendue (1) si l'on remplace
double par float
(ce qui signifie alors tout simplement que, "par hasard",
A-B est égal exactement à 1) ou
encore si une compilation avec optimisation est demandée !
Bien sur, ce phénomène est indépendant du langage de programmation utilisé
(à condition évidemment que les compilateurs et/ou interpréteurs correspondants utilisent les nombres flottants...)
comme cela peut se voir avec les versions en C,
en Fortran 95
ou encore en Python de ce programme sans itérations (pour des raisons de simplicité).
Il conviendra donc de ne pas confondre la
linéarite mathématique et la
linéarite numérique ; cet exemple
est linéaire mathématiquement parlant mais non linéaire au
niveau du calcul numérique (une multiplication par une constante est présente,
or dans la mémoire d'un ordinateur il n'y a que peu de différences entre une
constante et une variable...) !
Au passage, ces constantes d'apparence simple ne sont pas
représentées exactement en machine :
B = 4095.1 = {0x40affe33,33333333}
A = B+1 = 4096.1 = {0x40b00019,9999999a}
A-B = 1.0000000000004547 = {0x3ff00000,00000800}
|
1.0 = {0x3ff00000,00000000}
(les valeurs précédentes ayant ete obtenues avec un PC).
Ce phénomène ne doit pas nous surprendre et est en fait
très commun : ainsi, par exemple, la
fraction 1/3 est une somme finie (un seul terme) d'inverses de puissances de 3
(1/3 s'écrit 0.1 en base 3),
alors que son écriture décimale (0.33333...) est une somme infinie
d'inverses de puissances de 10.
Notons au passage qu'évidemment (et malheureusement...) il n'existe pas de base de numération
grâce à laquelle tous les nombres auraient une représentation finie !
Les conséquences
de tout cela sont nombreuses ; en particulier,
les résultats numériques peuvent ainsi dépendre :
Ces difficultés se rencontreront a priori
avec tous les problèmes dits sensibles aux conditions initiales.
En effet, tout résultat intermédiaire dans un calcul peut être
considéré comme la condition initiale du calcul suivant. Une erreur d'arrondi
dans une valeur constitue donc une imprécision dans les conditions initiales du
calcul qui l'exploite. Mais elles pourront aussi se rencontrer avec des problèmes
linéaire comme cela fut montré précédemment...
La présence de plusieurs précisions différentes à l'intérieur d'un
même programme peut être, elle aussi,
source de difficultés importantes.
Ainsi le problème dit excess precision problem, connu
des spécialistes du compilateur 'gcc', s'est manifesté
au début de l'année 2004 dans un nouveau programme en cours de développement,
sur pratiquement tous les PCs à processeur de type x86,
sous Linux et avec compilateur 'gcc'.
Il est apparu dans celui-ci qu'un test d'ordre
strict entre deux nombres égaux 'A' et 'B' était vrai et qu'ainsi simultanément
les deux conditions 'A = B' et 'A > B' étaient vérifiées, ce phénomène
n'apparaissant que lors de compilations optimisées (à partir de '-O2').
Les tests effectués et le rôle fondamental
de l'option '-ffloat-store' (inhibant le stockage des nombres flottants
64 bits dans les registres internes 80 bits) qui fait disparaitre le phénomène
ont valide le scénario suivant :
- Soient deux nombres flottants 'A' et 'B' calculés
égaux à l'instant présent et stockés dans les registres
flottants internes 80 bits de l'unité flottante (ou 'FPU')
du processeur (de type x86). Etant tous les deux
représentés par 80 bits significatifs, ils sont "compatibles"
entre-eux ce qui signifie que l'on peut les combiner arithmétiquement
et les comparer sans ambiguité (en particulier, ils
sont présentement égaux : A = B).
- Supposons qu'un manque de ressources flottantes contraigne
le transfert du nombre 'A' en mémoire. A partir de cet instant
'A' n'est plus représenté que par 64 bits significatifs.
Imaginons alors que l'optimiseur ignore ce déplacement
(et c'est bien le cas malheureusement...).
- Supposons ensuite que quelques instructions plus tard
la comparaison de 'A' (stocké sur 64 bits en mémoire)
et de 'B' (toujours stocké sur 80 bits dans un registre) soit
demandée. Le nombre 'A' est donc retransféré dans un
registre 80 bits et donc 80-64=16 bits (nuls très certainement) lui
sont ajoutés. A partir de cet instant-là les deux
nombres 'A' et 'B' ne sont plus "compatibles"
(sauf le cas exceptionnel ou les 16 derniers bits de 'B'
sont nuls) et leur comparaison n'a plus de sens...
- Il est possible d'imaginer de nombreuses autres circonstances
où de telles difficultés apparaissent et par exemple le
cas de deux nombres 'A' et 'B' différents dans une représentation
80 bits et qui deviennent égaux en 64 bits...
Au mois de mars 2004, ce phénomène peut être observé à l'aide du programme suivant :
double f(x)
double x;
{
return(1/x);
}
main()
{
double x1=f(3.0);
volatile double x2;
x2=x1;
if (x2 != x1)
{
printf("DIFFERENT\n");
}
}
Ce programme, lorsqu'il est compilé avec 'gcc -O3 -fno-inline' sur un PC Linux
avec un processeur Intel x86, imprime le message "DIFFERENT" !
Il convient de noter qu'au mois de mars 2018, ce programme fonctionne correctement...
Il convient de noter au passage que la seule solution universelle à ce problème
(c'est-à-dire qui soit à la fois indépendante des architectures matérielles,
des constructeurs, des options de compilation,...) semble être, par
exemple dans le cas des tests, de remplacer ces derniers par des appels
à des fonctions (ceci est trivial à implémenter lors de l'utilisation
du langage K), forçant ainsi
le passage par la pile et donc par une
représentation sur 64 bits. Ainsi le test :
A > B
ou 'A' et 'B' désignent deux nombres flottants 64 bits, pourra s'écrire :
fIFGT(A,B)
la fonction 'fIFGT(...)' étant définie par :
unsigned int fIFGT(x,y)
double x;
double y;
{
return(x > y);
}
et en faisant en sorte qu'elle ne puisse être développée (inlined)
par le compilateur (option '-fno-inline' de 'gcc')...
Ainsi, augmenter la précision et/ou utiliser simultanément plusieurs
précisions différentes peut entrainer des difficultés et des complications imprevues...
Le passage par des fonctions pour exécuter les instructions élémentaires
(addition, soustraction, multiplication, division, tests,...)
d'un programme, même s'il est parfois pénalisant au niveau des
performances, possède un autre avantage :
il permet d'imposer l'ordre d'exécution de celles-ci,
alors qu'ainsi que cela fut montre précédemment, celui-ci peut influer
de façon plus ou moins importante, voire dramatique,
sur les résultats obtenus.
En effet, en toute généralité :
F.G # G.F
'F' et 'G' désignant deux fonctions arbitraires ; les compilateurs
n'ont donc absolument pas le droit de remplacer 'F(G(...))' par 'G(F(...))'.
Ainsi, par exemple,
ces deux images 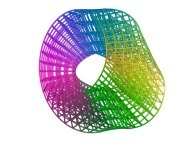 et
et 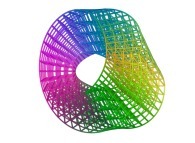 ,
calculées à l'aide d'un processus non itératif
sur la même machine (un PC sous Linux), avec et sans imposer l'ordre respectivement,
semblent identiques,
alors qu'elles sont en réalité légèrement différentes.
Au passage, l'utilisation de fonctions présente un autre avantage :
celui de permettre l'extension de l'arithmétique.
,
calculées à l'aide d'un processus non itératif
sur la même machine (un PC sous Linux), avec et sans imposer l'ordre respectivement,
semblent identiques,
alors qu'elles sont en réalité légèrement différentes.
Au passage, l'utilisation de fonctions présente un autre avantage :
celui de permettre l'extension de l'arithmétique.
Ainsi, ces problèmes peuvent se manifester même en dehors des systèmes
itératifs. Dans ces derniers les erreurs d'arrondis se trouvent amplifiées
numériquement lors des calculs successifs, alors que dans les cas illustrés par
l'exemple précédent, l'amplification peut être d'une autre nature.
Ici, elle peut être qualifiée de "visuelle" et s'analyse de la façon
suivante : imaginons deux points P1(x1,y1,z1) et P2(x2,y2,z2) mathématiquement identiques
(x1=x2, y1=y2 et z1=z2) et ne différant que par leur couleur (rouge pour P1 et vert
pour P2). Supposons l'axe 'OZ' orthogonal au plan de l'image et orienté vers l'observateur.
Puis imaginons que la compilation
du programme ait lieu sur deux machines identiques, à la version de leur compilateur près.
Nous pourrons obtenir (et c'est le phénomène rencontré dans l'exemple précédent !)
{x1=x2, y1=y2 et z1>z2} sur la première (d'ou un point rouge -P1 est devant P2-)
et {x2=x1, y2=y1 et z2>z1} sur la seconde (d'ou un point vert -P2 est devant P1-)...
Enfin, utiliser l'arithmétique dite
d'intervalle, semble
aussi voué à l'échec sur les problèmes sensibles aux conditions initiales
(comme l'est l'exemple précédent). En effet, un intervalle
[x-epsilon,x+epsilon] encadrant une valeur exacte ne peut,
en toute généralité, qu'"exploser" au cours
des calculs suivants,
puisque 'x-epsilon' et 'x+epsilon' peuvent être considérées
comme deux conditions initiales très voisines l'une de l'autre...
Le problème des N-corps donne
un exemple concret de ces difficultés.
Alors, ne pourrait-on pas se passer des Nombres Réels pour faire de la physique mathématique ?
Copyright © Jean-François COLONNA, 2004-2026.
Copyright © France Telecom R&D and CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2004-2026.

 et
et  ,
calculées à l'aide d'un processus non itératif
sur la même machine (un PC sous Linux), avec et sans imposer l'ordre respectivement,
semblent identiques,
alors qu'elles sont en réalité légèrement différentes.
Au passage, l'utilisation de fonctions présente un autre avantage :
celui de permettre l'extension de l'arithmétique.
,
calculées à l'aide d'un processus non itératif
sur la même machine (un PC sous Linux), avec et sans imposer l'ordre respectivement,
semblent identiques,
alors qu'elles sont en réalité légèrement différentes.
Au passage, l'utilisation de fonctions présente un autre avantage :
celui de permettre l'extension de l'arithmétique.