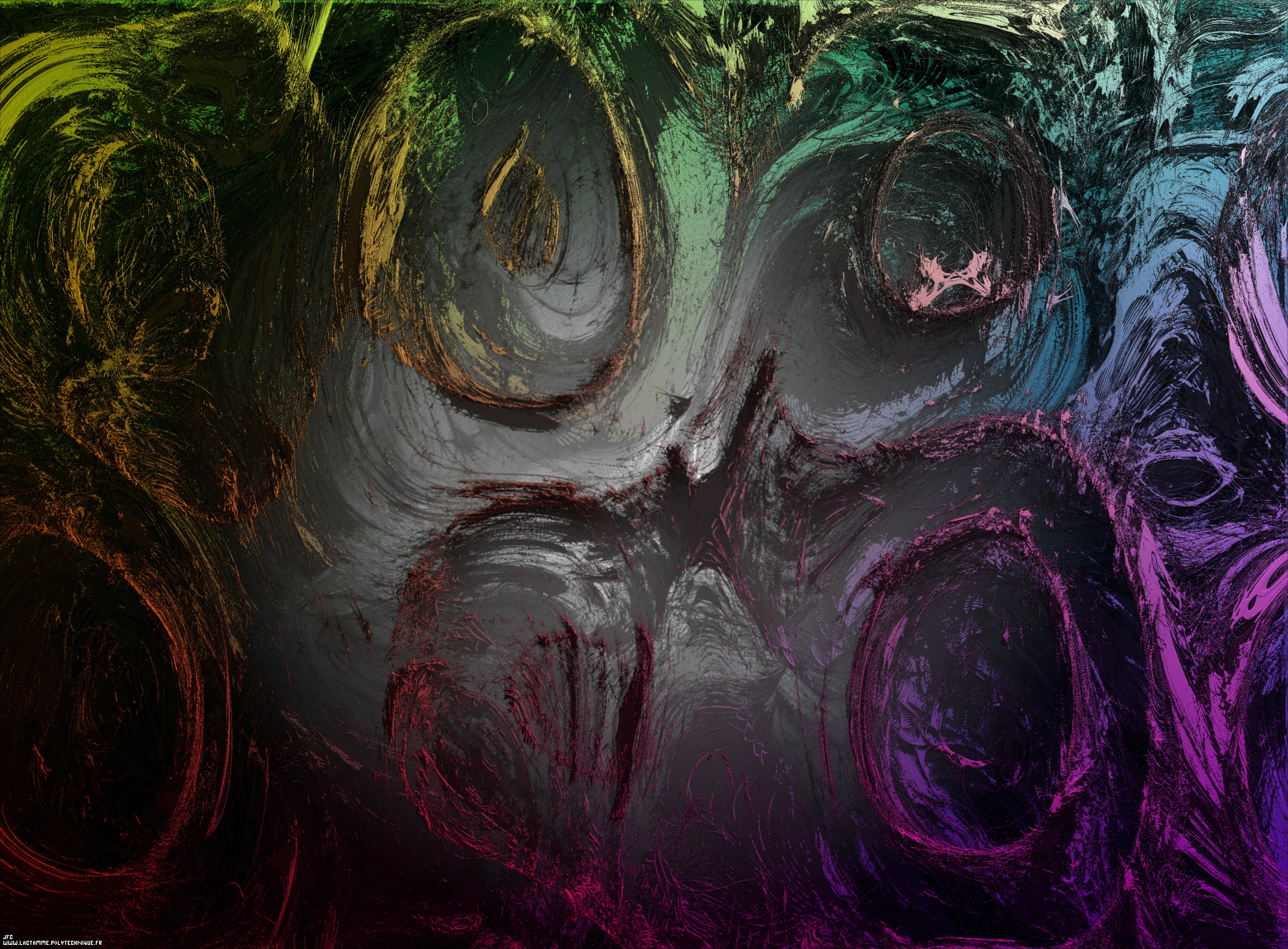
Tridimensional visualization of the Verhulst dynamics with a tridimensional non linear transformation of the coordinates [Visualisation tridimensionnelle de la dynamique de Verhulst avec une transformation non linéaire tridimensionnelle des coordonnées].
The Verhulst dynamics is defined using the following iteration:
X = 0.5
0
X = RX (1 - X )
n n-1 n-1
Here, in this computation, the growing rate 'R' is no longer constant but changes its value periodically
using the following arbitrary cycle:
R3 ==> R3 ==> R3 ==> R3 ==> R2 ==> R2 ==> R2 ==> R1 ==> R1 ==> R1 ==> R1 ==> R2 ==> R2 ==> R3 ==> R3 ==> R2 ==> R1 ==> R1 ==> R1 ==> R1 ==> R2 ==> R2 ==> R3 ==> R3 ==> R2 ==> R2 ==> R1 ==> R1 ==> R1 ==> R1 ==> R1 ==> R1
where {R1,R2,R3} are respectively the three coordinates of the current point
inside the following domain [2.936,3.413]x[3.500,3.850]x[3.000,4.000].
Only the points corresponding to a dynamical system with a negative Lyapunov exponent are displayed.
This process gives birth to the following tridimensionnal structure:

Then a tridimensional non linear transformation of the coordinates is applied.
It is defined using the pseudo-projection
of an interpolation between the Bonan-Jeener's triple Klein bottle
and a "double sphere":
{tX=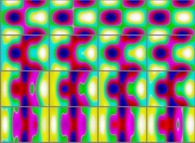 ,tY=
,tY= ,tZ=
,tZ=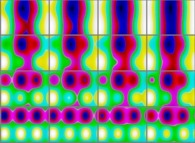 } ==>
} ==> 
See some related pictures (possibly including this one):











































See a bidimensionnal dynamics:

(CMAP28 WWW site: this page was created on 10/21/2015 and last updated on 10/11/2024 21:07:14 -CEST-)
[See all related pictures (including this one) [Voir toutes les images associées (incluant celle-ci)]]
[See the following comment(s): Verhulst dynamics [Voir le(s) commentaire(s) suivant(s): dynamique de Verhulst]]
[Please visit the related ArtAndScience picture gallery [Visitez la galerie d'images ArtAndScience associée]]
[Go back to AVirtualMachineForExploringSpaceTimeAndBeyond [Retour à AVirtualMachineForExploringSpaceTimeAndBeyond]]
[The Y2K Bug [Le bug de l'an 2000]]
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[Mail [Courrier]]
[About Pictures and Animations [A Propos des Images et des Animations]]
Copyright © Jean-François COLONNA, 2015-2024.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2015-2024.
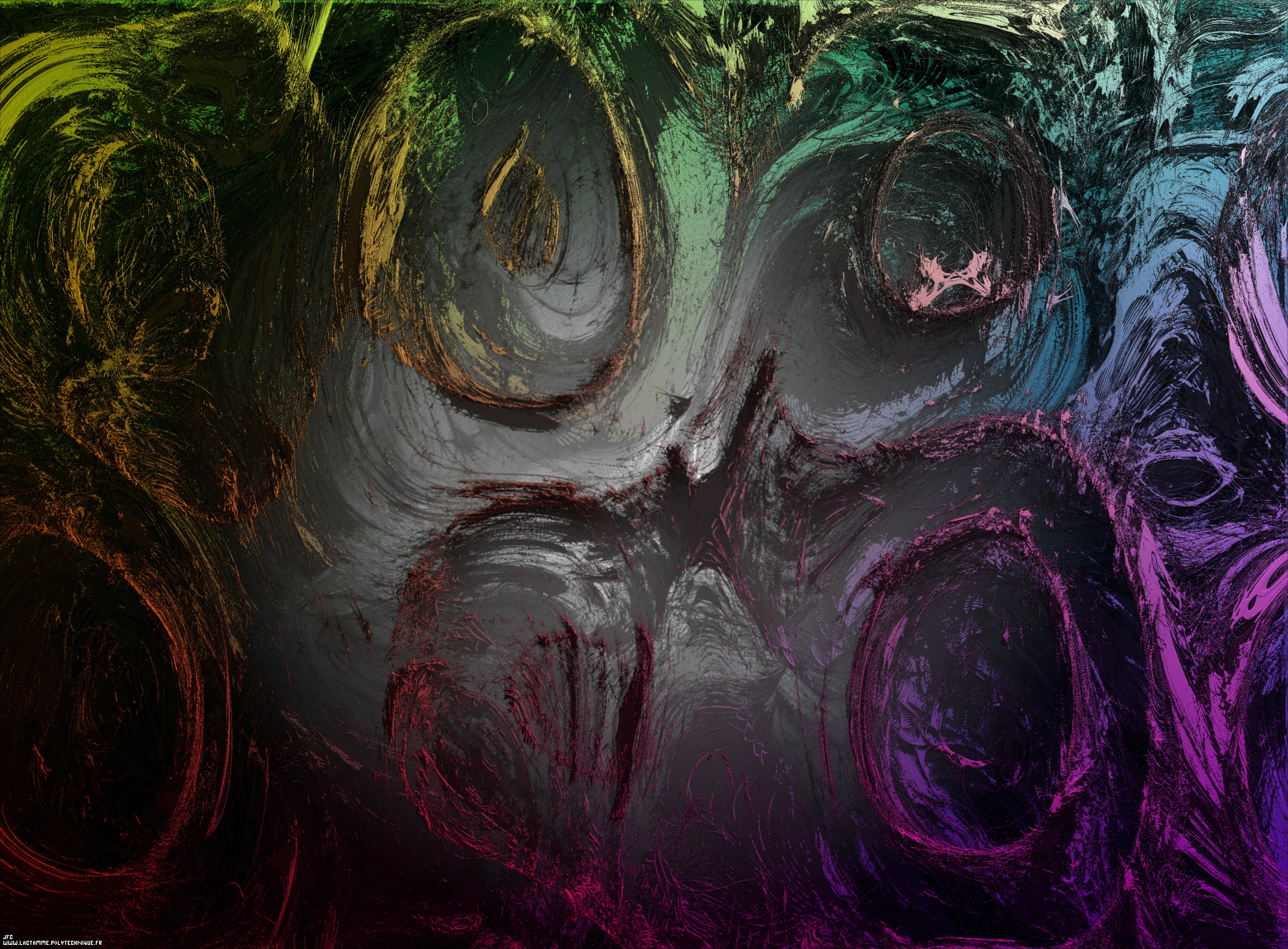

 ,tY=
,tY= ,tZ=
,tZ= } ==>
} ==> 

































