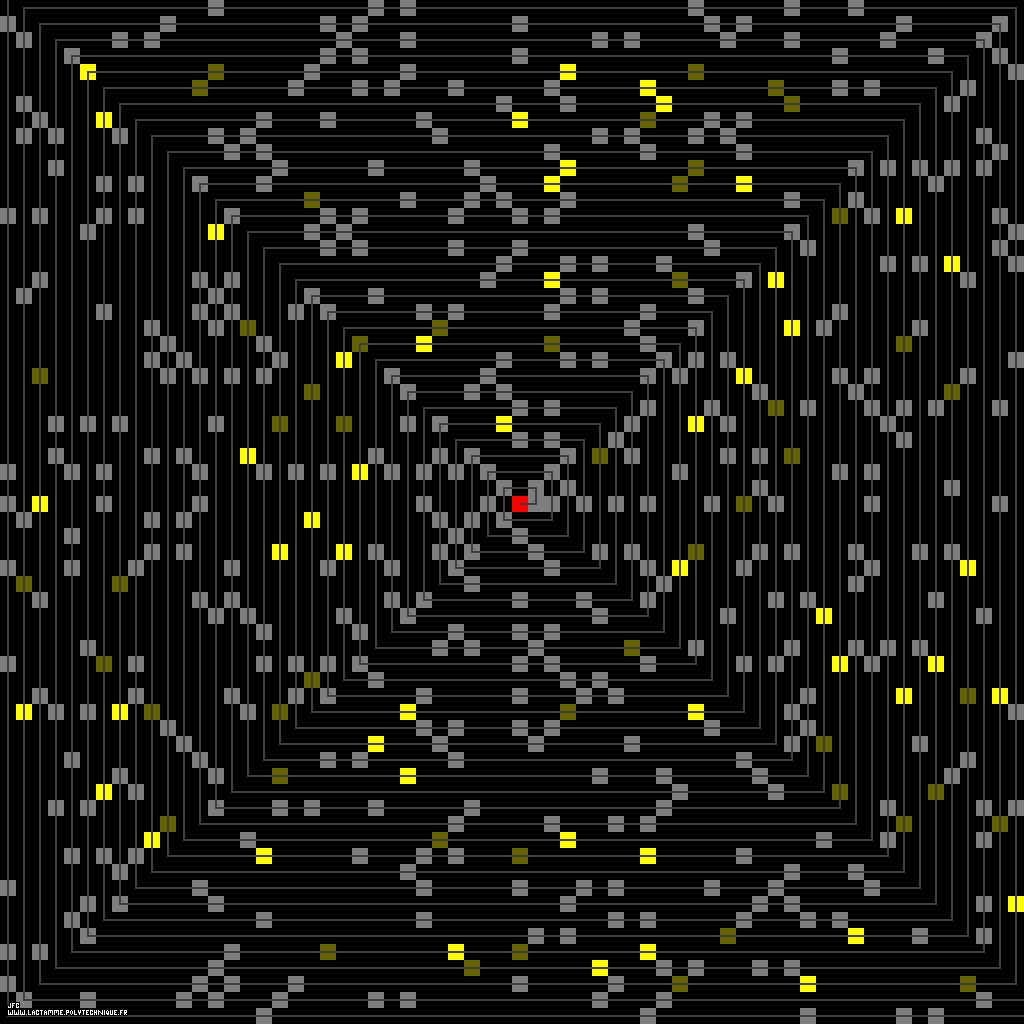
The Ulam spiral with display of the first '8-twin' prime numbers [La spirale d'Ulam montrant les premiers nombres premiers '8-jumeaux'].




Starting from the center of the picture -red square-, all the little squares (even the black ones) are numbered (N=1, 2, 3,...) when following a square spiral. A '8-twin' prime number pair is a set of two prime numbers {P1,P2} such that on the one hand P2-P1=8 and on the other hand there are no prime number between P1 and P2. The yellow squares display the first '8-twin' prime number pairs (light yellow for P2 and dark yellow for P1).

A famous conjecture states that there are infinitely many '2-twin' prime number pairs {2,3,5,7,11,13,17,19,23,29,31,37,41,... (INFINITY?)}.


See the Ulam spiral:




See the 'N-twin' prime numbers (with N=2,4,6,8 respectively):




See the generalized Ulam spiral:




[Plus d'informations à propos de la spirale d'Ulam et de ses généralisations -en français/in french-]
[More information about the Ulam spiral and ist generalizations -in english/en anglais-]


(CMAP28 WWW site: this page was created on 04/01/2015 and last updated on 08/22/2020 11:13:50 -CEST-)



[See all related pictures (including this one) [Voir toutes les images associées (incluant celle-ci)]]

[Please visit the related NumberTheory picture gallery [Visitez la galerie d'images NumberTheory associée]]
[Go back to AVirtualMachineForExploringSpaceTimeAndBeyond [Retour à AVirtualMachineForExploringSpaceTimeAndBeyond]]
[The Y2K bug [Le bug de l'an 2000]]

[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[Mail [Courrier]]
[About Pictures and Animations [A Propos des Images et des Animations]]


Copyright (c) Jean-François Colonna, 2015-2020.
Copyright (c) CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / Ecole Polytechnique, 2015-2020.