Jean-François COLONNA
[Contact me]
www.lactamme.polytechnique.fr
CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[Real Numbers don't exist in Computers and Floating Point Computations aren't safe. [Les Nombres Réels n'existent pas dans les Ordinateurs et les Calculs Flottants ne sont pas sûrs.]]
[N'oubliez pas de visiter Une Machine Virtuelle à Explorer l'Espace-Temps et au-delà où vous trouverez plus de 10.000 images et animations à la frontière de l'Art et de la Science]
(Site WWW CMAP28 : cette page a été créée le 21/11/2013 et mise à jour le 03/10/2024 17:09:09 -CEST-)
 :
La surface de la Lune modélisée grâce à la géométrie fractale. Un monticule "non naturel"
(construit à partir du visage de Flore dans le Printemps de Botticelli...) situé au milieu et à droite
a été introduit a posteriori afin de "signer" la nature mathématique de ce paysage.
:
La surface de la Lune modélisée grâce à la géométrie fractale. Un monticule "non naturel"
(construit à partir du visage de Flore dans le Printemps de Botticelli...) situé au milieu et à droite
a été introduit a posteriori afin de "signer" la nature mathématique de ce paysage.
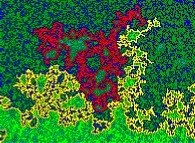 :
La diffusion bidimensionnelle. Des particules sont injectées en bas d'un espace initialement vide -bleu- et s'y déplacent
ensuite par une marche aléatoire. Au bout d'un certain temps, les particules ont envahi une bonne partie du milieu et
le front dit de diffusion -jaune- est une courbe fractale. Bernard Sapoval et ses collaborateurs avaient conjecturé dans
les années quatre-vingt que sa dimension était égale à 7/4. Cette étonnante propriété a été
demontrée quelques années plus tard, en particulier par Wendelin Werner (Médaille Fields 2006). Une découverte importante a
été faite grâce à une image de ce type : l'unique particule marquée en blanc, si elle vient à occuper
le site libre situé immédiatement à sa droite provoque alors le rattachement de l'agrégat de particules rouges au
front de diffusion. Ainsi, un événement microscopique peut avoir instantanément des conséquences macroscopiques.
:
La diffusion bidimensionnelle. Des particules sont injectées en bas d'un espace initialement vide -bleu- et s'y déplacent
ensuite par une marche aléatoire. Au bout d'un certain temps, les particules ont envahi une bonne partie du milieu et
le front dit de diffusion -jaune- est une courbe fractale. Bernard Sapoval et ses collaborateurs avaient conjecturé dans
les années quatre-vingt que sa dimension était égale à 7/4. Cette étonnante propriété a été
demontrée quelques années plus tard, en particulier par Wendelin Werner (Médaille Fields 2006). Une découverte importante a
été faite grâce à une image de ce type : l'unique particule marquée en blanc, si elle vient à occuper
le site libre situé immédiatement à sa droite provoque alors le rattachement de l'agrégat de particules rouges au
front de diffusion. Ainsi, un événement microscopique peut avoir instantanément des conséquences macroscopiques.
 :
Une seule et même matrice visualisée avec quatre conventions de coloriage différentes !
:
Une seule et même matrice visualisée avec quatre conventions de coloriage différentes !
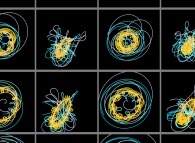 :
Le système solaire vu depuis seize planètes virtuelles de trajectoires très différentes
(de plus grandes excentricités et situées en dehors du plan de l'écliptique) de celle de la Terre.
Le mouvement apparent des planètes réelles et du Soleil est beaucoup plus complexe que celui que nous
montrent les épicycles de Ptolémée et semble presque chaotique, alors que les mouvements réels
restent quasiment-elliptiques... Alors quelles sciences, quelles philosophies ou encore quelles religions
sur ces planètes ?
:
Le système solaire vu depuis seize planètes virtuelles de trajectoires très différentes
(de plus grandes excentricités et situées en dehors du plan de l'écliptique) de celle de la Terre.
Le mouvement apparent des planètes réelles et du Soleil est beaucoup plus complexe que celui que nous
montrent les épicycles de Ptolémée et semble presque chaotique, alors que les mouvements réels
restent quasiment-elliptiques... Alors quelles sciences, quelles philosophies ou encore quelles religions
sur ces planètes ?
 :
Variétés de Calabi-Yau (échelle de Planck). Dans le cadre de la théorie des super-cordes,
notre espace pourrait avoir dix dimensions au lieu des trois qui nous sont familières (représentées par
le réseau cubique blanc).
:
Variétés de Calabi-Yau (échelle de Planck). Dans le cadre de la théorie des super-cordes,
notre espace pourrait avoir dix dimensions au lieu des trois qui nous sont familières (représentées par
le réseau cubique blanc).

 :
L'art potentiel (à gauche une sculpture fractale et à droite un hommage à Yves Tanguy).
:
L'art potentiel (à gauche une sculpture fractale et à droite un hommage à Yves Tanguy).