Intéressons-nous à quelques conséquences malheureuses de cela lors de calculs
utilisant les nombres flottants.
Les nombres flottants ne sont pas des nombres au sens mathématique du terme car, en effet,
en ce qui concerne l'addition et la multiplication,
les propriété d'associativité et de distributivité sont perdues. Rappelons que ces
propriétés signifient respectivement :
(AxB)xC = Ax(BxC)
(A+B)+C = A+(B+C)
Ax(B+C) = AxB+AxC
pour tout triplet de nombres 'A', 'B' et 'C'. Vérifions-le pour l'associativité en
essayant les deux petits programmes suivant écrits
dans le langage C (ces programmes sont communiqués au lecteur afin de permettre à tout un chacun
de reproduire le phénomène) :
double addition(x,y) double multiplication(x,y)
double x; double x;
double y; double y;
{ {
return(x+y); return(x*y);
} }
main() main()
{ {
double a=1.1; double a=1.5;
double b=3.7; double b=2.3;
double c=5.5; double c=3.7;
double x1,x2; double x1,x2;
x1 = addition(addition(a,b),c); x1 = multiplication(multiplication(a,b),c);
x2 = addition(a,addition(b,c)); x2 = multiplication(a,multiplication(b,c));
printf("(%.6f + %.6f) + %.6f = %.15f\n",a,b,c,x1); printf("(%.6f * %.6f) * %.6f = %.15f\n",a,b,c,x1);
printf("%.6f + (%.6f + %.6f) = %.15f\n",a,b,c,x2); printf("%.6f * (%.6f * %.6f) = %.15f\n",a,b,c,x2);
} }
(1.100000 + 3.700000) + 5.500000 = 10.300000000000001 (1.500000 * 2.300000) * 3.700000 = 12.764999999999999
1.100000 + (3.700000 + 5.500000) = 10.299999999999999 1.500000 * (2.300000 * 3.700000) = 12.765000000000001
On notera l'utilisation de deux fonctions destinées à effectuer l'addition et la multiplication
respectivement ; elles sont là afin de faire respecter impérativement l'ordre des opérations
(en effet, pour un compilateur les deux expressions (A+B)+C et A+(B+C) à sont équivalentes,
les parenthèses étant redondantes ; il en est de même pour (AxB)xC et Ax(BxC)).
Les résultats obtenus sont différents mais malgré tout proches l'un de l'autre. Mais en est-il
toujours ainsi ? Exploitons cet autre petit programme (pour des raisons de simplicité et de
compréhension la notion d'itération
n'y est pas utilisée) :
main()
{
double A,B,x0,x1,x2,x3,x4,x5,x6,x7;
B=4095.1;
A=B+1;
x0 = 1;
x1 = (A*x0) - B;
x2 = (A*x1) - B;
x3 = (A*x2) - B;
x4 = (A*x3) - B;
x5 = (A*x4) - B;
x6 = (A*x5) - B;
x7 = (A*x6) - B;
printf("x0 = %+.16f\n",x0);
printf("x1 = %+.16f\n",x1);
printf("x2 = %+.16f\n",x2);
printf("x3 = %+.16f\n",x3);
printf("x4 = %+.16f\n",x4);
printf("x5 = %+.16f\n",x5);
printf("x6 = %+.16f\n",x6);
printf("x7 = %+.16f\n",x7);
}
x0 = +1.0000000000000000
x1 = +1.0000000000004547
x2 = +1.0000000018630999
x3 = +1.0000076314440776
x4 = +1.0312591580864137
x5 = +129.0406374377594148
x6 = +524468.2550088063580915
x7 = +2148270324.2415719032287598
On notera au préalable que ce programme très simple ne contient pas d'erreur de conception
(ne peut pas contenir...),
ne fait pas appel à des méthodes d'approximation
(contrairement au dernier exemple)
et qu'enfin les réponses attendues (=1)
sont connues a priori (ce qui est exceptionnel !).
En effet, la propriété suivante est vraie :
A=B+1 ==> A-B=1 ==> x7=x6=x5=x4=x3=x2=x1=x0=1
Mais ce programme ne donne pas du tout des valeurs égales à 1 (sauf évidemment la première).
Où est le problème ?
En fait, A-B n'est pas égale à 1 ; A-B est égale à 1
plus/moins epsilon (un simple bit), tout simplement parce que 4095.1 et 4096.1
ne sont pas représentables exactement dans un ordinateur à l'aide des
nombres flottants !
Il est évidemment possible d'imaginer d'autres façons de faire qui résoudraient ce
problème : par exemple en représentant 4095.1 et 4096.1 à l'aide des deux
fractions 40951/10 et 40961/10 et en ne travaillant ainsi qu'avec des nombres entiers.
Ou bien encore concevoir que le compilateur, par des manipulations "formelles",
pourrait se rendre compte que tous les x[i] sont égaux à 1 et remplacer alors
les instructions 'x[i+1]=(A*x[i])-B' par 'x[i+1]=1'. Mais cela ne ferait que répondre à
ce cas particulier sans résoudre le problème général qui vient encore une
fois de la capacité finie des ordinateurs...
Evidemment ce phénomène est indépendant du langage de programmation utilisé
comme cela peut se voir avec les versions
en Fortran 95
ou encore en Python de ce programme.
L'intérêt de ce programme est donc d'une part de révéler de façon tout à fait
violente un problème général d'exactitude des calculs dans un ordinateur.
D'autre part il montre qu'une erreur infime (le simple bit qui faisait que A-B n'était
pas égal à 1) peut s'amplifier de manière "explosive" !
Enfin, il fait
référence à un processus appelé calcul itératif
omniprésent, en particulier, en physique mathématique où une grandeur
est transformée et retransformé suivant certaines lois. Cela sera le cas dans le
dernier exemple avec les coordonnées tridimensionnelles des
quatre corps (deux étoiles et deux planètes). En effet, ces dernières seront données
a priori à l'instant initial puis transformées ensuite d'instants
en instants selon les lois de Newton de la Physique classique.
Enfin, on notera qu'un problème linéaire mathématiquement peut ne plus l'être informatiquement
(l'ordinateur ne faisant pas la différence entre une constante et une variable) !

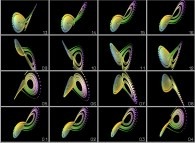 faire coopérer des ordinateurs différents
faire coopérer des ordinateurs différents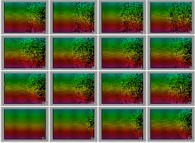 l'irréversibilité du temps numérique
l'irréversibilité du temps numérique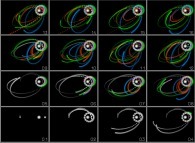 Cette expérience
Cette expérience