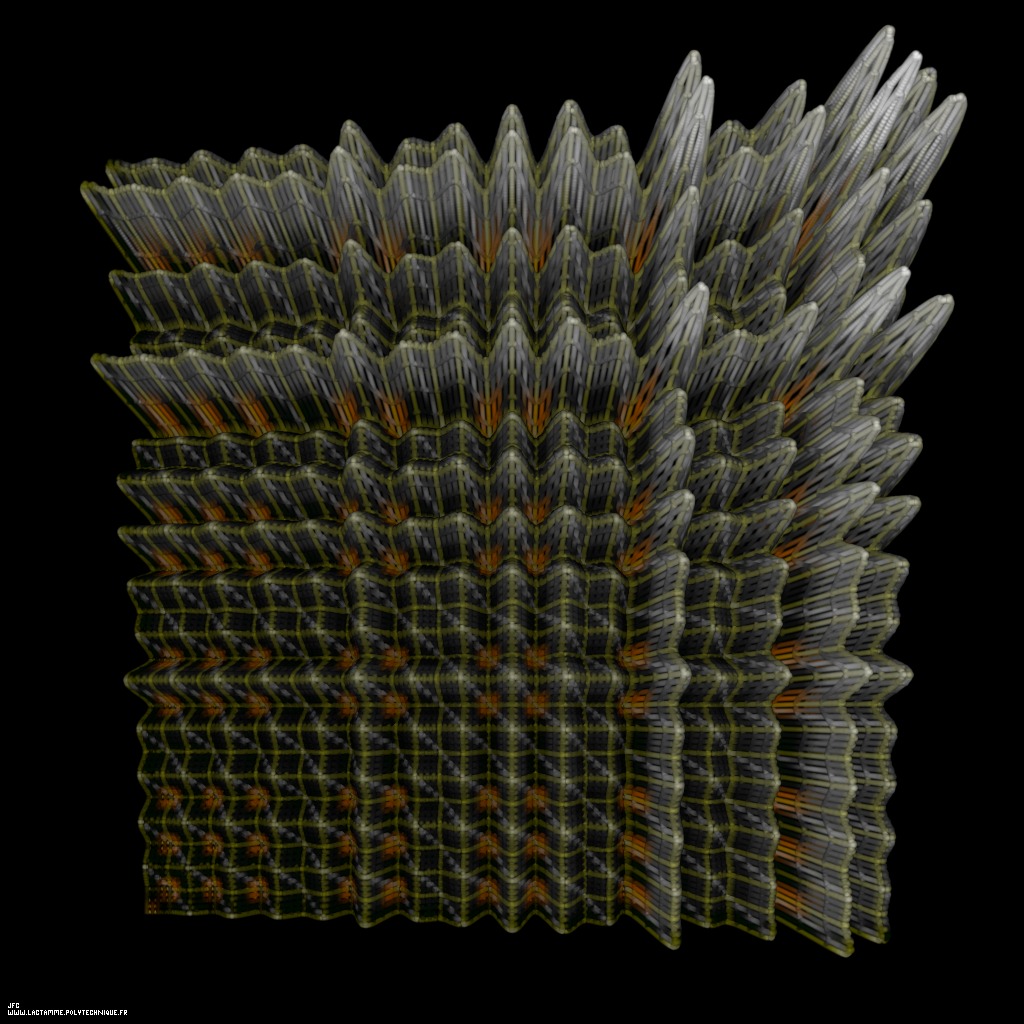
Tridimenional display of the Goldbach Conjecture [Visualisation tridimensionnelle de la conjecture de Goldbach].

Tridimenional display of the Goldbach Conjecture [Visualisation tridimensionnelle de la conjecture de Goldbach].
4 = 2+2
6 = 3+3
8 = 3+5 [= 5+3]
10 = 3+7 = 5+5 [= 7+3]
(...)
990 = 7+983 = 13+977 = 19+971 = 23+967 = 37+953 = 43+947 = 53+937 = 61+929 = 71+919 = 79+911
= 83+907 = 103+887 = 107+883 = 109+881 = 113+877 = 127+863 = 131+859 = 137+853 = 151+839 = 163+827
= 167+823 = 179+811 = 181+809 = 193+797 = 229+761 = 233+757 = 239+751 = 251+739 = 257+733 = 263+727
= 271+719 = 281+709 = 307+683 = 313+677 = 317+673 = 331+659 = 337+653 = 347+643 = 349+641 = 359+631
= 373+617 = 383+607 = 389+601 = 397+593 = 419+571 = 421+569 = 433+557 = 443+547 = 449+541 = 467+523
= 487+503 = 491+499
[= 499+491 = 503+487 = 523+467 = 541+449 = 547+443 = 557+433 = 569+421 = 571+419 = 593+397 = 601+389
= 607+383 = 617+373 = 631+359 = 641+349 = 643+347 = 653+337 = 659+331 = 673+317 = 677+313 = 683+307
= 709+281 = 719+271 = 727+263 = 733+257 = 739+251 = 751+239 = 757+233 = 761+229 = 797+193 = 809+181
= 811+179 = 823+167 = 827+163 = 839+151 = 853+137 = 859+131 = 863+127 = 877+113 = 881+109 = 883+107
= 887+103 = 907+83 = 911+79 = 919+71 = 929+61 = 937+53 = 947+43 = 953+37 = 967+23 = 971+19
= 977+13 = 983+7]
(...)
Each straight line (with equation y=-x+N) of this picture displays an even integer number N
and each orange square with center coordinates {x=P1,y=P2} exhibits a couple of prime numbers P1 and P2
such that:
N = P1+P2In order to exhibit the commutativity of the addition, both {P1,P2} and {P2,P1} couples are displayed, hence the symmetry.
SD(2) = 1+2 = 3
SD(3) = 1+3 = 4
SD(4) = 1+2+4 = 7
SD(5) = 1+5 = 6
SD(6) = 1+2+3+6 = 12
SD(7) = 1+7 = 8
(...)
When N is a Prime Number P:
SD(P) = 1+PThis picture displays the surface {x,y,(SD(x)+SD(y))-(x+y+2)} and the luminance of each point is proportional to its third coordinate. For each even integer number N, the lowest points of the x+y=N straight line (white) correspond to couple {P1,P2} of Prime Numbers (orange squares). There is always at least one such orange square on each white line: this is the Goldbach conjecture. By the way:
SD(P1) = 1+P1
SD(P2) = 1+P2
SD(P1)+SD(P2) = (1+P1)+(1+P2)
SD(P1)+SD(P2) = P1+P2+2
SD(P1)+SD(P2) = N+2
hence:
(SD(P1)+SD(P2))-(N+2) = 0


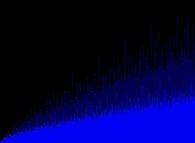
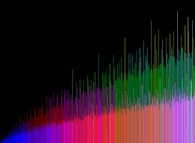




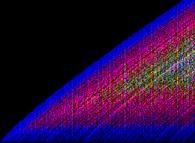



4 = 2+2 (# 1) 6 = 3+3 (# 1) 8 = 3+5 = 5+3 (# 2) 10 = 3+7 = 5+5 = 7+3 (# 3) 12 = 5+7 = 7+5 (# 2) 14 = 3+11 = 7+7 = 11+3 (# 3) 16 = 3+13 = 5+11 = 11+5 = 13+3 (# 4) 18 = 5+13 = 7+11 = 11+7 = 13+5 (# 4) 20 = 3+17 = 7+13 = 13+7 = 17+3 (# 4) 22 = 3+19 = 5+17 = 11+11 = 17+5 = 19+3 (# 5) 24 = 5+19 = 7+17 = 11+13 = 13+11 = 17+7 = 19+5 (# 6) 26 = 3+23 = 7+19 = 13+13 = 19+7 = 23+3 (# 5) 28 = 5+23 = 11+17 = 17+11 = 23+5 (# 4) 30 = 7+23 = 11+19 = 13+17 = 17+13 = 19+11 = 23+7 (# 6) 32 = 3+29 = 13+19 = 19+13 = 29+3 (# 4) 34 = 3+31 = 5+29 = 11+23 = 17+17 = 23+11 = 29+5 = 31+3 (# 7) 36 = 5+31 = 7+29 = 13+23 = 17+19 = 19+17 = 23+13 = 29+7 = 31+5 (# 8) 38 = 7+31 = 19+19 = 31+7 (# 3) 40 = 3+37 = 11+29 = 17+23 = 23+17 = 29+11 = 37+3 (# 6) 42 = 5+37 = 11+31 = 13+29 = 19+23 = 23+19 = 29+13 = 31+11 = 37+5 (# 8) 44 = 3+41 = 7+37 = 13+31 = 31+13 = 37+7 = 41+3 (# 6) 46 = 3+43 = 5+41 = 17+29 = 23+23 = 29+17 = 41+5 = 43+3 (# 7) 48 = 5+43 = 7+41 = 11+37 = 17+31 = 19+29 = 29+19 = 31+17 = 37+11 = 41+7 = 43+5 (# 10) 50 = 3+47 = 7+43 = 13+37 = 19+31 = 31+19 = 37+13 = 43+7 = 47+3 (# 8) 52 = 5+47 = 11+41 = 23+29 = 29+23 = 41+11 = 47+5 (# 6) 54 = 7+47 = 11+43 = 13+41 = 17+37 = 23+31 = 31+23 = 37+17 = 41+13 = 43+11 = 47+7 (# 10) 56 = 3+53 = 13+43 = 19+37 = 37+19 = 43+13 = 53+3 (# 6) 58 = 5+53 = 11+47 = 17+41 = 29+29 = 41+17 = 47+11 = 53+5 (# 7) 60 = 7+53 = 13+47 = 17+43 = 19+41 = 23+37 = 29+31 = 31+29 = 37+23 = 41+19 = 43+17 = 47+13 = 53+7 (# 12) 62 = 3+59 = 19+43 = 31+31 = 43+19 = 59+3 (# 5) 64 = 3+61 = 5+59 = 11+53 = 17+47 = 23+41 = 41+23 = 47+17 = 53+11 = 59+5 = 61+3 (# 10) 66 = 5+61 = 7+59 = 13+53 = 19+47 = 23+43 = 29+37 = 37+29 = 43+23 = 47+19 = 53+13 = 59+7 = 61+5 (# 12) 68 = 7+61 = 31+37 = 37+31 = 61+7 (# 4) 70 = 3+67 = 11+59 = 17+53 = 23+47 = 29+41 = 41+29 = 47+23 = 53+17 = 59+11 = 67+3 (# 10) 72 = 5+67 = 11+61 = 13+59 = 19+53 = 29+43 = 31+41 = 41+31 = 43+29 = 53+19 = 59+13 = 61+11 = 67+5 (# 12) 74 = 3+71 = 7+67 = 13+61 = 31+43 = 37+37 = 43+31 = 61+13 = 67+7 = 71+3 (# 9) 76 = 3+73 = 5+71 = 17+59 = 23+53 = 29+47 = 47+29 = 53+23 = 59+17 = 71+5 = 73+3 (# 10) 78 = 5+73 = 7+71 = 11+67 = 17+61 = 19+59 = 31+47 = 37+41 = 41+37 = 47+31 = 59+19 = 61+17 = 67+11 = 71+7 = 73+5 (# 14) 80 = 7+73 = 13+67 = 19+61 = 37+43 = 43+37 = 61+19 = 67+13 = 73+7 (# 8) 82 = 3+79 = 11+71 = 23+59 = 29+53 = 41+41 = 53+29 = 59+23 = 71+11 = 79+3 (# 9) 84 = 5+79 = 11+73 = 13+71 = 17+67 = 23+61 = 31+53 = 37+47 = 41+43 = 43+41 = 47+37 = 53+31 = 61+23 = 67+17 = 71+13 = 73+11 = 79+5 (# 16) 86 = 3+83 = 7+79 = 13+73 = 19+67 = 43+43 = 67+19 = 73+13 = 79+7 = 83+3 (# 9) 88 = 5+83 = 17+71 = 29+59 = 41+47 = 47+41 = 59+29 = 71+17 = 83+5 (# 8) 90 = 7+83 = 11+79 = 17+73 = 19+71 = 23+67 = 29+61 = 31+59 = 37+53 = 43+47 = 47+43 = 53+37 = 59+31 = 61+29 = 67+23 = 71+19 = 73+17 = 79+11 = 83+7 (# 18) 92 = 3+89 = 13+79 = 19+73 = 31+61 = 61+31 = 73+19 = 79+13 = 89+3 (# 8) 94 = 5+89 = 11+83 = 23+71 = 41+53 = 47+47 = 53+41 = 71+23 = 83+11 = 89+5 (# 9) 96 = 7+89 = 13+83 = 17+79 = 23+73 = 29+67 = 37+59 = 43+53 = 53+43 = 59+37 = 67+29 = 73+23 = 79+17 = 83+13 = 89+7 (# 14) 98 = 19+79 = 31+67 = 37+61 = 61+37 = 67+31 = 79+19 (# 6) 100 = 3+97 = 11+89 = 17+83 = 29+71 = 41+59 = 47+53 = 53+47 = 59+41 = 71+29 = 83+17 = 89+11 = 97+3 (# 12) 102 = 5+97 = 13+89 = 19+83 = 23+79 = 29+73 = 31+71 = 41+61 = 43+59 = 59+43 = 61+41 = 71+31 = 73+29 = 79+23 = 83+19 = 89+13 = 97+5 (# 16) 104 = 3+101 = 7+97 = 31+73 = 37+67 = 43+61 = 61+43 = 67+37 = 73+31 = 97+7 = 101+3 (# 10) 106 = 3+103 = 5+101 = 17+89 = 23+83 = 47+59 = 53+53 = 59+47 = 83+23 = 89+17 = 101+5 = 103+3 (# 11) 108 = 5+103 = 7+101 = 11+97 = 19+89 = 29+79 = 37+71 = 41+67 = 47+61 = 61+47 = 67+41 = 71+37 = 79+29 = 89+19 = 97+11 = 101+7 = 103+5 (# 16) 110 = 3+107 = 7+103 = 13+97 = 31+79 = 37+73 = 43+67 = 67+43 = 73+37 = 79+31 = 97+13 = 103+7 = 107+3 (# 12) 112 = 3+109 = 5+107 = 11+101 = 23+89 = 29+83 = 41+71 = 53+59 = 59+53 = 71+41 = 83+29 = 89+23 = 101+11 = 107+5 = 109+3 (# 14) 114 = 5+109 = 7+107 = 11+103 = 13+101 = 17+97 = 31+83 = 41+73 = 43+71 = 47+67 = 53+61 = 61+53 = 67+47 = 71+43 = 73+41 = 83+31 = 97+17 = 101+13 = 103+11 = 107+7 = 109+5 (# 20) 116 = 3+113 = 7+109 = 13+103 = 19+97 = 37+79 = 43+73 = 73+43 = 79+37 = 97+19 = 103+13 = 109+7 = 113+3 (# 12) 118 = 5+113 = 11+107 = 17+101 = 29+89 = 47+71 = 59+59 = 71+47 = 89+29 = 101+17 = 107+11 = 113+5 (# 11) 120 = 7+113 = 11+109 = 13+107 = 17+103 = 19+101 = 23+97 = 31+89 = 37+83 = 41+79 = 47+73 = 53+67 = 59+61 = 61+59 = 67+53 = 73+47 = 79+41 = 83+37 = 89+31 = 97+23 = 101+19 = 103+17 = 107+13 = 109+11 = 113+7 (# 24) 122 = 13+109 = 19+103 = 43+79 = 61+61 = 79+43 = 103+19 = 109+13 (# 7) 124 = 11+113 = 17+107 = 23+101 = 41+83 = 53+71 = 71+53 = 83+41 = 101+23 = 107+17 = 113+11 (# 10) 126 = 13+113 = 17+109 = 19+107 = 23+103 = 29+97 = 37+89 = 43+83 = 47+79 = 53+73 = 59+67 = 67+59 = 73+53 = 79+47 = 83+43 = 89+37 = 97+29 = 103+23 = 107+19 = 109+17 = 113+13 (# 20) 128 = 19+109 = 31+97 = 61+67 = 67+61 = 97+31 = 109+19 (# 6) 130 = 3+127 = 17+113 = 23+107 = 29+101 = 41+89 = 47+83 = 59+71 = 71+59 = 83+47 = 89+41 = 101+29 = 107+23 = 113+17 = 127+3 (# 14) 132 = 5+127 = 19+113 = 23+109 = 29+103 = 31+101 = 43+89 = 53+79 = 59+73 = 61+71 = 71+61 = 73+59 = 79+53 = 89+43 = 101+31 = 103+29 = 109+23 = 113+19 = 127+5 (# 18) 134 = 3+131 = 7+127 = 31+103 = 37+97 = 61+73 = 67+67 = 73+61 = 97+37 = 103+31 = 127+7 = 131+3 (# 11) 136 = 5+131 = 23+113 = 29+107 = 47+89 = 53+83 = 83+53 = 89+47 = 107+29 = 113+23 = 131+5 (# 10) 138 = 7+131 = 11+127 = 29+109 = 31+107 = 37+101 = 41+97 = 59+79 = 67+71 = 71+67 = 79+59 = 97+41 = 101+37 = 107+31 = 109+29 = 127+11 = 131+7 (# 16) 140 = 3+137 = 13+127 = 31+109 = 37+103 = 43+97 = 61+79 = 67+73 = 73+67 = 79+61 = 97+43 = 103+37 = 109+31 = 127+13 = 137+3 (# 14) 142 = 3+139 = 5+137 = 11+131 = 29+113 = 41+101 = 53+89 = 59+83 = 71+71 = 83+59 = 89+53 = 101+41 = 113+29 = 131+11 = 137+5 = 139+3 (# 15) 144 = 5+139 = 7+137 = 13+131 = 17+127 = 31+113 = 37+107 = 41+103 = 43+101 = 47+97 = 61+83 = 71+73 = 73+71 = 83+61 = 97+47 = 101+43 = 103+41 = 107+37 = 113+31 = 127+17 = 131+13 = 137+7 = 139+5 (# 22) 146 = 7+139 = 19+127 = 37+109 = 43+103 = 67+79 = 73+73 = 79+67 = 103+43 = 109+37 = 127+19 = 139+7 (# 11) 148 = 11+137 = 17+131 = 41+107 = 47+101 = 59+89 = 89+59 = 101+47 = 107+41 = 131+17 = 137+11 (# 10) 150 = 11+139 = 13+137 = 19+131 = 23+127 = 37+113 = 41+109 = 43+107 = 47+103 = 53+97 = 61+89 = 67+83 = 71+79 = 79+71 = 83+67 = 89+61 = 97+53 = 103+47 = 107+43 = 109+41 = 113+37 = 127+23 = 131+19 = 137+13 = 139+11 (# 24) 152 = 3+149 = 13+139 = 43+109 = 73+79 = 79+73 = 109+43 = 139+13 = 149+3 (# 8) 154 = 3+151 = 5+149 = 17+137 = 23+131 = 41+113 = 47+107 = 53+101 = 71+83 = 83+71 = 101+53 = 107+47 = 113+41 = 131+23 = 137+17 = 149+5 = 151+3 (# 16) 156 = 5+151 = 7+149 = 17+139 = 19+137 = 29+127 = 43+113 = 47+109 = 53+103 = 59+97 = 67+89 = 73+83 = 83+73 = 89+67 = 97+59 = 103+53 = 109+47 = 113+43 = 127+29 = 137+19 = 139+17 = 149+7 = 151+5 (# 22) 158 = 7+151 = 19+139 = 31+127 = 61+97 = 79+79 = 97+61 = 127+31 = 139+19 = 151+7 (# 9) 160 = 3+157 = 11+149 = 23+137 = 29+131 = 47+113 = 53+107 = 59+101 = 71+89 = 89+71 = 101+59 = 107+53 = 113+47 = 131+29 = 137+23 = 149+11 = 157+3 (# 16) 162 = 5+157 = 11+151 = 13+149 = 23+139 = 31+131 = 53+109 = 59+103 = 61+101 = 73+89 = 79+83 = 83+79 = 89+73 = 101+61 = 103+59 = 109+53 = 131+31 = 139+23 = 149+13 = 151+11 = 157+5 (# 20) 164 = 7+157 = 13+151 = 37+127 = 61+103 = 67+97 = 97+67 = 103+61 = 127+37 = 151+13 = 157+7 (# 10) 166 = 3+163 = 17+149 = 29+137 = 53+113 = 59+107 = 83+83 = 107+59 = 113+53 = 137+29 = 149+17 = 163+3 (# 11) 168 = 5+163 = 11+157 = 17+151 = 19+149 = 29+139 = 31+137 = 37+131 = 41+127 = 59+109 = 61+107 = 67+101 = 71+97 = 79+89 = 89+79 = 97+71 = 101+67 = 107+61 = 109+59 = 127+41 = 131+37 = 137+31 = 139+29 = 149+19 = 151+17 = 157+11 = 163+5 (# 26) 170 = 3+167 = 7+163 = 13+157 = 19+151 = 31+139 = 43+127 = 61+109 = 67+103 = 73+97 = 97+73 = 103+67 = 109+61 = 127+43 = 139+31 = 151+19 = 157+13 = 163+7 = 167+3 (# 18) 172 = 5+167 = 23+149 = 41+131 = 59+113 = 71+101 = 83+89 = 89+83 = 101+71 = 113+59 = 131+41 = 149+23 = 167+5 (# 12) 174 = 7+167 = 11+163 = 17+157 = 23+151 = 37+137 = 43+131 = 47+127 = 61+113 = 67+107 = 71+103 = 73+101 = 101+73 = 103+71 = 107+67 = 113+61 = 127+47 = 131+43 = 137+37 = 151+23 = 157+17 = 163+11 = 167+7 (# 22) 176 = 3+173 = 13+163 = 19+157 = 37+139 = 67+109 = 73+103 = 79+97 = 97+79 = 103+73 = 109+67 = 139+37 = 157+19 = 163+13 = 173+3 (# 14) 178 = 5+173 = 11+167 = 29+149 = 41+137 = 47+131 = 71+107 = 89+89 = 107+71 = 131+47 = 137+41 = 149+29 = 167+11 = 173+5 (# 13) 180 = 7+173 = 13+167 = 17+163 = 23+157 = 29+151 = 31+149 = 41+139 = 43+137 = 53+127 = 67+113 = 71+109 = 73+107 = 79+101 = 83+97 = 97+83 = 101+79 = 107+73 = 109+71 = 113+67 = 127+53 = 137+43 = 139+41 = 149+31 = 151+29 = 157+23 = 163+17 = 167+13 = 173+7 (# 28) 182 = 3+179 = 19+163 = 31+151 = 43+139 = 73+109 = 79+103 = 103+79 = 109+73 = 139+43 = 151+31 = 163+19 = 179+3 (# 12) 184 = 3+181 = 5+179 = 11+173 = 17+167 = 47+137 = 53+131 = 71+113 = 83+101 = 101+83 = 113+71 = 131+53 = 137+47 = 167+17 = 173+11 = 179+5 = 181+3 (# 16) 186 = 5+181 = 7+179 = 13+173 = 19+167 = 23+163 = 29+157 = 37+149 = 47+139 = 59+127 = 73+113 = 79+107 = 83+103 = 89+97 = 97+89 = 103+83 = 107+79 = 113+73 = 127+59 = 139+47 = 149+37 = 157+29 = 163+23 = 167+19 = 173+13 = 179+7 = 181+5 (# 26) 188 = 7+181 = 31+157 = 37+151 = 61+127 = 79+109 = 109+79 = 127+61 = 151+37 = 157+31 = 181+7 (# 10) 190 = 11+179 = 17+173 = 23+167 = 41+149 = 53+137 = 59+131 = 83+107 = 89+101 = 101+89 = 107+83 = 131+59 = 137+53 = 149+41 = 167+23 = 173+17 = 179+11 (# 16) 192 = 11+181 = 13+179 = 19+173 = 29+163 = 41+151 = 43+149 = 53+139 = 61+131 = 79+113 = 83+109 = 89+103 = 103+89 = 109+83 = 113+79 = 131+61 = 139+53 = 149+43 = 151+41 = 163+29 = 173+19 = 179+13 = 181+11 (# 22) 194 = 3+191 = 13+181 = 31+163 = 37+157 = 43+151 = 67+127 = 97+97 = 127+67 = 151+43 = 157+37 = 163+31 = 181+13 = 191+3 (# 13) 196 = 3+193 = 5+191 = 17+179 = 23+173 = 29+167 = 47+149 = 59+137 = 83+113 = 89+107 = 107+89 = 113+83 = 137+59 = 149+47 = 167+29 = 173+23 = 179+17 = 191+5 = 193+3 (# 18) 198 = 5+193 = 7+191 = 17+181 = 19+179 = 31+167 = 41+157 = 47+151 = 59+139 = 61+137 = 67+131 = 71+127 = 89+109 = 97+101 = 101+97 = 109+89 = 127+71 = 131+67 = 137+61 = 139+59 = 151+47 = 157+41 = 167+31 = 179+19 = 181+17 = 191+7 = 193+5 (# 26) 200 = 3+197 = 7+193 = 19+181 = 37+163 = 43+157 = 61+139 = 73+127 = 97+103 = 103+97 = 127+73 = 139+61 = 157+43 = 163+37 = 181+19 = 193+7 = 197+3 (# 16) 202 = 3+199 = 5+197 = 11+191 = 23+179 = 29+173 = 53+149 = 71+131 = 89+113 = 101+101 = 113+89 = 131+71 = 149+53 = 173+29 = 179+23 = 191+11 = 197+5 = 199+3 (# 17) 204 = 5+199 = 7+197 = 11+193 = 13+191 = 23+181 = 31+173 = 37+167 = 41+163 = 47+157 = 53+151 = 67+137 = 73+131 = 97+107 = 101+103 = 103+101 = 107+97 = 131+73 = 137+67 = 151+53 = 157+47 = 163+41 = 167+37 = 173+31 = 181+23 = 191+13 = 193+11 = 197+7 = 199+5 (# 28) 206 = 7+199 = 13+193 = 43+163 = 67+139 = 79+127 = 97+109 = 103+103 = 109+97 = 127+79 = 139+67 = 163+43 = 193+13 = 199+7 (# 13) 208 = 11+197 = 17+191 = 29+179 = 41+167 = 59+149 = 71+137 = 101+107 = 107+101 = 137+71 = 149+59 = 167+41 = 179+29 = 191+17 = 197+11 (# 14) 210 = 11+199 = 13+197 = 17+193 = 19+191 = 29+181 = 31+179 = 37+173 = 43+167 = 47+163 = 53+157 = 59+151 = 61+149 = 71+139 = 73+137 = 79+131 = 83+127 = 97+113 = 101+109 = 103+107 = 107+103 = 109+101 = 113+97 = 127+83 = 131+79 = 137+73 = 139+71 = 149+61 = 151+59 = 157+53 = 163+47 = 167+43 = 173+37 = 179+31 = 181+29 = 191+19 = 193+17 = 197+13 = 199+11 (# 38) 212 = 13+199 = 19+193 = 31+181 = 61+151 = 73+139 = 103+109 = 109+103 = 139+73 = 151+61 = 181+31 = 193+19 = 199+13 (# 12) 214 = 3+211 = 17+197 = 23+191 = 41+173 = 47+167 = 83+131 = 101+113 = 107+107 = 113+101 = 131+83 = 167+47 = 173+41 = 191+23 = 197+17 = 211+3 (# 15) 216 = 5+211 = 17+199 = 19+197 = 23+193 = 37+179 = 43+173 = 53+163 = 59+157 = 67+149 = 79+137 = 89+127 = 103+113 = 107+109 = 109+107 = 113+103 = 127+89 = 137+79 = 149+67 = 157+59 = 163+53 = 173+43 = 179+37 = 193+23 = 197+19 = 199+17 = 211+5 (# 26) 218 = 7+211 = 19+199 = 37+181 = 61+157 = 67+151 = 79+139 = 109+109 = 139+79 = 151+67 = 157+61 = 181+37 = 199+19 = 211+7 (# 13) 220 = 23+197 = 29+191 = 41+179 = 47+173 = 53+167 = 71+149 = 83+137 = 89+131 = 107+113 = 113+107 = 131+89 = 137+83 = 149+71 = 167+53 = 173+47 = 179+41 = 191+29 = 197+23 (# 18) 222 = 11+211 = 23+199 = 29+193 = 31+191 = 41+181 = 43+179 = 59+163 = 71+151 = 73+149 = 83+139 = 109+113 = 113+109 = 139+83 = 149+73 = 151+71 = 163+59 = 179+43 = 181+41 = 191+31 = 193+29 = 199+23 = 211+11 (# 22) 224 = 13+211 = 31+193 = 43+181 = 61+163 = 67+157 = 73+151 = 97+127 = 127+97 = 151+73 = 157+67 = 163+61 = 181+43 = 193+31 = 211+13 (# 14) 226 = 3+223 = 29+197 = 47+179 = 53+173 = 59+167 = 89+137 = 113+113 = 137+89 = 167+59 = 173+53 = 179+47 = 197+29 = 223+3 (# 13) 228 = 5+223 = 17+211 = 29+199 = 31+197 = 37+191 = 47+181 = 61+167 = 71+157 = 79+149 = 89+139 = 97+131 = 101+127 = 127+101 = 131+97 = 139+89 = 149+79 = 157+71 = 167+61 = 181+47 = 191+37 = 197+31 = 199+29 = 211+17 = 223+5 (# 24) 230 = 3+227 = 7+223 = 19+211 = 31+199 = 37+193 = 67+163 = 73+157 = 79+151 = 103+127 = 127+103 = 151+79 = 157+73 = 163+67 = 193+37 = 199+31 = 211+19 = 223+7 = 227+3 (# 18) 232 = 3+229 = 5+227 = 41+191 = 53+179 = 59+173 = 83+149 = 101+131 = 131+101 = 149+83 = 173+59 = 179+53 = 191+41 = 227+5 = 229+3 (# 14) 234 = 5+229 = 7+227 = 11+223 = 23+211 = 37+197 = 41+193 = 43+191 = 53+181 = 61+173 = 67+167 = 71+163 = 83+151 = 97+137 = 103+131 = 107+127 = 127+107 = 131+103 = 137+97 = 151+83 = 163+71 = 167+67 = 173+61 = 181+53 = 191+43 = 193+41 = 197+37 = 211+23 = 223+11 = 227+7 = 229+5 (# 30) 236 = 3+233 = 7+229 = 13+223 = 37+199 = 43+193 = 73+163 = 79+157 = 97+139 = 109+127 = 127+109 = 139+97 = 157+79 = 163+73 = 193+43 = 199+37 = 223+13 = 229+7 = 233+3 (# 18) 238 = 5+233 = 11+227 = 41+197 = 47+191 = 59+179 = 71+167 = 89+149 = 101+137 = 107+131 = 131+107 = 137+101 = 149+89 = 167+71 = 179+59 = 191+47 = 197+41 = 227+11 = 233+5 (# 18) 240 = 7+233 = 11+229 = 13+227 = 17+223 = 29+211 = 41+199 = 43+197 = 47+193 = 59+181 = 61+179 = 67+173 = 73+167 = 83+157 = 89+151 = 101+139 = 103+137 = 109+131 = 113+127 = 127+113 = 131+109 = 137+103 = 139+101 = 151+89 = 157+83 = 167+73 = 173+67 = 179+61 = 181+59 = 193+47 = 197+43 = 199+41 = 211+29 = 223+17 = 227+13 = 229+11 = 233+7 (# 36) 242 = 3+239 = 13+229 = 19+223 = 31+211 = 43+199 = 61+181 = 79+163 = 103+139 = 139+103 = 163+79 = 181+61 = 199+43 = 211+31 = 223+19 = 229+13 = 239+3 (# 16) 244 = 3+241 = 5+239 = 11+233 = 17+227 = 47+197 = 53+191 = 71+173 = 107+137 = 113+131 = 131+113 = 137+107 = 173+71 = 191+53 = 197+47 = 227+17 = 233+11 = 239+5 = 241+3 (# 18) 246 = 5+241 = 7+239 = 13+233 = 17+229 = 19+227 = 23+223 = 47+199 = 53+193 = 67+179 = 73+173 = 79+167 = 83+163 = 89+157 = 97+149 = 107+139 = 109+137 = 137+109 = 139+107 = 149+97 = 157+89 = 163+83 = 167+79 = 173+73 = 179+67 = 193+53 = 199+47 = 223+23 = 227+19 = 229+17 = 233+13 = 239+7 = 241+5 (# 32) 248 = 7+241 = 19+229 = 37+211 = 67+181 = 97+151 = 109+139 = 139+109 = 151+97 = 181+67 = 211+37 = 229+19 = 241+7 (# 12) 250 = 11+239 = 17+233 = 23+227 = 53+197 = 59+191 = 71+179 = 83+167 = 101+149 = 113+137 = 137+113 = 149+101 = 167+83 = 179+71 = 191+59 = 197+53 = 227+23 = 233+17 = 239+11 (# 18) 252 = 11+241 = 13+239 = 19+233 = 23+229 = 29+223 = 41+211 = 53+199 = 59+193 = 61+191 = 71+181 = 73+179 = 79+173 = 89+163 = 101+151 = 103+149 = 113+139 = 139+113 = 149+103 = 151+101 = 163+89 = 173+79 = 179+73 = 181+71 = 191+61 = 193+59 = 199+53 = 211+41 = 223+29 = 229+23 = 233+19 = 239+13 = 241+11 (# 32) 254 = 3+251 = 13+241 = 31+223 = 43+211 = 61+193 = 73+181 = 97+157 = 103+151 = 127+127 = 151+103 = 157+97 = 181+73 = 193+61 = 211+43 = 223+31 = 241+13 = 251+3 (# 17) 256 = 5+251 = 17+239 = 23+233 = 29+227 = 59+197 = 83+173 = 89+167 = 107+149 = 149+107 = 167+89 = 173+83 = 197+59 = 227+29 = 233+23 = 239+17 = 251+5 (# 16) 258 = 7+251 = 17+241 = 19+239 = 29+229 = 31+227 = 47+211 = 59+199 = 61+197 = 67+191 = 79+179 = 101+157 = 107+151 = 109+149 = 127+131 = 131+127 = 149+109 = 151+107 = 157+101 = 179+79 = 191+67 = 197+61 = 199+59 = 211+47 = 227+31 = 229+29 = 239+19 = 241+17 = 251+7 (# 28) 260 = 3+257 = 19+241 = 31+229 = 37+223 = 61+199 = 67+193 = 79+181 = 97+163 = 103+157 = 109+151 = 151+109 = 157+103 = 163+97 = 181+79 = 193+67 = 199+61 = 223+37 = 229+31 = 241+19 = 257+3 (# 20) 262 = 5+257 = 11+251 = 23+239 = 29+233 = 71+191 = 83+179 = 89+173 = 113+149 = 131+131 = 149+113 = 173+89 = 179+83 = 191+71 = 233+29 = 239+23 = 251+11 = 257+5 (# 17) 264 = 7+257 = 13+251 = 23+241 = 31+233 = 37+227 = 41+223 = 53+211 = 67+197 = 71+193 = 73+191 = 83+181 = 97+167 = 101+163 = 107+157 = 113+151 = 127+137 = 137+127 = 151+113 = 157+107 = 163+101 = 167+97 = 181+83 = 191+73 = 193+71 = 197+67 = 211+53 = 223+41 = 227+37 = 233+31 = 241+23 = 251+13 = 257+7 (# 32) 266 = 3+263 = 37+229 = 43+223 = 67+199 = 73+193 = 103+163 = 109+157 = 127+139 = 139+127 = 157+109 = 163+103 = 193+73 = 199+67 = 223+43 = 229+37 = 263+3 (# 16) 268 = 5+263 = 11+257 = 17+251 = 29+239 = 41+227 = 71+197 = 89+179 = 101+167 = 131+137 = 137+131 = 167+101 = 179+89 = 197+71 = 227+41 = 239+29 = 251+17 = 257+11 = 263+5 (# 18) 270 = 7+263 = 13+257 = 19+251 = 29+241 = 31+239 = 37+233 = 41+229 = 43+227 = 47+223 = 59+211 = 71+199 = 73+197 = 79+191 = 89+181 = 97+173 = 103+167 = 107+163 = 113+157 = 131+139 = 139+131 = 157+113 = 163+107 = 167+103 = 173+97 = 181+89 = 191+79 = 197+73 = 199+71 = 211+59 = 223+47 = 227+43 = 229+41 = 233+37 = 239+31 = 241+29 = 251+19 = 257+13 = 263+7 (# 38) 272 = 3+269 = 31+241 = 43+229 = 61+211 = 73+199 = 79+193 = 109+163 = 163+109 = 193+79 = 199+73 = 211+61 = 229+43 = 241+31 = 269+3 (# 14) 274 = 3+271 = 5+269 = 11+263 = 17+257 = 23+251 = 41+233 = 47+227 = 83+191 = 101+173 = 107+167 = 137+137 = 167+107 = 173+101 = 191+83 = 227+47 = 233+41 = 251+23 = 257+17 = 263+11 = 269+5 = 271+3 (# 21) 276 = 5+271 = 7+269 = 13+263 = 19+257 = 37+239 = 43+233 = 47+229 = 53+223 = 79+197 = 83+193 = 97+179 = 103+173 = 109+167 = 113+163 = 127+149 = 137+139 = 139+137 = 149+127 = 163+113 = 167+109 = 173+103 = 179+97 = 193+83 = 197+79 = 223+53 = 229+47 = 233+43 = 239+37 = 257+19 = 263+13 = 269+7 = 271+5 (# 32) 278 = 7+271 = 37+241 = 67+211 = 79+199 = 97+181 = 127+151 = 139+139 = 151+127 = 181+97 = 199+79 = 211+67 = 241+37 = 271+7 (# 13) 280 = 3+277 = 11+269 = 17+263 = 23+257 = 29+251 = 41+239 = 47+233 = 53+227 = 83+197 = 89+191 = 101+179 = 107+173 = 113+167 = 131+149 = 149+131 = 167+113 = 173+107 = 179+101 = 191+89 = 197+83 = 227+53 = 233+47 = 239+41 = 251+29 = 257+23 = 263+17 = 269+11 = 277+3 (# 28) 282 = 5+277 = 11+271 = 13+269 = 19+263 = 31+251 = 41+241 = 43+239 = 53+229 = 59+223 = 71+211 = 83+199 = 89+193 = 101+181 = 103+179 = 109+173 = 131+151 = 151+131 = 173+109 = 179+103 = 181+101 = 193+89 = 199+83 = 211+71 = 223+59 = 229+53 = 239+43 = 241+41 = 251+31 = 263+19 = 269+13 = 271+11 = 277+5 (# 32) 284 = 3+281 = 7+277 = 13+271 = 43+241 = 61+223 = 73+211 = 103+181 = 127+157 = 157+127 = 181+103 = 211+73 = 223+61 = 241+43 = 271+13 = 277+7 = 281+3 (# 16) 286 = 3+283 = 5+281 = 17+269 = 23+263 = 29+257 = 47+239 = 53+233 = 59+227 = 89+197 = 107+179 = 113+173 = 137+149 = 149+137 = 173+113 = 179+107 = 197+89 = 227+59 = 233+53 = 239+47 = 257+29 = 263+23 = 269+17 = 281+5 = 283+3 (# 24) 288 = 5+283 = 7+281 = 11+277 = 17+271 = 19+269 = 31+257 = 37+251 = 47+241 = 59+229 = 61+227 = 89+199 = 97+191 = 107+181 = 109+179 = 131+157 = 137+151 = 139+149 = 149+139 = 151+137 = 157+131 = 179+109 = 181+107 = 191+97 = 199+89 = 227+61 = 229+59 = 241+47 = 251+37 = 257+31 = 269+19 = 271+17 = 277+11 = 281+7 = 283+5 (# 34) 290 = 7+283 = 13+277 = 19+271 = 61+229 = 67+223 = 79+211 = 97+193 = 109+181 = 127+163 = 139+151 = 151+139 = 163+127 = 181+109 = 193+97 = 211+79 = 223+67 = 229+61 = 271+19 = 277+13 = 283+7 (# 20) 292 = 11+281 = 23+269 = 29+263 = 41+251 = 53+239 = 59+233 = 101+191 = 113+179 = 179+113 = 191+101 = 233+59 = 239+53 = 251+41 = 263+29 = 269+23 = 281+11 (# 16) 294 = 11+283 = 13+281 = 17+277 = 23+271 = 31+263 = 37+257 = 43+251 = 53+241 = 61+233 = 67+227 = 71+223 = 83+211 = 97+197 = 101+193 = 103+191 = 113+181 = 127+167 = 131+163 = 137+157 = 157+137 = 163+131 = 167+127 = 181+113 = 191+103 = 193+101 = 197+97 = 211+83 = 223+71 = 227+67 = 233+61 = 241+53 = 251+43 = 257+37 = 263+31 = 271+23 = 277+17 = 281+13 = 283+11 (# 38) 296 = 3+293 = 13+283 = 19+277 = 67+229 = 73+223 = 97+199 = 103+193 = 139+157 = 157+139 = 193+103 = 199+97 = 223+73 = 229+67 = 277+19 = 283+13 = 293+3 (# 16) 298 = 5+293 = 17+281 = 29+269 = 41+257 = 47+251 = 59+239 = 71+227 = 101+197 = 107+191 = 131+167 = 149+149 = 167+131 = 191+107 = 197+101 = 227+71 = 239+59 = 251+47 = 257+41 = 269+29 = 281+17 = 293+5 (# 21) 300 = 7+293 = 17+283 = 19+281 = 23+277 = 29+271 = 31+269 = 37+263 = 43+257 = 59+241 = 61+239 = 67+233 = 71+229 = 73+227 = 89+211 = 101+199 = 103+197 = 107+193 = 109+191 = 127+173 = 137+163 = 149+151 = 151+149 = 163+137 = 173+127 = 191+109 = 193+107 = 197+103 = 199+101 = 211+89 = 227+73 = 229+71 = 233+67 = 239+61 = 241+59 = 257+43 = 263+37 = 269+31 = 271+29 = 277+23 = 281+19 = 283+17 = 293+7 (# 42) 302 = 19+283 = 31+271 = 61+241 = 73+229 = 79+223 = 103+199 = 109+193 = 139+163 = 151+151 = 163+139 = 193+109 = 199+103 = 223+79 = 229+73 = 241+61 = 271+31 = 283+19 (# 17) 304 = 11+293 = 23+281 = 41+263 = 47+257 = 53+251 = 71+233 = 107+197 = 113+191 = 131+173 = 137+167 = 167+137 = 173+131 = 191+113 = 197+107 = 233+71 = 251+53 = 257+47 = 263+41 = 281+23 = 293+11 (# 20) 306 = 13+293 = 23+283 = 29+277 = 37+269 = 43+263 = 67+239 = 73+233 = 79+227 = 83+223 = 107+199 = 109+197 = 113+193 = 127+179 = 139+167 = 149+157 = 157+149 = 167+139 = 179+127 = 193+113 = 197+109 = 199+107 = 223+83 = 227+79 = 233+73 = 239+67 = 263+43 = 269+37 = 277+29 = 283+23 = 293+13 (# 30) 308 = 31+277 = 37+271 = 67+241 = 79+229 = 97+211 = 109+199 = 127+181 = 151+157 = 157+151 = 181+127 = 199+109 = 211+97 = 229+79 = 241+67 = 271+37 = 277+31 (# 16) 310 = 3+307 = 17+293 = 29+281 = 41+269 = 47+263 = 53+257 = 59+251 = 71+239 = 83+227 = 113+197 = 131+179 = 137+173 = 173+137 = 179+131 = 197+113 = 227+83 = 239+71 = 251+59 = 257+53 = 263+47 = 269+41 = 281+29 = 293+17 = 307+3 (# 24) 312 = 5+307 = 19+293 = 29+283 = 31+281 = 41+271 = 43+269 = 61+251 = 71+241 = 73+239 = 79+233 = 83+229 = 89+223 = 101+211 = 113+199 = 131+181 = 139+173 = 149+163 = 163+149 = 173+139 = 181+131 = 199+113 = 211+101 = 223+89 = 229+83 = 233+79 = 239+73 = 241+71 = 251+61 = 269+43 = 271+41 = 281+31 = 283+29 = 293+19 = 307+5 (# 34) 314 = 3+311 = 7+307 = 31+283 = 37+277 = 43+271 = 73+241 = 103+211 = 151+163 = 157+157 = 163+151 = 211+103 = 241+73 = 271+43 = 277+37 = 283+31 = 307+7 = 311+3 (# 17) 316 = 3+313 = 5+311 = 23+293 = 47+269 = 53+263 = 59+257 = 83+233 = 89+227 = 137+179 = 149+167 = 167+149 = 179+137 = 227+89 = 233+83 = 257+59 = 263+53 = 269+47 = 293+23 = 311+5 = 313+3 (# 20) 318 = 5+313 = 7+311 = 11+307 = 37+281 = 41+277 = 47+271 = 61+257 = 67+251 = 79+239 = 89+229 = 107+211 = 127+191 = 137+181 = 139+179 = 151+167 = 167+151 = 179+139 = 181+137 = 191+127 = 211+107 = 229+89 = 239+79 = 251+67 = 257+61 = 271+47 = 277+41 = 281+37 = 307+11 = 311+7 = 313+5 (# 30) 320 = 3+317 = 7+313 = 13+307 = 37+283 = 43+277 = 79+241 = 97+223 = 109+211 = 127+193 = 139+181 = 157+163 = 163+157 = 181+139 = 193+127 = 211+109 = 223+97 = 241+79 = 277+43 = 283+37 = 307+13 = 313+7 = 317+3 (# 22) 322 = 5+317 = 11+311 = 29+293 = 41+281 = 53+269 = 59+263 = 71+251 = 83+239 = 89+233 = 131+191 = 149+173 = 173+149 = 191+131 = 233+89 = 239+83 = 251+71 = 263+59 = 269+53 = 281+41 = 293+29 = 311+11 = 317+5 (# 22) 324 = 7+317 = 11+313 = 13+311 = 17+307 = 31+293 = 41+283 = 43+281 = 47+277 = 53+271 = 61+263 = 67+257 = 73+251 = 83+241 = 97+227 = 101+223 = 113+211 = 127+197 = 131+193 = 151+173 = 157+167 = 167+157 = 173+151 = 193+131 = 197+127 = 211+113 = 223+101 = 227+97 = 241+83 = 251+73 = 257+67 = 263+61 = 271+53 = 277+47 = 281+43 = 283+41 = 293+31 = 307+17 = 311+13 = 313+11 = 317+7 (# 40) 326 = 13+313 = 19+307 = 43+283 = 97+229 = 103+223 = 127+199 = 163+163 = 199+127 = 223+103 = 229+97 = 283+43 = 307+19 = 313+13 (# 13) 328 = 11+317 = 17+311 = 47+281 = 59+269 = 71+257 = 89+239 = 101+227 = 131+197 = 137+191 = 149+179 = 179+149 = 191+137 = 197+131 = 227+101 = 239+89 = 257+71 = 269+59 = 281+47 = 311+17 = 317+11 (# 20) 330 = 13+317 = 17+313 = 19+311 = 23+307 = 37+293 = 47+283 = 53+277 = 59+271 = 61+269 = 67+263 = 73+257 = 79+251 = 89+241 = 97+233 = 101+229 = 103+227 = 107+223 = 131+199 = 137+193 = 139+191 = 149+181 = 151+179 = 157+173 = 163+167 = 167+163 = 173+157 = 179+151 = 181+149 = 191+139 = 193+137 = 199+131 = 223+107 = 227+103 = 229+101 = 233+97 = 241+89 = 251+79 = 257+73 = 263+67 = 269+61 = 271+59 = 277+53 = 283+47 = 293+37 = 307+23 = 311+19 = 313+17 = 317+13 (# 48) 332 = 19+313 = 61+271 = 103+229 = 109+223 = 139+193 = 151+181 = 181+151 = 193+139 = 223+109 = 229+103 = 271+61 = 313+19 (# 12) 334 = 3+331 = 17+317 = 23+311 = 41+293 = 53+281 = 71+263 = 83+251 = 101+233 = 107+227 = 137+197 = 167+167 = 197+137 = 227+107 = 233+101 = 251+83 = 263+71 = 281+53 = 293+41 = 311+23 = 317+17 = 331+3 (# 21) 336 = 5+331 = 19+317 = 23+313 = 29+307 = 43+293 = 53+283 = 59+277 = 67+269 = 73+263 = 79+257 = 97+239 = 103+233 = 107+229 = 109+227 = 113+223 = 137+199 = 139+197 = 157+179 = 163+173 = 173+163 = 179+157 = 197+139 = 199+137 = 223+113 = 227+109 = 229+107 = 233+103 = 239+97 = 257+79 = 263+73 = 269+67 = 277+59 = 283+53 = 293+43 = 307+29 = 313+23 = 317+19 = 331+5 (# 38) 338 = 7+331 = 31+307 = 61+277 = 67+271 = 97+241 = 109+229 = 127+211 = 139+199 = 157+181 = 181+157 = 199+139 = 211+127 = 229+109 = 241+97 = 271+67 = 277+61 = 307+31 = 331+7 (# 18) 340 = 3+337 = 23+317 = 29+311 = 47+293 = 59+281 = 71+269 = 83+257 = 89+251 = 101+239 = 107+233 = 113+227 = 149+191 = 167+173 = 173+167 = 191+149 = 227+113 = 233+107 = 239+101 = 251+89 = 257+83 = 269+71 = 281+59 = 293+47 = 311+29 = 317+23 = 337+3 (# 26) 342 = 5+337 = 11+331 = 29+313 = 31+311 = 59+283 = 61+281 = 71+271 = 73+269 = 79+263 = 101+241 = 103+239 = 109+233 = 113+229 = 131+211 = 149+193 = 151+191 = 163+179 = 179+163 = 191+151 = 193+149 = 211+131 = 229+113 = 233+109 = 239+103 = 241+101 = 263+79 = 269+73 = 271+71 = 281+61 = 283+59 = 311+31 = 313+29 = 331+11 = 337+5 (# 34) 344 = 7+337 = 13+331 = 31+313 = 37+307 = 61+283 = 67+277 = 73+271 = 103+241 = 151+193 = 163+181 = 181+163 = 193+151 = 241+103 = 271+73 = 277+67 = 283+61 = 307+37 = 313+31 = 331+13 = 337+7 (# 20) 346 = 29+317 = 53+293 = 83+263 = 89+257 = 107+239 = 113+233 = 149+197 = 167+179 = 173+173 = 179+167 = 197+149 = 233+113 = 239+107 = 257+89 = 263+83 = 293+53 = 317+29 (# 17) 348 = 11+337 = 17+331 = 31+317 = 37+311 = 41+307 = 67+281 = 71+277 = 79+269 = 97+251 = 107+241 = 109+239 = 137+211 = 149+199 = 151+197 = 157+191 = 167+181 = 181+167 = 191+157 = 197+151 = 199+149 = 211+137 = 239+109 = 241+107 = 251+97 = 269+79 = 277+71 = 281+67 = 307+41 = 311+37 = 317+31 = 331+17 = 337+11 (# 32) 350 = 3+347 = 13+337 = 19+331 = 37+313 = 43+307 = 67+283 = 73+277 = 79+271 = 109+241 = 127+223 = 139+211 = 151+199 = 157+193 = 193+157 = 199+151 = 211+139 = 223+127 = 241+109 = 271+79 = 277+73 = 283+67 = 307+43 = 313+37 = 331+19 = 337+13 = 347+3 (# 26) 352 = 3+349 = 5+347 = 41+311 = 59+293 = 71+281 = 83+269 = 89+263 = 101+251 = 113+239 = 173+179 = 179+173 = 239+113 = 251+101 = 263+89 = 269+83 = 281+71 = 293+59 = 311+41 = 347+5 = 349+3 (# 20) 354 = 5+349 = 7+347 = 17+337 = 23+331 = 37+317 = 41+313 = 43+311 = 47+307 = 61+293 = 71+283 = 73+281 = 83+271 = 97+257 = 103+251 = 113+241 = 127+227 = 131+223 = 157+197 = 163+191 = 173+181 = 181+173 = 191+163 = 197+157 = 223+131 = 227+127 = 241+113 = 251+103 = 257+97 = 271+83 = 281+73 = 283+71 = 293+61 = 307+47 = 311+43 = 313+41 = 317+37 = 331+23 = 337+17 = 347+7 = 349+5 (# 40) 356 = 3+353 = 7+349 = 19+337 = 43+313 = 73+283 = 79+277 = 127+229 = 157+199 = 163+193 = 193+163 = 199+157 = 229+127 = 277+79 = 283+73 = 313+43 = 337+19 = 349+7 = 353+3 (# 18) 358 = 5+353 = 11+347 = 41+317 = 47+311 = 89+269 = 101+257 = 107+251 = 131+227 = 167+191 = 179+179 = 191+167 = 227+131 = 251+107 = 257+101 = 269+89 = 311+47 = 317+41 = 347+11 = 353+5 (# 19) 360 = 7+353 = 11+349 = 13+347 = 23+337 = 29+331 = 43+317 = 47+313 = 53+307 = 67+293 = 79+281 = 83+277 = 89+271 = 97+263 = 103+257 = 109+251 = 127+233 = 131+229 = 137+223 = 149+211 = 163+197 = 167+193 = 179+181 = 181+179 = 193+167 = 197+163 = 211+149 = 223+137 = 229+131 = 233+127 = 251+109 = 257+103 = 263+97 = 271+89 = 277+83 = 281+79 = 293+67 = 307+53 = 313+47 = 317+43 = 331+29 = 337+23 = 347+13 = 349+11 = 353+7 (# 44) 362 = 3+359 = 13+349 = 31+331 = 79+283 = 139+223 = 151+211 = 163+199 = 181+181 = 199+163 = 211+151 = 223+139 = 283+79 = 331+31 = 349+13 = 359+3 (# 15) 364 = 5+359 = 11+353 = 17+347 = 47+317 = 53+311 = 71+293 = 83+281 = 101+263 = 107+257 = 113+251 = 131+233 = 137+227 = 167+197 = 173+191 = 191+173 = 197+167 = 227+137 = 233+131 = 251+113 = 257+107 = 263+101 = 281+83 = 293+71 = 311+53 = 317+47 = 347+17 = 353+11 = 359+5 (# 28) 366 = 7+359 = 13+353 = 17+349 = 19+347 = 29+337 = 53+313 = 59+307 = 73+293 = 83+283 = 89+277 = 97+269 = 103+263 = 109+257 = 127+239 = 137+229 = 139+227 = 167+199 = 173+193 = 193+173 = 199+167 = 227+139 = 229+137 = 239+127 = 257+109 = 263+103 = 269+97 = 277+89 = 283+83 = 293+73 = 307+59 = 313+53 = 337+29 = 347+19 = 349+17 = 353+13 = 359+7 (# 36) 368 = 19+349 = 31+337 = 37+331 = 61+307 = 97+271 = 127+241 = 139+229 = 157+211 = 211+157 = 229+139 = 241+127 = 271+97 = 307+61 = 331+37 = 337+31 = 349+19 (# 16) 370 = 3+367 = 11+359 = 17+353 = 23+347 = 53+317 = 59+311 = 89+281 = 101+269 = 107+263 = 113+257 = 131+239 = 137+233 = 173+197 = 179+191 = 191+179 = 197+173 = 233+137 = 239+131 = 257+113 = 263+107 = 269+101 = 281+89 = 311+59 = 317+53 = 347+23 = 353+17 = 359+11 = 367+3 (# 28) 372 = 5+367 = 13+359 = 19+353 = 23+349 = 41+331 = 59+313 = 61+311 = 79+293 = 89+283 = 101+271 = 103+269 = 109+263 = 131+241 = 139+233 = 149+223 = 173+199 = 179+193 = 181+191 = 191+181 = 193+179 = 199+173 = 223+149 = 233+139 = 241+131 = 263+109 = 269+103 = 271+101 = 283+89 = 293+79 = 311+61 = 313+59 = 331+41 = 349+23 = 353+19 = 359+13 = 367+5 (# 36) 374 = 7+367 = 37+337 = 43+331 = 61+313 = 67+307 = 97+277 = 103+271 = 151+223 = 163+211 = 181+193 = 193+181 = 211+163 = 223+151 = 271+103 = 277+97 = 307+67 = 313+61 = 331+43 = 337+37 = 367+7 (# 20) 376 = 3+373 = 17+359 = 23+353 = 29+347 = 59+317 = 83+293 = 107+269 = 113+263 = 137+239 = 149+227 = 179+197 = 197+179 = 227+149 = 239+137 = 263+113 = 269+107 = 293+83 = 317+59 = 347+29 = 353+23 = 359+17 = 373+3 (# 22) 378 = 5+373 = 11+367 = 19+359 = 29+349 = 31+347 = 41+337 = 47+331 = 61+317 = 67+311 = 71+307 = 97+281 = 101+277 = 107+271 = 109+269 = 127+251 = 137+241 = 139+239 = 149+229 = 151+227 = 167+211 = 179+199 = 181+197 = 197+181 = 199+179 = 211+167 = 227+151 = 229+149 = 239+139 = 241+137 = 251+127 = 269+109 = 271+107 = 277+101 = 281+97 = 307+71 = 311+67 = 317+61 = 331+47 = 337+41 = 347+31 = 349+29 = 359+19 = 367+11 = 373+5 (# 44) 380 = 7+373 = 13+367 = 31+349 = 43+337 = 67+313 = 73+307 = 97+283 = 103+277 = 109+271 = 139+241 = 151+229 = 157+223 = 181+199 = 199+181 = 223+157 = 229+151 = 241+139 = 271+109 = 277+103 = 283+97 = 307+73 = 313+67 = 337+43 = 349+31 = 367+13 = 373+7 (# 26) 382 = 3+379 = 23+359 = 29+353 = 71+311 = 89+293 = 101+281 = 113+269 = 131+251 = 149+233 = 191+191 = 233+149 = 251+131 = 269+113 = 281+101 = 293+89 = 311+71 = 353+29 = 359+23 = 379+3 (# 19) 384 = 5+379 = 11+373 = 17+367 = 31+353 = 37+347 = 47+337 = 53+331 = 67+317 = 71+313 = 73+311 = 101+283 = 103+281 = 107+277 = 113+271 = 127+257 = 151+233 = 157+227 = 173+211 = 191+193 = 193+191 = 211+173 = 227+157 = 233+151 = 257+127 = 271+113 = 277+107 = 281+103 = 283+101 = 311+73 = 313+71 = 317+67 = 331+53 = 337+47 = 347+37 = 353+31 = 367+17 = 373+11 = 379+5 (# 38) 386 = 3+383 = 7+379 = 13+373 = 19+367 = 37+349 = 73+313 = 79+307 = 103+283 = 109+277 = 157+229 = 163+223 = 193+193 = 223+163 = 229+157 = 277+109 = 283+103 = 307+79 = 313+73 = 349+37 = 367+19 = 373+13 = 379+7 = 383+3 (# 23) 388 = 5+383 = 29+359 = 41+347 = 71+317 = 107+281 = 131+257 = 137+251 = 149+239 = 191+197 = 197+191 = 239+149 = 251+137 = 257+131 = 281+107 = 317+71 = 347+41 = 359+29 = 383+5 (# 18) 390 = 7+383 = 11+379 = 17+373 = 23+367 = 31+359 = 37+353 = 41+349 = 43+347 = 53+337 = 59+331 = 73+317 = 79+311 = 83+307 = 97+293 = 107+283 = 109+281 = 113+277 = 127+263 = 139+251 = 149+241 = 151+239 = 157+233 = 163+227 = 167+223 = 179+211 = 191+199 = 193+197 = 197+193 = 199+191 = 211+179 = 223+167 = 227+163 = 233+157 = 239+151 = 241+149 = 251+139 = 263+127 = 277+113 = 281+109 = 283+107 = 293+97 = 307+83 = 311+79 = 317+73 = 331+59 = 337+53 = 347+43 = 349+41 = 353+37 = 359+31 = 367+23 = 373+17 = 379+11 = 383+7 (# 54) 392 = 3+389 = 13+379 = 19+373 = 43+349 = 61+331 = 79+313 = 109+283 = 151+241 = 163+229 = 181+211 = 193+199 = 199+193 = 211+181 = 229+163 = 241+151 = 283+109 = 313+79 = 331+61 = 349+43 = 373+19 = 379+13 = 389+3 (# 22) 394 = 5+389 = 11+383 = 41+353 = 47+347 = 83+311 = 101+293 = 113+281 = 131+263 = 137+257 = 167+227 = 197+197 = 227+167 = 257+137 = 263+131 = 281+113 = 293+101 = 311+83 = 347+47 = 353+41 = 383+11 = 389+5 (# 21) 396 = 7+389 = 13+383 = 17+379 = 23+373 = 29+367 = 37+359 = 43+353 = 47+349 = 59+337 = 79+317 = 83+313 = 89+307 = 103+293 = 113+283 = 127+269 = 139+257 = 157+239 = 163+233 = 167+229 = 173+223 = 197+199 = 199+197 = 223+173 = 229+167 = 233+163 = 239+157 = 257+139 = 269+127 = 283+113 = 293+103 = 307+89 = 313+83 = 317+79 = 337+59 = 349+47 = 353+43 = 359+37 = 367+29 = 373+23 = 379+17 = 383+13 = 389+7 (# 42) 398 = 19+379 = 31+367 = 61+337 = 67+331 = 127+271 = 157+241 = 199+199 = 241+157 = 271+127 = 331+67 = 337+61 = 367+31 = 379+19 (# 13) 400 = 3+397 = 11+389 = 17+383 = 41+359 = 47+353 = 53+347 = 83+317 = 89+311 = 107+293 = 131+269 = 137+263 = 149+251 = 167+233 = 173+227 = 227+173 = 233+167 = 251+149 = 263+137 = 269+131 = 293+107 = 311+89 = 317+83 = 347+53 = 353+47 = 359+41 = 383+17 = 389+11 = 397+3 (# 28) 402 = 5+397 = 13+389 = 19+383 = 23+379 = 29+373 = 43+359 = 53+349 = 71+331 = 89+313 = 109+293 = 131+271 = 139+263 = 151+251 = 163+239 = 173+229 = 179+223 = 191+211 = 211+191 = 223+179 = 229+173 = 239+163 = 251+151 = 263+139 = 271+131 = 293+109 = 313+89 = 331+71 = 349+53 = 359+43 = 373+29 = 379+23 = 383+19 = 389+13 = 397+5 (# 34) 404 = 3+401 = 7+397 = 31+373 = 37+367 = 67+337 = 73+331 = 97+307 = 127+277 = 163+241 = 181+223 = 193+211 = 211+193 = 223+181 = 241+163 = 277+127 = 307+97 = 331+73 = 337+67 = 367+37 = 373+31 = 397+7 = 401+3 (# 22) 406 = 5+401 = 17+389 = 23+383 = 47+359 = 53+353 = 59+347 = 89+317 = 113+293 = 137+269 = 149+257 = 167+239 = 173+233 = 179+227 = 227+179 = 233+173 = 239+167 = 257+149 = 269+137 = 293+113 = 317+89 = 347+59 = 353+53 = 359+47 = 383+23 = 389+17 = 401+5 (# 26) 408 = 7+401 = 11+397 = 19+389 = 29+379 = 41+367 = 59+349 = 61+347 = 71+337 = 97+311 = 101+307 = 127+281 = 131+277 = 137+271 = 139+269 = 151+257 = 157+251 = 167+241 = 179+229 = 181+227 = 197+211 = 211+197 = 227+181 = 229+179 = 241+167 = 251+157 = 257+151 = 269+139 = 271+137 = 277+131 = 281+127 = 307+101 = 311+97 = 337+71 = 347+61 = 349+59 = 367+41 = 379+29 = 389+19 = 397+11 = 401+7 (# 40) 410 = 13+397 = 31+379 = 37+373 = 43+367 = 61+349 = 73+337 = 79+331 = 97+313 = 103+307 = 127+283 = 139+271 = 181+229 = 199+211 = 211+199 = 229+181 = 271+139 = 283+127 = 307+103 = 313+97 = 331+79 = 337+73 = 349+61 = 367+43 = 373+37 = 379+31 = 397+13 (# 26) 412 = 3+409 = 11+401 = 23+389 = 29+383 = 53+359 = 59+353 = 101+311 = 131+281 = 149+263 = 173+239 = 179+233 = 233+179 = 239+173 = 263+149 = 281+131 = 311+101 = 353+59 = 359+53 = 383+29 = 389+23 = 401+11 = 409+3 (# 22) 414 = 5+409 = 13+401 = 17+397 = 31+383 = 41+373 = 47+367 = 61+353 = 67+347 = 83+331 = 97+317 = 101+313 = 103+311 = 107+307 = 131+283 = 137+277 = 151+263 = 157+257 = 163+251 = 173+241 = 181+233 = 191+223 = 223+191 = 233+181 = 241+173 = 251+163 = 257+157 = 263+151 = 277+137 = 283+131 = 307+107 = 311+103 = 313+101 = 317+97 = 331+83 = 347+67 = 353+61 = 367+47 = 373+41 = 383+31 = 397+17 = 401+13 = 409+5 (# 42) 416 = 7+409 = 19+397 = 37+379 = 43+373 = 67+349 = 79+337 = 103+313 = 109+307 = 139+277 = 193+223 = 223+193 = 277+139 = 307+109 = 313+103 = 337+79 = 349+67 = 373+43 = 379+37 = 397+19 = 409+7 (# 20) 418 = 17+401 = 29+389 = 59+359 = 71+347 = 101+317 = 107+311 = 137+281 = 149+269 = 167+251 = 179+239 = 191+227 = 227+191 = 239+179 = 251+167 = 269+149 = 281+137 = 311+107 = 317+101 = 347+71 = 359+59 = 389+29 = 401+17 (# 22) 420 = 11+409 = 19+401 = 23+397 = 31+389 = 37+383 = 41+379 = 47+373 = 53+367 = 61+359 = 67+353 = 71+349 = 73+347 = 83+337 = 89+331 = 103+317 = 107+313 = 109+311 = 113+307 = 127+293 = 137+283 = 139+281 = 149+271 = 151+269 = 157+263 = 163+257 = 179+241 = 181+239 = 191+229 = 193+227 = 197+223 = 223+197 = 227+193 = 229+191 = 239+181 = 241+179 = 257+163 = 263+157 = 269+151 = 271+149 = 281+139 = 283+137 = 293+127 = 307+113 = 311+109 = 313+107 = 317+103 = 331+89 = 337+83 = 347+73 = 349+71 = 353+67 = 359+61 = 367+53 = 373+47 = 379+41 = 383+37 = 389+31 = 397+23 = 401+19 = 409+11 (# 60) 422 = 3+419 = 13+409 = 43+379 = 73+349 = 109+313 = 139+283 = 151+271 = 181+241 = 193+229 = 199+223 = 211+211 = 223+199 = 229+193 = 241+181 = 271+151 = 283+139 = 313+109 = 349+73 = 379+43 = 409+13 = 419+3 (# 21) 424 = 3+421 = 5+419 = 23+401 = 41+383 = 71+353 = 107+317 = 113+311 = 131+293 = 167+257 = 173+251 = 191+233 = 197+227 = 227+197 = 233+191 = 251+173 = 257+167 = 293+131 = 311+113 = 317+107 = 353+71 = 383+41 = 401+23 = 419+5 = 421+3 (# 24) 426 = 5+421 = 7+419 = 17+409 = 29+397 = 37+389 = 43+383 = 47+379 = 53+373 = 59+367 = 67+359 = 73+353 = 79+347 = 89+337 = 109+317 = 113+313 = 149+277 = 157+269 = 163+263 = 193+233 = 197+229 = 199+227 = 227+199 = 229+197 = 233+193 = 263+163 = 269+157 = 277+149 = 313+113 = 317+109 = 337+89 = 347+79 = 353+73 = 359+67 = 367+59 = 373+53 = 379+47 = 383+43 = 389+37 = 397+29 = 409+17 = 419+7 = 421+5 (# 42) 428 = 7+421 = 19+409 = 31+397 = 61+367 = 79+349 = 97+331 = 151+277 = 157+271 = 199+229 = 229+199 = 271+157 = 277+151 = 331+97 = 349+79 = 367+61 = 397+31 = 409+19 = 421+7 (# 18) 430 = 11+419 = 29+401 = 41+389 = 47+383 = 71+359 = 83+347 = 113+317 = 137+293 = 149+281 = 167+263 = 173+257 = 179+251 = 191+239 = 197+233 = 233+197 = 239+191 = 251+179 = 257+173 = 263+167 = 281+149 = 293+137 = 317+113 = 347+83 = 359+71 = 383+47 = 389+41 = 401+29 = 419+11 (# 28) 432 = 11+421 = 13+419 = 23+409 = 31+401 = 43+389 = 53+379 = 59+373 = 73+359 = 79+353 = 83+349 = 101+331 = 139+293 = 149+283 = 151+281 = 163+269 = 181+251 = 191+241 = 193+239 = 199+233 = 233+199 = 239+193 = 241+191 = 251+181 = 269+163 = 281+151 = 283+149 = 293+139 = 331+101 = 349+83 = 353+79 = 359+73 = 373+59 = 379+53 = 389+43 = 401+31 = 409+23 = 419+13 = 421+11 (# 38) 434 = 3+431 = 13+421 = 37+397 = 61+373 = 67+367 = 97+337 = 103+331 = 127+307 = 151+283 = 157+277 = 163+271 = 193+241 = 211+223 = 223+211 = 241+193 = 271+163 = 277+157 = 283+151 = 307+127 = 331+103 = 337+97 = 367+67 = 373+61 = 397+37 = 421+13 = 431+3 (# 26) 436 = 3+433 = 5+431 = 17+419 = 47+389 = 53+383 = 83+353 = 89+347 = 167+269 = 173+263 = 179+257 = 197+239 = 239+197 = 257+179 = 263+173 = 269+167 = 347+89 = 353+83 = 383+53 = 389+47 = 419+17 = 431+5 = 433+3 (# 22) 438 = 5+433 = 7+431 = 17+421 = 19+419 = 29+409 = 37+401 = 41+397 = 59+379 = 71+367 = 79+359 = 89+349 = 101+337 = 107+331 = 127+311 = 131+307 = 157+281 = 167+271 = 181+257 = 197+241 = 199+239 = 211+227 = 227+211 = 239+199 = 241+197 = 257+181 = 271+167 = 281+157 = 307+131 = 311+127 = 331+107 = 337+101 = 349+89 = 359+79 = 367+71 = 379+59 = 397+41 = 401+37 = 409+29 = 419+19 = 421+17 = 431+7 = 433+5 (# 42) 440 = 7+433 = 19+421 = 31+409 = 43+397 = 61+379 = 67+373 = 73+367 = 103+337 = 109+331 = 127+313 = 157+283 = 163+277 = 199+241 = 211+229 = 229+211 = 241+199 = 277+163 = 283+157 = 313+127 = 331+109 = 337+103 = 367+73 = 373+67 = 379+61 = 397+43 = 409+31 = 421+19 = 433+7 (# 28) 442 = 3+439 = 11+431 = 23+419 = 41+401 = 53+389 = 59+383 = 83+359 = 89+353 = 131+311 = 149+293 = 173+269 = 179+263 = 191+251 = 251+191 = 263+179 = 269+173 = 293+149 = 311+131 = 353+89 = 359+83 = 383+59 = 389+53 = 401+41 = 419+23 = 431+11 = 439+3 (# 26) 444 = 5+439 = 11+433 = 13+431 = 23+421 = 43+401 = 47+397 = 61+383 = 71+373 = 97+347 = 107+337 = 113+331 = 127+317 = 131+313 = 137+307 = 151+293 = 163+281 = 167+277 = 173+271 = 181+263 = 193+251 = 211+233 = 233+211 = 251+193 = 263+181 = 271+173 = 277+167 = 281+163 = 293+151 = 307+137 = 313+131 = 317+127 = 331+113 = 337+107 = 347+97 = 373+71 = 383+61 = 397+47 = 401+43 = 421+23 = 431+13 = 433+11 = 439+5 (# 42) 446 = 3+443 = 7+439 = 13+433 = 37+409 = 67+379 = 73+373 = 79+367 = 97+349 = 109+337 = 139+307 = 163+283 = 223+223 = 283+163 = 307+139 = 337+109 = 349+97 = 367+79 = 373+73 = 379+67 = 409+37 = 433+13 = 439+7 = 443+3 (# 23) 448 = 5+443 = 17+431 = 29+419 = 47+401 = 59+389 = 89+359 = 101+347 = 131+317 = 137+311 = 167+281 = 179+269 = 191+257 = 197+251 = 251+197 = 257+191 = 269+179 = 281+167 = 311+137 = 317+131 = 347+101 = 359+89 = 389+59 = 401+47 = 419+29 = 431+17 = 443+5 (# 26) 450 = 7+443 = 11+439 = 17+433 = 19+431 = 29+421 = 31+419 = 41+409 = 53+397 = 61+389 = 67+383 = 71+379 = 83+367 = 97+353 = 101+349 = 103+347 = 113+337 = 137+313 = 139+311 = 157+293 = 167+283 = 173+277 = 179+271 = 181+269 = 193+257 = 199+251 = 211+239 = 223+227 = 227+223 = 239+211 = 251+199 = 257+193 = 269+181 = 271+179 = 277+173 = 283+167 = 293+157 = 311+139 = 313+137 = 337+113 = 347+103 = 349+101 = 353+97 = 367+83 = 379+71 = 383+67 = 389+61 = 397+53 = 409+41 = 419+31 = 421+29 = 431+19 = 433+17 = 439+11 = 443+7 (# 54) 452 = 3+449 = 13+439 = 19+433 = 31+421 = 43+409 = 73+379 = 79+373 = 103+349 = 139+313 = 181+271 = 211+241 = 223+229 = 229+223 = 241+211 = 271+181 = 313+139 = 349+103 = 373+79 = 379+73 = 409+43 = 421+31 = 433+19 = 439+13 = 449+3 (# 24) 454 = 5+449 = 11+443 = 23+431 = 53+401 = 71+383 = 101+353 = 107+347 = 137+317 = 173+281 = 191+263 = 197+257 = 227+227 = 257+197 = 263+191 = 281+173 = 317+137 = 347+107 = 353+101 = 383+71 = 401+53 = 431+23 = 443+11 = 449+5 (# 23) 456 = 7+449 = 13+443 = 17+439 = 23+433 = 37+419 = 47+409 = 59+397 = 67+389 = 73+383 = 83+373 = 89+367 = 97+359 = 103+353 = 107+349 = 109+347 = 139+317 = 149+307 = 163+293 = 173+283 = 179+277 = 193+263 = 199+257 = 223+233 = 227+229 = 229+227 = 233+223 = 257+199 = 263+193 = 277+179 = 283+173 = 293+163 = 307+149 = 317+139 = 347+109 = 349+107 = 353+103 = 359+97 = 367+89 = 373+83 = 383+73 = 389+67 = 397+59 = 409+47 = 419+37 = 433+23 = 439+17 = 443+13 = 449+7 (# 48) 458 = 19+439 = 37+421 = 61+397 = 79+379 = 109+349 = 127+331 = 151+307 = 181+277 = 229+229 = 277+181 = 307+151 = 331+127 = 349+109 = 379+79 = 397+61 = 421+37 = 439+19 (# 17) 460 = 3+457 = 11+449 = 17+443 = 29+431 = 41+419 = 59+401 = 71+389 = 101+359 = 107+353 = 113+347 = 149+311 = 167+293 = 179+281 = 191+269 = 197+263 = 227+233 = 233+227 = 263+197 = 269+191 = 281+179 = 293+167 = 311+149 = 347+113 = 353+107 = 359+101 = 389+71 = 401+59 = 419+41 = 431+29 = 443+17 = 449+11 = 457+3 (# 32) 462 = 5+457 = 13+449 = 19+443 = 23+439 = 29+433 = 31+431 = 41+421 = 43+419 = 53+409 = 61+401 = 73+389 = 79+383 = 83+379 = 89+373 = 103+359 = 109+353 = 113+349 = 131+331 = 149+313 = 151+311 = 179+283 = 181+281 = 191+271 = 193+269 = 199+263 = 211+251 = 223+239 = 229+233 = 233+229 = 239+223 = 251+211 = 263+199 = 269+193 = 271+191 = 281+181 = 283+179 = 311+151 = 313+149 = 331+131 = 349+113 = 353+109 = 359+103 = 373+89 = 379+83 = 383+79 = 389+73 = 401+61 = 409+53 = 419+43 = 421+41 = 431+31 = 433+29 = 439+23 = 443+19 = 449+13 = 457+5 (# 56) 464 = 3+461 = 7+457 = 31+433 = 43+421 = 67+397 = 97+367 = 127+337 = 151+313 = 157+307 = 181+283 = 193+271 = 223+241 = 241+223 = 271+193 = 283+181 = 307+157 = 313+151 = 337+127 = 367+97 = 397+67 = 421+43 = 433+31 = 457+7 = 461+3 (# 24) 466 = 3+463 = 5+461 = 17+449 = 23+443 = 47+419 = 83+383 = 107+359 = 113+353 = 149+317 = 173+293 = 197+269 = 227+239 = 233+233 = 239+227 = 269+197 = 293+173 = 317+149 = 353+113 = 359+107 = 383+83 = 419+47 = 443+23 = 449+17 = 461+5 = 463+3 (# 25) 468 = 5+463 = 7+461 = 11+457 = 19+449 = 29+439 = 37+431 = 47+421 = 59+409 = 67+401 = 71+397 = 79+389 = 89+379 = 101+367 = 109+359 = 131+337 = 137+331 = 151+317 = 157+311 = 191+277 = 197+271 = 199+269 = 211+257 = 227+241 = 229+239 = 239+229 = 241+227 = 257+211 = 269+199 = 271+197 = 277+191 = 311+157 = 317+151 = 331+137 = 337+131 = 359+109 = 367+101 = 379+89 = 389+79 = 397+71 = 401+67 = 409+59 = 421+47 = 431+37 = 439+29 = 449+19 = 457+11 = 461+7 = 463+5 (# 48) 470 = 3+467 = 7+463 = 13+457 = 31+439 = 37+433 = 61+409 = 73+397 = 97+373 = 103+367 = 139+331 = 157+313 = 163+307 = 193+277 = 199+271 = 229+241 = 241+229 = 271+199 = 277+193 = 307+163 = 313+157 = 331+139 = 367+103 = 373+97 = 397+73 = 409+61 = 433+37 = 439+31 = 457+13 = 463+7 = 467+3 (# 30) 472 = 5+467 = 11+461 = 23+449 = 29+443 = 41+431 = 53+419 = 71+401 = 83+389 = 89+383 = 113+359 = 179+293 = 191+281 = 233+239 = 239+233 = 281+191 = 293+179 = 359+113 = 383+89 = 389+83 = 401+71 = 419+53 = 431+41 = 443+29 = 449+23 = 461+11 = 467+5 (# 26) 474 = 7+467 = 11+463 = 13+461 = 17+457 = 31+443 = 41+433 = 43+431 = 53+421 = 73+401 = 101+373 = 107+367 = 127+347 = 137+337 = 157+317 = 163+311 = 167+307 = 181+293 = 191+283 = 193+281 = 197+277 = 211+263 = 223+251 = 233+241 = 241+233 = 251+223 = 263+211 = 277+197 = 281+193 = 283+191 = 293+181 = 307+167 = 311+163 = 317+157 = 337+137 = 347+127 = 367+107 = 373+101 = 401+73 = 421+53 = 431+43 = 433+41 = 443+31 = 457+17 = 461+13 = 463+11 = 467+7 (# 46) 476 = 13+463 = 19+457 = 37+439 = 43+433 = 67+409 = 79+397 = 97+379 = 103+373 = 109+367 = 127+349 = 139+337 = 163+313 = 193+283 = 199+277 = 277+199 = 283+193 = 313+163 = 337+139 = 349+127 = 367+109 = 373+103 = 379+97 = 397+79 = 409+67 = 433+43 = 439+37 = 457+19 = 463+13 (# 28) 478 = 11+467 = 17+461 = 29+449 = 47+431 = 59+419 = 89+389 = 131+347 = 167+311 = 197+281 = 227+251 = 239+239 = 251+227 = 281+197 = 311+167 = 347+131 = 389+89 = 419+59 = 431+47 = 449+29 = 461+17 = 467+11 (# 21) 480 = 13+467 = 17+463 = 19+461 = 23+457 = 31+449 = 37+443 = 41+439 = 47+433 = 59+421 = 61+419 = 71+409 = 79+401 = 83+397 = 97+383 = 101+379 = 107+373 = 113+367 = 127+353 = 131+349 = 149+331 = 163+317 = 167+313 = 173+307 = 197+283 = 199+281 = 211+269 = 223+257 = 229+251 = 239+241 = 241+239 = 251+229 = 257+223 = 269+211 = 281+199 = 283+197 = 307+173 = 313+167 = 317+163 = 331+149 = 349+131 = 353+127 = 367+113 = 373+107 = 379+101 = 383+97 = 397+83 = 401+79 = 409+71 = 419+61 = 421+59 = 433+47 = 439+41 = 443+37 = 449+31 = 457+23 = 461+19 = 463+17 = 467+13 (# 58) 482 = 3+479 = 19+463 = 43+439 = 61+421 = 73+409 = 103+379 = 109+373 = 151+331 = 199+283 = 211+271 = 241+241 = 271+211 = 283+199 = 331+151 = 373+109 = 379+103 = 409+73 = 421+61 = 439+43 = 463+19 = 479+3 (# 21) 484 = 5+479 = 17+467 = 23+461 = 41+443 = 53+431 = 83+401 = 101+383 = 131+353 = 137+347 = 167+317 = 173+311 = 191+293 = 227+257 = 233+251 = 251+233 = 257+227 = 293+191 = 311+173 = 317+167 = 347+137 = 353+131 = 383+101 = 401+83 = 431+53 = 443+41 = 461+23 = 467+17 = 479+5 (# 28) 486 = 7+479 = 19+467 = 23+463 = 29+457 = 37+449 = 43+443 = 47+439 = 53+433 = 67+419 = 89+397 = 97+389 = 103+383 = 107+379 = 113+373 = 127+359 = 137+349 = 139+347 = 149+337 = 173+313 = 179+307 = 193+293 = 223+263 = 229+257 = 257+229 = 263+223 = 293+193 = 307+179 = 313+173 = 337+149 = 347+139 = 349+137 = 359+127 = 373+113 = 379+107 = 383+103 = 389+97 = 397+89 = 419+67 = 433+53 = 439+47 = 443+43 = 449+37 = 457+29 = 463+23 = 467+19 = 479+7 (# 46) 488 = 31+457 = 67+421 = 79+409 = 109+379 = 139+349 = 151+337 = 157+331 = 181+307 = 211+277 = 277+211 = 307+181 = 331+157 = 337+151 = 349+139 = 379+109 = 409+79 = 421+67 = 457+31 (# 18) 490 = 3+487 = 11+479 = 23+467 = 29+461 = 41+449 = 47+443 = 59+431 = 71+419 = 89+401 = 101+389 = 107+383 = 131+359 = 137+353 = 173+317 = 179+311 = 197+293 = 227+263 = 233+257 = 239+251 = 251+239 = 257+233 = 263+227 = 293+197 = 311+179 = 317+173 = 353+137 = 359+131 = 383+107 = 389+101 = 401+89 = 419+71 = 431+59 = 443+47 = 449+41 = 461+29 = 467+23 = 479+11 = 487+3 (# 38) 492 = 5+487 = 13+479 = 29+463 = 31+461 = 43+449 = 53+439 = 59+433 = 61+431 = 71+421 = 73+419 = 83+409 = 103+389 = 109+383 = 113+379 = 139+353 = 179+313 = 181+311 = 199+293 = 211+281 = 223+269 = 229+263 = 241+251 = 251+241 = 263+229 = 269+223 = 281+211 = 293+199 = 311+181 = 313+179 = 353+139 = 379+113 = 383+109 = 389+103 = 409+83 = 419+73 = 421+71 = 431+61 = 433+59 = 439+53 = 449+43 = 461+31 = 463+29 = 479+13 = 487+5 (# 44) 494 = 3+491 = 7+487 = 31+463 = 37+457 = 61+433 = 73+421 = 97+397 = 127+367 = 157+337 = 163+331 = 181+313 = 211+283 = 223+271 = 271+223 = 283+211 = 313+181 = 331+163 = 337+157 = 367+127 = 397+97 = 421+73 = 433+61 = 457+37 = 463+31 = 487+7 = 491+3 (# 26) 496 = 5+491 = 17+479 = 29+467 = 47+449 = 53+443 = 107+389 = 113+383 = 137+359 = 149+347 = 179+317 = 227+269 = 233+263 = 239+257 = 257+239 = 263+233 = 269+227 = 317+179 = 347+149 = 359+137 = 383+113 = 389+107 = 443+53 = 449+47 = 467+29 = 479+17 = 491+5 (# 26) 498 = 7+491 = 11+487 = 19+479 = 31+467 = 37+461 = 41+457 = 59+439 = 67+431 = 79+419 = 89+409 = 97+401 = 101+397 = 109+389 = 131+367 = 139+359 = 149+349 = 151+347 = 167+331 = 181+317 = 191+307 = 227+271 = 229+269 = 241+257 = 257+241 = 269+229 = 271+227 = 307+191 = 317+181 = 331+167 = 347+151 = 349+149 = 359+139 = 367+131 = 389+109 = 397+101 = 401+97 = 409+89 = 419+79 = 431+67 = 439+59 = 457+41 = 461+37 = 467+31 = 479+19 = 487+11 = 491+7 (# 46) 500 = 13+487 = 37+463 = 43+457 = 61+439 = 67+433 = 79+421 = 103+397 = 127+373 = 151+349 = 163+337 = 193+307 = 223+277 = 229+271 = 271+229 = 277+223 = 307+193 = 337+163 = 349+151 = 373+127 = 397+103 = 421+79 = 433+67 = 439+61 = 457+43 = 463+37 = 487+13 (# 26) 502 = 3+499 = 11+491 = 23+479 = 41+461 = 53+449 = 59+443 = 71+431 = 83+419 = 101+401 = 113+389 = 149+353 = 191+311 = 233+269 = 239+263 = 251+251 = 263+239 = 269+233 = 311+191 = 353+149 = 389+113 = 401+101 = 419+83 = 431+71 = 443+59 = 449+53 = 461+41 = 479+23 = 491+11 = 499+3 (# 29) 504 = 5+499 = 13+491 = 17+487 = 37+467 = 41+463 = 43+461 = 47+457 = 61+443 = 71+433 = 73+431 = 83+421 = 103+401 = 107+397 = 131+373 = 137+367 = 151+353 = 157+347 = 167+337 = 173+331 = 191+313 = 193+311 = 197+307 = 211+293 = 223+281 = 227+277 = 233+271 = 241+263 = 263+241 = 271+233 = 277+227 = 281+223 = 293+211 = 307+197 = 311+193 = 313+191 = 331+173 = 337+167 = 347+157 = 353+151 = 367+137 = 373+131 = 397+107 = 401+103 = 421+83 = 431+73 = 433+71 = 443+61 = 457+47 = 461+43 = 463+41 = 467+37 = 487+17 = 491+13 = 499+5 (# 54) 506 = 3+503 = 7+499 = 19+487 = 43+463 = 67+439 = 73+433 = 97+409 = 109+397 = 127+379 = 139+367 = 157+349 = 193+313 = 199+307 = 223+283 = 229+277 = 277+229 = 283+223 = 307+199 = 313+193 = 349+157 = 367+139 = 379+127 = 397+109 = 409+97 = 433+73 = 439+67 = 463+43 = 487+19 = 499+7 = 503+3 (# 30) 508 = 5+503 = 17+491 = 29+479 = 41+467 = 47+461 = 59+449 = 89+419 = 107+401 = 149+359 = 191+317 = 197+311 = 227+281 = 239+269 = 251+257 = 257+251 = 269+239 = 281+227 = 311+197 = 317+191 = 359+149 = 401+107 = 419+89 = 449+59 = 461+47 = 467+41 = 479+29 = 491+17 = 503+5 (# 28) 510 = 7+503 = 11+499 = 19+491 = 23+487 = 31+479 = 43+467 = 47+463 = 53+457 = 61+449 = 67+443 = 71+439 = 79+431 = 89+421 = 101+409 = 109+401 = 113+397 = 127+383 = 131+379 = 137+373 = 151+359 = 157+353 = 163+347 = 173+337 = 179+331 = 193+317 = 197+313 = 199+311 = 227+283 = 229+281 = 233+277 = 239+271 = 241+269 = 269+241 = 271+239 = 277+233 = 281+229 = 283+227 = 311+199 = 313+197 = 317+193 = 331+179 = 337+173 = 347+163 = 353+157 = 359+151 = 373+137 = 379+131 = 383+127 = 397+113 = 401+109 = 409+101 = 421+89 = 431+79 = 439+71 = 443+67 = 449+61 = 457+53 = 463+47 = 467+43 = 479+31 = 487+23 = 491+19 = 499+11 = 503+7 (# 64) 512 = 3+509 = 13+499 = 73+439 = 79+433 = 103+409 = 139+373 = 163+349 = 181+331 = 199+313 = 229+283 = 241+271 = 271+241 = 283+229 = 313+199 = 331+181 = 349+163 = 373+139 = 409+103 = 433+79 = 439+73 = 499+13 = 509+3 (# 22) 514 = 5+509 = 11+503 = 23+491 = 47+467 = 53+461 = 71+443 = 83+431 = 113+401 = 131+383 = 167+347 = 197+317 = 233+281 = 251+263 = 257+257 = 263+251 = 281+233 = 317+197 = 347+167 = 383+131 = 401+113 = 431+83 = 443+71 = 461+53 = 467+47 = 491+23 = 503+11 = 509+5 (# 27) 516 = 7+509 = 13+503 = 17+499 = 29+487 = 37+479 = 53+463 = 59+457 = 67+449 = 73+443 = 83+433 = 97+419 = 107+409 = 127+389 = 137+379 = 149+367 = 157+359 = 163+353 = 167+349 = 179+337 = 199+317 = 223+293 = 233+283 = 239+277 = 277+239 = 283+233 = 293+223 = 317+199 = 337+179 = 349+167 = 353+163 = 359+157 = 367+149 = 379+137 = 389+127 = 409+107 = 419+97 = 433+83 = 443+73 = 449+67 = 457+59 = 463+53 = 479+37 = 487+29 = 499+17 = 503+13 = 509+7 (# 46) 518 = 19+499 = 31+487 = 61+457 = 79+439 = 97+421 = 109+409 = 139+379 = 151+367 = 181+337 = 211+307 = 241+277 = 277+241 = 307+211 = 337+181 = 367+151 = 379+139 = 409+109 = 421+97 = 439+79 = 457+61 = 487+31 = 499+19 (# 22) 520 = 11+509 = 17+503 = 29+491 = 41+479 = 53+467 = 59+461 = 71+449 = 89+431 = 101+419 = 131+389 = 137+383 = 167+353 = 173+347 = 227+293 = 239+281 = 251+269 = 257+263 = 263+257 = 269+251 = 281+239 = 293+227 = 347+173 = 353+167 = 383+137 = 389+131 = 419+101 = 431+89 = 449+71 = 461+59 = 467+53 = 479+41 = 491+29 = 503+17 = 509+11 (# 34) 522 = 13+509 = 19+503 = 23+499 = 31+491 = 43+479 = 59+463 = 61+461 = 73+449 = 79+443 = 83+439 = 89+433 = 101+421 = 103+419 = 113+409 = 139+383 = 149+373 = 163+359 = 173+349 = 191+331 = 211+311 = 229+293 = 239+283 = 241+281 = 251+271 = 271+251 = 281+241 = 283+239 = 293+229 = 311+211 = 331+191 = 349+173 = 359+163 = 373+149 = 383+139 = 409+113 = 419+103 = 421+101 = 433+89 = 439+83 = 443+79 = 449+73 = 461+61 = 463+59 = 479+43 = 491+31 = 499+23 = 503+19 = 509+13 (# 48) 524 = 3+521 = 37+487 = 61+463 = 67+457 = 103+421 = 127+397 = 151+373 = 157+367 = 193+331 = 211+313 = 241+283 = 283+241 = 313+211 = 331+193 = 367+157 = 373+151 = 397+127 = 421+103 = 457+67 = 463+61 = 487+37 = 521+3 (# 22) 526 = 3+523 = 5+521 = 17+509 = 23+503 = 47+479 = 59+467 = 83+443 = 107+419 = 137+389 = 167+359 = 173+353 = 179+347 = 233+293 = 257+269 = 263+263 = 269+257 = 293+233 = 347+179 = 353+173 = 359+167 = 389+137 = 419+107 = 443+83 = 467+59 = 479+47 = 503+23 = 509+17 = 521+5 = 523+3 (# 29) 528 = 5+523 = 7+521 = 19+509 = 29+499 = 37+491 = 41+487 = 61+467 = 67+461 = 71+457 = 79+449 = 89+439 = 97+431 = 107+421 = 109+419 = 127+401 = 131+397 = 139+389 = 149+379 = 179+349 = 181+347 = 191+337 = 197+331 = 211+317 = 251+277 = 257+271 = 271+257 = 277+251 = 317+211 = 331+197 = 337+191 = 347+181 = 349+179 = 379+149 = 389+139 = 397+131 = 401+127 = 419+109 = 421+107 = 431+97 = 439+89 = 449+79 = 457+71 = 461+67 = 467+61 = 487+41 = 491+37 = 499+29 = 509+19 = 521+7 = 523+5 (# 50) 530 = 7+523 = 31+499 = 43+487 = 67+463 = 73+457 = 97+433 = 109+421 = 151+379 = 157+373 = 163+367 = 181+349 = 193+337 = 199+331 = 223+307 = 307+223 = 331+199 = 337+193 = 349+181 = 367+163 = 373+157 = 379+151 = 421+109 = 433+97 = 457+73 = 463+67 = 487+43 = 499+31 = 523+7 (# 28) 532 = 11+521 = 23+509 = 29+503 = 41+491 = 53+479 = 71+461 = 83+449 = 89+443 = 101+431 = 113+419 = 131+401 = 149+383 = 173+359 = 179+353 = 239+293 = 251+281 = 263+269 = 269+263 = 281+251 = 293+239 = 353+179 = 359+173 = 383+149 = 401+131 = 419+113 = 431+101 = 443+89 = 449+83 = 461+71 = 479+53 = 491+41 = 503+29 = 509+23 = 521+11 (# 34) 534 = 11+523 = 13+521 = 31+503 = 43+491 = 47+487 = 67+467 = 71+463 = 73+461 = 101+433 = 103+431 = 113+421 = 137+397 = 151+383 = 167+367 = 181+353 = 197+337 = 223+311 = 227+307 = 241+293 = 251+283 = 257+277 = 263+271 = 271+263 = 277+257 = 283+251 = 293+241 = 307+227 = 311+223 = 337+197 = 353+181 = 367+167 = 383+151 = 397+137 = 421+113 = 431+103 = 433+101 = 461+73 = 463+71 = 467+67 = 487+47 = 491+43 = 503+31 = 521+13 = 523+11 (# 44) 536 = 13+523 = 37+499 = 73+463 = 79+457 = 97+439 = 103+433 = 127+409 = 139+397 = 157+379 = 163+373 = 199+337 = 223+313 = 229+307 = 307+229 = 313+223 = 337+199 = 373+163 = 379+157 = 397+139 = 409+127 = 433+103 = 439+97 = 457+79 = 463+73 = 499+37 = 523+13 (# 26) 538 = 17+521 = 29+509 = 47+491 = 59+479 = 71+467 = 89+449 = 107+431 = 137+401 = 149+389 = 179+359 = 191+347 = 227+311 = 257+281 = 269+269 = 281+257 = 311+227 = 347+191 = 359+179 = 389+149 = 401+137 = 431+107 = 449+89 = 467+71 = 479+59 = 491+47 = 509+29 = 521+17 (# 27) 540 = 17+523 = 19+521 = 31+509 = 37+503 = 41+499 = 53+487 = 61+479 = 73+467 = 79+461 = 83+457 = 97+443 = 101+439 = 107+433 = 109+431 = 131+409 = 139+401 = 151+389 = 157+383 = 167+373 = 173+367 = 181+359 = 191+349 = 193+347 = 223+317 = 227+313 = 229+311 = 233+307 = 257+283 = 263+277 = 269+271 = 271+269 = 277+263 = 283+257 = 307+233 = 311+229 = 313+227 = 317+223 = 347+193 = 349+191 = 359+181 = 367+173 = 373+167 = 383+157 = 389+151 = 401+139 = 409+131 = 431+109 = 433+107 = 439+101 = 443+97 = 457+83 = 461+79 = 467+73 = 479+61 = 487+53 = 499+41 = 503+37 = 509+31 = 521+19 = 523+17 (# 60) 542 = 19+523 = 43+499 = 79+463 = 103+439 = 109+433 = 163+379 = 193+349 = 211+331 = 229+313 = 271+271 = 313+229 = 331+211 = 349+193 = 379+163 = 433+109 = 439+103 = 463+79 = 499+43 = 523+19 (# 19) 544 = 3+541 = 23+521 = 41+503 = 53+491 = 83+461 = 101+443 = 113+431 = 191+353 = 197+347 = 227+317 = 233+311 = 251+293 = 263+281 = 281+263 = 293+251 = 311+233 = 317+227 = 347+197 = 353+191 = 431+113 = 443+101 = 461+83 = 491+53 = 503+41 = 521+23 = 541+3 (# 26) 546 = 5+541 = 23+523 = 37+509 = 43+503 = 47+499 = 59+487 = 67+479 = 79+467 = 83+463 = 89+457 = 97+449 = 103+443 = 107+439 = 113+433 = 127+419 = 137+409 = 149+397 = 157+389 = 163+383 = 167+379 = 173+373 = 179+367 = 193+353 = 197+349 = 199+347 = 229+317 = 233+313 = 239+307 = 263+283 = 269+277 = 277+269 = 283+263 = 307+239 = 313+233 = 317+229 = 347+199 = 349+197 = 353+193 = 367+179 = 373+173 = 379+167 = 383+163 = 389+157 = 397+149 = 409+137 = 419+127 = 433+113 = 439+107 = 443+103 = 449+97 = 457+89 = 463+83 = 467+79 = 479+67 = 487+59 = 499+47 = 503+43 = 509+37 = 523+23 = 541+5 (# 60) 548 = 7+541 = 61+487 = 109+439 = 127+421 = 139+409 = 151+397 = 181+367 = 199+349 = 211+337 = 241+307 = 271+277 = 277+271 = 307+241 = 337+211 = 349+199 = 367+181 = 397+151 = 409+139 = 421+127 = 439+109 = 487+61 = 541+7 (# 22) 550 = 3+547 = 29+521 = 41+509 = 47+503 = 59+491 = 71+479 = 83+467 = 89+461 = 101+449 = 107+443 = 131+419 = 149+401 = 167+383 = 191+359 = 197+353 = 233+317 = 239+311 = 257+293 = 269+281 = 281+269 = 293+257 = 311+239 = 317+233 = 353+197 = 359+191 = 383+167 = 401+149 = 419+131 = 443+107 = 449+101 = 461+89 = 467+83 = 479+71 = 491+59 = 503+47 = 509+41 = 521+29 = 547+3 (# 38) 552 = 5+547 = 11+541 = 29+523 = 31+521 = 43+509 = 53+499 = 61+491 = 73+479 = 89+463 = 103+449 = 109+443 = 113+439 = 131+421 = 151+401 = 163+389 = 173+379 = 179+373 = 193+359 = 199+353 = 239+313 = 241+311 = 269+283 = 271+281 = 281+271 = 283+269 = 311+241 = 313+239 = 353+199 = 359+193 = 373+179 = 379+173 = 389+163 = 401+151 = 421+131 = 439+113 = 443+109 = 449+103 = 463+89 = 479+73 = 491+61 = 499+53 = 509+43 = 521+31 = 523+29 = 541+11 = 547+5 (# 46) 554 = 7+547 = 13+541 = 31+523 = 67+487 = 97+457 = 157+397 = 181+373 = 223+331 = 241+313 = 271+283 = 277+277 = 283+271 = 313+241 = 331+223 = 373+181 = 397+157 = 457+97 = 487+67 = 523+31 = 541+13 = 547+7 (# 21) 556 = 47+509 = 53+503 = 89+467 = 107+449 = 113+443 = 137+419 = 167+389 = 173+383 = 197+359 = 239+317 = 263+293 = 293+263 = 317+239 = 359+197 = 383+173 = 389+167 = 419+137 = 443+113 = 449+107 = 467+89 = 503+53 = 509+47 (# 22) 558 = 11+547 = 17+541 = 37+521 = 59+499 = 67+491 = 71+487 = 79+479 = 97+461 = 101+457 = 109+449 = 127+431 = 137+421 = 139+419 = 149+409 = 157+401 = 179+379 = 191+367 = 199+359 = 211+347 = 227+331 = 241+317 = 251+307 = 277+281 = 281+277 = 307+251 = 317+241 = 331+227 = 347+211 = 359+199 = 367+191 = 379+179 = 401+157 = 409+149 = 419+139 = 421+137 = 431+127 = 449+109 = 457+101 = 461+97 = 479+79 = 487+71 = 491+67 = 499+59 = 521+37 = 541+17 = 547+11 (# 46) 560 = 3+557 = 13+547 = 19+541 = 37+523 = 61+499 = 73+487 = 97+463 = 103+457 = 127+433 = 139+421 = 151+409 = 163+397 = 181+379 = 193+367 = 211+349 = 223+337 = 229+331 = 277+283 = 283+277 = 331+229 = 337+223 = 349+211 = 367+193 = 379+181 = 397+163 = 409+151 = 421+139 = 433+127 = 457+103 = 463+97 = 487+73 = 499+61 = 523+37 = 541+19 = 547+13 = 557+3 (# 36) 562 = 5+557 = 41+521 = 53+509 = 59+503 = 71+491 = 83+479 = 101+461 = 113+449 = 131+431 = 173+389 = 179+383 = 251+311 = 269+293 = 281+281 = 293+269 = 311+251 = 383+179 = 389+173 = 431+131 = 449+113 = 461+101 = 479+83 = 491+71 = 503+59 = 509+53 = 521+41 = 557+5 (# 27) 564 = 7+557 = 17+547 = 23+541 = 41+523 = 43+521 = 61+503 = 73+491 = 97+467 = 101+463 = 103+461 = 107+457 = 131+433 = 163+401 = 167+397 = 181+383 = 191+373 = 197+367 = 211+353 = 227+337 = 233+331 = 251+313 = 257+307 = 271+293 = 281+283 = 283+281 = 293+271 = 307+257 = 313+251 = 331+233 = 337+227 = 353+211 = 367+197 = 373+191 = 383+181 = 397+167 = 401+163 = 433+131 = 457+107 = 461+103 = 463+101 = 467+97 = 491+73 = 503+61 = 521+43 = 523+41 = 541+23 = 547+17 = 557+7 (# 48) 566 = 3+563 = 19+547 = 43+523 = 67+499 = 79+487 = 103+463 = 109+457 = 127+439 = 157+409 = 193+373 = 199+367 = 229+337 = 283+283 = 337+229 = 367+199 = 373+193 = 409+157 = 439+127 = 457+109 = 463+103 = 487+79 = 499+67 = 523+43 = 547+19 = 563+3 (# 25) 568 = 5+563 = 11+557 = 47+521 = 59+509 = 89+479 = 101+467 = 107+461 = 137+431 = 149+419 = 167+401 = 179+389 = 251+317 = 257+311 = 311+257 = 317+251 = 389+179 = 401+167 = 419+149 = 431+137 = 461+107 = 467+101 = 479+89 = 509+59 = 521+47 = 557+11 = 563+5 (# 26) 570 = 7+563 = 13+557 = 23+547 = 29+541 = 47+523 = 61+509 = 67+503 = 71+499 = 79+491 = 83+487 = 103+467 = 107+463 = 109+461 = 113+457 = 127+443 = 131+439 = 137+433 = 139+431 = 149+421 = 151+419 = 173+397 = 181+389 = 191+379 = 197+373 = 211+359 = 223+347 = 233+337 = 239+331 = 257+313 = 263+307 = 277+293 = 293+277 = 307+263 = 313+257 = 331+239 = 337+233 = 347+223 = 359+211 = 373+197 = 379+191 = 389+181 = 397+173 = 419+151 = 421+149 = 431+139 = 433+137 = 439+131 = 443+127 = 457+113 = 461+109 = 463+107 = 467+103 = 487+83 = 491+79 = 499+71 = 503+67 = 509+61 = 523+47 = 541+29 = 547+23 = 557+13 = 563+7 (# 62) 572 = 3+569 = 31+541 = 73+499 = 109+463 = 139+433 = 151+421 = 163+409 = 193+379 = 199+373 = 223+349 = 241+331 = 331+241 = 349+223 = 373+199 = 379+193 = 409+163 = 421+151 = 433+139 = 463+109 = 499+73 = 541+31 = 569+3 (# 22) 574 = 3+571 = 5+569 = 11+563 = 17+557 = 53+521 = 71+503 = 83+491 = 107+467 = 113+461 = 131+443 = 173+401 = 191+383 = 227+347 = 257+317 = 263+311 = 281+293 = 293+281 = 311+263 = 317+257 = 347+227 = 383+191 = 401+173 = 443+131 = 461+113 = 467+107 = 491+83 = 503+71 = 521+53 = 557+17 = 563+11 = 569+5 = 571+3 (# 32) 576 = 5+571 = 7+569 = 13+563 = 19+557 = 29+547 = 53+523 = 67+509 = 73+503 = 89+487 = 97+479 = 109+467 = 113+463 = 127+449 = 137+439 = 157+419 = 167+409 = 179+397 = 193+383 = 197+379 = 223+353 = 227+349 = 229+347 = 239+337 = 263+313 = 269+307 = 283+293 = 293+283 = 307+269 = 313+263 = 337+239 = 347+229 = 349+227 = 353+223 = 379+197 = 383+193 = 397+179 = 409+167 = 419+157 = 439+137 = 449+127 = 463+113 = 467+109 = 479+97 = 487+89 = 503+73 = 509+67 = 523+53 = 547+29 = 557+19 = 563+13 = 569+7 = 571+5 (# 52) 578 = 7+571 = 31+547 = 37+541 = 79+499 = 139+439 = 157+421 = 181+397 = 199+379 = 211+367 = 229+349 = 241+337 = 271+307 = 307+271 = 337+241 = 349+229 = 367+211 = 379+199 = 397+181 = 421+157 = 439+139 = 499+79 = 541+37 = 547+31 = 571+7 (# 24) 580 = 3+577 = 11+569 = 17+563 = 23+557 = 59+521 = 71+509 = 89+491 = 101+479 = 113+467 = 131+449 = 137+443 = 149+431 = 179+401 = 191+389 = 197+383 = 227+353 = 233+347 = 263+317 = 269+311 = 311+269 = 317+263 = 347+233 = 353+227 = 383+197 = 389+191 = 401+179 = 431+149 = 443+137 = 449+131 = 467+113 = 479+101 = 491+89 = 509+71 = 521+59 = 557+23 = 563+17 = 569+11 = 577+3 (# 38) 582 = 5+577 = 11+571 = 13+569 = 19+563 = 41+541 = 59+523 = 61+521 = 73+509 = 79+503 = 83+499 = 103+479 = 139+443 = 149+433 = 151+431 = 163+419 = 173+409 = 181+401 = 193+389 = 199+383 = 223+359 = 229+353 = 233+349 = 251+331 = 269+313 = 271+311 = 311+271 = 313+269 = 331+251 = 349+233 = 353+229 = 359+223 = 383+199 = 389+193 = 401+181 = 409+173 = 419+163 = 431+151 = 433+149 = 443+139 = 479+103 = 499+83 = 503+79 = 509+73 = 521+61 = 523+59 = 541+41 = 563+19 = 569+13 = 571+11 = 577+5 (# 50) 584 = 7+577 = 13+571 = 37+547 = 43+541 = 61+523 = 97+487 = 127+457 = 151+433 = 163+421 = 211+373 = 271+313 = 277+307 = 307+277 = 313+271 = 373+211 = 421+163 = 433+151 = 457+127 = 487+97 = 523+61 = 541+43 = 547+37 = 571+13 = 577+7 (# 24) 586 = 17+569 = 23+563 = 29+557 = 83+503 = 107+479 = 137+449 = 167+419 = 197+389 = 227+359 = 233+353 = 239+347 = 269+317 = 293+293 = 317+269 = 347+239 = 353+233 = 359+227 = 389+197 = 419+167 = 449+137 = 479+107 = 503+83 = 557+29 = 563+23 = 569+17 (# 25) 588 = 11+577 = 17+571 = 19+569 = 31+557 = 41+547 = 47+541 = 67+521 = 79+509 = 89+499 = 97+491 = 101+487 = 109+479 = 127+461 = 131+457 = 139+449 = 149+439 = 157+431 = 167+421 = 179+409 = 191+397 = 199+389 = 229+359 = 239+349 = 241+347 = 251+337 = 257+331 = 271+317 = 277+311 = 281+307 = 307+281 = 311+277 = 317+271 = 331+257 = 337+251 = 347+241 = 349+239 = 359+229 = 389+199 = 397+191 = 409+179 = 421+167 = 431+157 = 439+149 = 449+139 = 457+131 = 461+127 = 479+109 = 487+101 = 491+97 = 499+89 = 509+79 = 521+67 = 541+47 = 547+41 = 557+31 = 569+19 = 571+17 = 577+11 (# 58) 590 = 3+587 = 13+577 = 19+571 = 43+547 = 67+523 = 103+487 = 127+463 = 151+439 = 157+433 = 181+409 = 193+397 = 211+379 = 223+367 = 241+349 = 277+313 = 283+307 = 307+283 = 313+277 = 349+241 = 367+223 = 379+211 = 397+193 = 409+181 = 433+157 = 439+151 = 463+127 = 487+103 = 523+67 = 547+43 = 571+19 = 577+13 = 587+3 (# 32) 592 = 5+587 = 23+569 = 29+563 = 71+521 = 83+509 = 89+503 = 101+491 = 113+479 = 131+461 = 149+443 = 173+419 = 191+401 = 233+359 = 239+353 = 281+311 = 311+281 = 353+239 = 359+233 = 401+191 = 419+173 = 443+149 = 461+131 = 479+113 = 491+101 = 503+89 = 509+83 = 521+71 = 563+29 = 569+23 = 587+5 (# 30) 594 = 7+587 = 17+577 = 23+571 = 31+563 = 37+557 = 47+547 = 53+541 = 71+523 = 73+521 = 103+491 = 107+487 = 127+467 = 131+463 = 137+457 = 151+443 = 163+431 = 173+421 = 193+401 = 197+397 = 211+383 = 227+367 = 241+353 = 257+337 = 263+331 = 277+317 = 281+313 = 283+311 = 311+283 = 313+281 = 317+277 = 331+263 = 337+257 = 353+241 = 367+227 = 383+211 = 397+197 = 401+193 = 421+173 = 431+163 = 443+151 = 457+137 = 463+131 = 467+127 = 487+107 = 491+103 = 521+73 = 523+71 = 541+53 = 547+47 = 557+37 = 563+31 = 571+23 = 577+17 = 587+7 (# 54) 596 = 3+593 = 19+577 = 73+523 = 97+499 = 109+487 = 139+457 = 157+439 = 163+433 = 199+397 = 223+373 = 229+367 = 283+313 = 313+283 = 367+229 = 373+223 = 397+199 = 433+163 = 439+157 = 457+139 = 487+109 = 499+97 = 523+73 = 577+19 = 593+3 (# 24) 598 = 5+593 = 11+587 = 29+569 = 41+557 = 89+509 = 107+491 = 131+467 = 137+461 = 149+449 = 167+431 = 179+419 = 197+401 = 239+359 = 251+347 = 281+317 = 317+281 = 347+251 = 359+239 = 401+197 = 419+179 = 431+167 = 449+149 = 461+137 = 467+131 = 491+107 = 509+89 = 557+41 = 569+29 = 587+11 = 593+5 (# 30) 600 = 7+593 = 13+587 = 23+577 = 29+571 = 31+569 = 37+563 = 43+557 = 53+547 = 59+541 = 79+521 = 97+503 = 101+499 = 109+491 = 113+487 = 137+463 = 139+461 = 151+449 = 157+443 = 167+433 = 179+421 = 181+419 = 191+409 = 199+401 = 211+389 = 227+373 = 233+367 = 241+359 = 251+349 = 263+337 = 269+331 = 283+317 = 293+307 = 307+293 = 317+283 = 331+269 = 337+263 = 349+251 = 359+241 = 367+233 = 373+227 = 389+211 = 401+199 = 409+191 = 419+181 = 421+179 = 433+167 = 443+157 = 449+151 = 461+139 = 463+137 = 487+113 = 491+109 = 499+101 = 503+97 = 521+79 = 541+59 = 547+53 = 557+43 = 563+37 = 569+31 = 571+29 = 577+23 = 587+13 = 593+7 (# 64) 602 = 3+599 = 31+571 = 61+541 = 79+523 = 103+499 = 139+463 = 163+439 = 181+421 = 193+409 = 223+379 = 229+373 = 271+331 = 331+271 = 373+229 = 379+223 = 409+193 = 421+181 = 439+163 = 463+139 = 499+103 = 523+79 = 541+61 = 571+31 = 599+3 (# 24) 604 = 3+601 = 5+599 = 11+593 = 17+587 = 41+563 = 47+557 = 83+521 = 101+503 = 113+491 = 137+467 = 173+431 = 251+353 = 257+347 = 293+311 = 311+293 = 347+257 = 353+251 = 431+173 = 467+137 = 491+113 = 503+101 = 521+83 = 557+47 = 563+41 = 587+17 = 593+11 = 599+5 = 601+3 (# 28) 606 = 5+601 = 7+599 = 13+593 = 19+587 = 29+577 = 37+569 = 43+563 = 59+547 = 83+523 = 97+509 = 103+503 = 107+499 = 127+479 = 139+467 = 149+457 = 157+449 = 163+443 = 167+439 = 173+433 = 197+409 = 223+383 = 227+379 = 233+373 = 239+367 = 257+349 = 269+337 = 293+313 = 313+293 = 337+269 = 349+257 = 367+239 = 373+233 = 379+227 = 383+223 = 409+197 = 433+173 = 439+167 = 443+163 = 449+157 = 457+149 = 467+139 = 479+127 = 499+107 = 503+103 = 509+97 = 523+83 = 547+59 = 563+43 = 569+37 = 577+29 = 587+19 = 593+13 = 599+7 = 601+5 (# 54) 608 = 7+601 = 31+577 = 37+571 = 61+547 = 67+541 = 109+499 = 151+457 = 199+409 = 211+397 = 229+379 = 241+367 = 271+337 = 277+331 = 331+277 = 337+271 = 367+241 = 379+229 = 397+211 = 409+199 = 457+151 = 499+109 = 541+67 = 547+61 = 571+37 = 577+31 = 601+7 (# 26) 610 = 3+607 = 11+599 = 17+593 = 23+587 = 41+569 = 47+563 = 53+557 = 89+521 = 101+509 = 107+503 = 131+479 = 149+461 = 167+443 = 179+431 = 191+419 = 227+383 = 251+359 = 257+353 = 263+347 = 293+317 = 317+293 = 347+263 = 353+257 = 359+251 = 383+227 = 419+191 = 431+179 = 443+167 = 461+149 = 479+131 = 503+107 = 509+101 = 521+89 = 557+53 = 563+47 = 569+41 = 587+23 = 593+17 = 599+11 = 607+3 (# 40) 612 = 5+607 = 11+601 = 13+599 = 19+593 = 41+571 = 43+569 = 71+541 = 89+523 = 103+509 = 109+503 = 113+499 = 149+463 = 151+461 = 163+449 = 173+439 = 179+433 = 181+431 = 191+421 = 193+419 = 211+401 = 223+389 = 229+383 = 233+379 = 239+373 = 263+349 = 281+331 = 331+281 = 349+263 = 373+239 = 379+233 = 383+229 = 389+223 = 401+211 = 419+193 = 421+191 = 431+181 = 433+179 = 439+173 = 449+163 = 461+151 = 463+149 = 499+113 = 503+109 = 509+103 = 523+89 = 541+71 = 569+43 = 571+41 = 593+19 = 599+13 = 601+11 = 607+5 (# 52) 614 = 7+607 = 13+601 = 37+577 = 43+571 = 67+547 = 73+541 = 127+487 = 151+463 = 157+457 = 181+433 = 193+421 = 241+373 = 277+337 = 283+331 = 307+307 = 331+283 = 337+277 = 373+241 = 421+193 = 433+181 = 457+157 = 463+151 = 487+127 = 541+73 = 547+67 = 571+43 = 577+37 = 601+13 = 607+7 (# 29) 616 = 3+613 = 17+599 = 23+593 = 29+587 = 47+569 = 53+563 = 59+557 = 107+509 = 113+503 = 137+479 = 149+467 = 167+449 = 173+443 = 197+419 = 227+389 = 233+383 = 257+359 = 263+353 = 269+347 = 347+269 = 353+263 = 359+257 = 383+233 = 389+227 = 419+197 = 443+173 = 449+167 = 467+149 = 479+137 = 503+113 = 509+107 = 557+59 = 563+53 = 569+47 = 587+29 = 593+23 = 599+17 = 613+3 (# 38) 618 = 5+613 = 11+607 = 17+601 = 19+599 = 31+587 = 41+577 = 47+571 = 61+557 = 71+547 = 97+521 = 109+509 = 127+491 = 131+487 = 139+479 = 151+467 = 157+461 = 179+439 = 197+421 = 199+419 = 229+389 = 239+379 = 251+367 = 269+349 = 271+347 = 281+337 = 307+311 = 311+307 = 337+281 = 347+271 = 349+269 = 367+251 = 379+239 = 389+229 = 419+199 = 421+197 = 439+179 = 461+157 = 467+151 = 479+139 = 487+131 = 491+127 = 509+109 = 521+97 = 547+71 = 557+61 = 571+47 = 577+41 = 587+31 = 599+19 = 601+17 = 607+11 = 613+5 (# 52) 620 = 3+617 = 7+613 = 13+607 = 19+601 = 43+577 = 73+547 = 79+541 = 97+523 = 157+463 = 163+457 = 181+439 = 199+421 = 211+409 = 223+397 = 241+379 = 271+349 = 283+337 = 307+313 = 313+307 = 337+283 = 349+271 = 379+241 = 397+223 = 409+211 = 421+199 = 439+181 = 457+163 = 463+157 = 523+97 = 541+79 = 547+73 = 577+43 = 601+19 = 607+13 = 613+7 = 617+3 (# 36) 622 = 3+619 = 5+617 = 23+599 = 29+593 = 53+569 = 59+563 = 101+521 = 113+509 = 131+491 = 173+449 = 179+443 = 191+431 = 233+389 = 239+383 = 263+359 = 269+353 = 311+311 = 353+269 = 359+263 = 383+239 = 389+233 = 431+191 = 443+179 = 449+173 = 491+131 = 509+113 = 521+101 = 563+59 = 569+53 = 593+29 = 599+23 = 617+5 = 619+3 (# 33) 624 = 5+619 = 7+617 = 11+613 = 17+607 = 23+601 = 31+593 = 37+587 = 47+577 = 53+571 = 61+563 = 67+557 = 83+541 = 101+523 = 103+521 = 137+487 = 157+467 = 163+461 = 167+457 = 181+443 = 191+433 = 193+431 = 223+401 = 227+397 = 241+383 = 251+373 = 257+367 = 271+353 = 277+347 = 293+331 = 307+317 = 311+313 = 313+311 = 317+307 = 331+293 = 347+277 = 353+271 = 367+257 = 373+251 = 383+241 = 397+227 = 401+223 = 431+193 = 433+191 = 443+181 = 457+167 = 461+163 = 467+157 = 487+137 = 521+103 = 523+101 = 541+83 = 557+67 = 563+61 = 571+53 = 577+47 = 587+37 = 593+31 = 601+23 = 607+17 = 613+11 = 617+7 = 619+5 (# 62) 626 = 7+619 = 13+613 = 19+607 = 79+547 = 103+523 = 127+499 = 139+487 = 163+463 = 193+433 = 229+397 = 277+349 = 313+313 = 349+277 = 397+229 = 433+193 = 463+163 = 487+139 = 499+127 = 523+103 = 547+79 = 607+19 = 613+13 = 619+7 (# 23) 628 = 11+617 = 29+599 = 41+587 = 59+569 = 71+557 = 107+521 = 137+491 = 149+479 = 167+461 = 179+449 = 197+431 = 227+401 = 239+389 = 269+359 = 281+347 = 311+317 = 317+311 = 347+281 = 359+269 = 389+239 = 401+227 = 431+197 = 449+179 = 461+167 = 479+149 = 491+137 = 521+107 = 557+71 = 569+59 = 587+41 = 599+29 = 617+11 (# 32) 630 = 11+619 = 13+617 = 17+613 = 23+607 = 29+601 = 31+599 = 37+593 = 43+587 = 53+577 = 59+571 = 61+569 = 67+563 = 73+557 = 83+547 = 89+541 = 107+523 = 109+521 = 127+503 = 131+499 = 139+491 = 151+479 = 163+467 = 167+463 = 173+457 = 181+449 = 191+439 = 197+433 = 199+431 = 211+419 = 229+401 = 233+397 = 241+389 = 251+379 = 257+373 = 263+367 = 271+359 = 277+353 = 281+349 = 283+347 = 293+337 = 313+317 = 317+313 = 337+293 = 347+283 = 349+281 = 353+277 = 359+271 = 367+263 = 373+257 = 379+251 = 389+241 = 397+233 = 401+229 = 419+211 = 431+199 = 433+197 = 439+191 = 449+181 = 457+173 = 463+167 = 467+163 = 479+151 = 491+139 = 499+131 = 503+127 = 521+109 = 523+107 = 541+89 = 547+83 = 557+73 = 563+67 = 569+61 = 571+59 = 577+53 = 587+43 = 593+37 = 599+31 = 601+29 = 607+23 = 613+17 = 617+13 = 619+11 (# 82) 632 = 13+619 = 19+613 = 31+601 = 61+571 = 109+523 = 193+439 = 199+433 = 211+421 = 223+409 = 283+349 = 349+283 = 409+223 = 421+211 = 433+199 = 439+193 = 523+109 = 571+61 = 601+31 = 613+19 = 619+13 (# 20) 634 = 3+631 = 17+617 = 41+593 = 47+587 = 71+563 = 113+521 = 131+503 = 167+467 = 173+461 = 191+443 = 233+401 = 251+383 = 281+353 = 317+317 = 353+281 = 383+251 = 401+233 = 443+191 = 461+173 = 467+167 = 503+131 = 521+113 = 563+71 = 587+47 = 593+41 = 617+17 = 631+3 (# 27) 636 = 5+631 = 17+619 = 19+617 = 23+613 = 29+607 = 37+599 = 43+593 = 59+577 = 67+569 = 73+563 = 79+557 = 89+547 = 113+523 = 127+509 = 137+499 = 149+487 = 157+479 = 173+463 = 179+457 = 193+443 = 197+439 = 227+409 = 239+397 = 257+379 = 263+373 = 269+367 = 277+359 = 283+353 = 353+283 = 359+277 = 367+269 = 373+263 = 379+257 = 397+239 = 409+227 = 439+197 = 443+193 = 457+179 = 463+173 = 479+157 = 487+149 = 499+137 = 509+127 = 523+113 = 547+89 = 557+79 = 563+73 = 569+67 = 577+59 = 593+43 = 599+37 = 607+29 = 613+23 = 617+19 = 619+17 = 631+5 (# 56) 638 = 7+631 = 19+619 = 31+607 = 37+601 = 61+577 = 67+571 = 97+541 = 139+499 = 151+487 = 181+457 = 199+439 = 229+409 = 241+397 = 271+367 = 307+331 = 331+307 = 367+271 = 397+241 = 409+229 = 439+199 = 457+181 = 487+151 = 499+139 = 541+97 = 571+67 = 577+61 = 601+37 = 607+31 = 619+19 = 631+7 (# 30) 640 = 23+617 = 41+599 = 47+593 = 53+587 = 71+569 = 83+557 = 131+509 = 137+503 = 149+491 = 173+467 = 179+461 = 191+449 = 197+443 = 239+401 = 251+389 = 257+383 = 281+359 = 293+347 = 347+293 = 359+281 = 383+257 = 389+251 = 401+239 = 443+197 = 449+191 = 461+179 = 467+173 = 491+149 = 503+137 = 509+131 = 557+83 = 569+71 = 587+53 = 593+47 = 599+41 = 617+23 (# 36) 642 = 11+631 = 23+619 = 29+613 = 41+601 = 43+599 = 71+571 = 73+569 = 79+563 = 101+541 = 139+503 = 151+491 = 163+479 = 179+463 = 181+461 = 193+449 = 199+443 = 211+431 = 223+419 = 233+409 = 241+401 = 263+379 = 269+373 = 283+359 = 293+349 = 311+331 = 331+311 = 349+293 = 359+283 = 373+269 = 379+263 = 401+241 = 409+233 = 419+223 = 431+211 = 443+199 = 449+193 = 461+181 = 463+179 = 479+163 = 491+151 = 503+139 = 541+101 = 563+79 = 569+73 = 571+71 = 599+43 = 601+41 = 613+29 = 619+23 = 631+11 (# 50) 644 = 3+641 = 13+631 = 31+613 = 37+607 = 43+601 = 67+577 = 73+571 = 97+547 = 103+541 = 157+487 = 181+463 = 211+433 = 223+421 = 271+373 = 277+367 = 307+337 = 313+331 = 331+313 = 337+307 = 367+277 = 373+271 = 421+223 = 433+211 = 463+181 = 487+157 = 541+103 = 547+97 = 571+73 = 577+67 = 601+43 = 607+37 = 613+31 = 631+13 = 641+3 (# 34) 646 = 3+643 = 5+641 = 29+617 = 47+599 = 53+593 = 59+587 = 83+563 = 89+557 = 137+509 = 167+479 = 179+467 = 197+449 = 227+419 = 257+389 = 263+383 = 293+353 = 353+293 = 383+263 = 389+257 = 419+227 = 449+197 = 467+179 = 479+167 = 509+137 = 557+89 = 563+83 = 587+59 = 593+53 = 599+47 = 617+29 = 641+5 = 643+3 (# 32) 648 = 5+643 = 7+641 = 17+631 = 29+619 = 31+617 = 41+607 = 47+601 = 61+587 = 71+577 = 79+569 = 101+547 = 107+541 = 127+521 = 139+509 = 149+499 = 157+491 = 181+467 = 191+457 = 199+449 = 227+421 = 229+419 = 239+409 = 251+397 = 269+379 = 281+367 = 311+337 = 317+331 = 331+317 = 337+311 = 367+281 = 379+269 = 397+251 = 409+239 = 419+229 = 421+227 = 449+199 = 457+191 = 467+181 = 491+157 = 499+149 = 509+139 = 521+127 = 541+107 = 547+101 = 569+79 = 577+71 = 587+61 = 601+47 = 607+41 = 617+31 = 619+29 = 631+17 = 641+7 = 643+5 (# 54) 650 = 3+647 = 7+643 = 19+631 = 31+619 = 37+613 = 43+607 = 73+577 = 79+571 = 103+547 = 109+541 = 127+523 = 151+499 = 163+487 = 193+457 = 211+439 = 229+421 = 241+409 = 271+379 = 277+373 = 283+367 = 313+337 = 337+313 = 367+283 = 373+277 = 379+271 = 409+241 = 421+229 = 439+211 = 457+193 = 487+163 = 499+151 = 523+127 = 541+109 = 547+103 = 571+79 = 577+73 = 607+43 = 613+37 = 619+31 = 631+19 = 643+7 = 647+3 (# 42) 652 = 5+647 = 11+641 = 53+599 = 59+593 = 83+569 = 89+563 = 131+521 = 149+503 = 173+479 = 191+461 = 233+419 = 251+401 = 263+389 = 269+383 = 293+359 = 359+293 = 383+269 = 389+263 = 401+251 = 419+233 = 461+191 = 479+173 = 503+149 = 521+131 = 563+89 = 569+83 = 593+59 = 599+53 = 641+11 = 647+5 (# 30) 654 = 7+647 = 11+643 = 13+641 = 23+631 = 37+617 = 41+613 = 47+607 = 53+601 = 61+593 = 67+587 = 83+571 = 97+557 = 107+547 = 113+541 = 131+523 = 151+503 = 163+491 = 167+487 = 191+463 = 193+461 = 197+457 = 211+443 = 223+431 = 233+421 = 257+397 = 271+383 = 281+373 = 307+347 = 317+337 = 337+317 = 347+307 = 373+281 = 383+271 = 397+257 = 421+233 = 431+223 = 443+211 = 457+197 = 461+193 = 463+191 = 487+167 = 491+163 = 503+151 = 523+131 = 541+113 = 547+107 = 557+97 = 571+83 = 587+67 = 593+61 = 601+53 = 607+47 = 613+41 = 617+37 = 631+23 = 641+13 = 643+11 = 647+7 (# 58) 656 = 3+653 = 13+643 = 37+619 = 43+613 = 79+577 = 109+547 = 157+499 = 193+463 = 199+457 = 223+433 = 277+379 = 283+373 = 307+349 = 349+307 = 373+283 = 379+277 = 433+223 = 457+199 = 463+193 = 499+157 = 547+109 = 577+79 = 613+43 = 619+37 = 643+13 = 653+3 (# 26) 658 = 5+653 = 11+647 = 17+641 = 41+617 = 59+599 = 71+587 = 89+569 = 101+557 = 137+521 = 149+509 = 167+491 = 179+479 = 191+467 = 197+461 = 227+431 = 239+419 = 257+401 = 269+389 = 311+347 = 347+311 = 389+269 = 401+257 = 419+239 = 431+227 = 461+197 = 467+191 = 479+179 = 491+167 = 509+149 = 521+137 = 557+101 = 569+89 = 587+71 = 599+59 = 617+41 = 641+17 = 647+11 = 653+5 (# 38) 660 = 7+653 = 13+647 = 17+643 = 19+641 = 29+631 = 41+619 = 43+617 = 47+613 = 53+607 = 59+601 = 61+599 = 67+593 = 73+587 = 83+577 = 89+571 = 97+563 = 103+557 = 113+547 = 137+523 = 139+521 = 151+509 = 157+503 = 173+487 = 181+479 = 193+467 = 197+463 = 199+461 = 211+449 = 227+433 = 229+431 = 239+421 = 241+419 = 251+409 = 263+397 = 271+389 = 277+383 = 281+379 = 293+367 = 307+353 = 311+349 = 313+347 = 347+313 = 349+311 = 353+307 = 367+293 = 379+281 = 383+277 = 389+271 = 397+263 = 409+251 = 419+241 = 421+239 = 431+229 = 433+227 = 449+211 = 461+199 = 463+197 = 467+193 = 479+181 = 487+173 = 503+157 = 509+151 = 521+139 = 523+137 = 547+113 = 557+103 = 563+97 = 571+89 = 577+83 = 587+73 = 593+67 = 599+61 = 601+59 = 607+53 = 613+47 = 617+43 = 619+41 = 631+29 = 641+19 = 643+17 = 647+13 = 653+7 (# 82) 662 = 3+659 = 19+643 = 31+631 = 43+619 = 61+601 = 139+523 = 163+499 = 199+463 = 223+439 = 229+433 = 241+421 = 283+379 = 313+349 = 331+331 = 349+313 = 379+283 = 421+241 = 433+229 = 439+223 = 463+199 = 499+163 = 523+139 = 601+61 = 619+43 = 631+31 = 643+19 = 659+3 (# 27) 664 = 3+661 = 5+659 = 11+653 = 17+647 = 23+641 = 47+617 = 71+593 = 101+563 = 107+557 = 173+491 = 197+467 = 233+431 = 263+401 = 281+383 = 311+353 = 317+347 = 347+317 = 353+311 = 383+281 = 401+263 = 431+233 = 467+197 = 491+173 = 557+107 = 563+101 = 593+71 = 617+47 = 641+23 = 647+17 = 653+11 = 659+5 = 661+3 (# 32) 666 = 5+661 = 7+659 = 13+653 = 19+647 = 23+643 = 47+619 = 53+613 = 59+607 = 67+599 = 73+593 = 79+587 = 89+577 = 97+569 = 103+563 = 109+557 = 157+509 = 163+503 = 167+499 = 179+487 = 199+467 = 223+443 = 227+439 = 233+433 = 257+409 = 269+397 = 277+389 = 283+383 = 293+373 = 307+359 = 313+353 = 317+349 = 349+317 = 353+313 = 359+307 = 373+293 = 383+283 = 389+277 = 397+269 = 409+257 = 433+233 = 439+227 = 443+223 = 467+199 = 487+179 = 499+167 = 503+163 = 509+157 = 557+109 = 563+103 = 569+97 = 577+89 = 587+79 = 593+73 = 599+67 = 607+59 = 613+53 = 619+47 = 643+23 = 647+19 = 653+13 = 659+7 = 661+5 (# 62) 668 = 7+661 = 37+631 = 61+607 = 67+601 = 97+571 = 127+541 = 181+487 = 211+457 = 229+439 = 271+397 = 331+337 = 337+331 = 397+271 = 439+229 = 457+211 = 487+181 = 541+127 = 571+97 = 601+67 = 607+61 = 631+37 = 661+7 (# 22) 670 = 11+659 = 17+653 = 23+647 = 29+641 = 53+617 = 71+599 = 83+587 = 101+569 = 107+563 = 113+557 = 149+521 = 167+503 = 179+491 = 191+479 = 227+443 = 239+431 = 251+419 = 269+401 = 281+389 = 311+359 = 317+353 = 353+317 = 359+311 = 389+281 = 401+269 = 419+251 = 431+239 = 443+227 = 479+191 = 491+179 = 503+167 = 521+149 = 557+113 = 563+107 = 569+101 = 587+83 = 599+71 = 617+53 = 641+29 = 647+23 = 653+17 = 659+11 (# 42) 672 = 11+661 = 13+659 = 19+653 = 29+643 = 31+641 = 41+631 = 53+619 = 59+613 = 71+601 = 73+599 = 79+593 = 101+571 = 103+569 = 109+563 = 131+541 = 149+523 = 151+521 = 163+509 = 173+499 = 181+491 = 193+479 = 211+461 = 223+449 = 229+443 = 233+439 = 239+433 = 241+431 = 251+421 = 263+409 = 271+401 = 283+389 = 293+379 = 313+359 = 359+313 = 379+293 = 389+283 = 401+271 = 409+263 = 421+251 = 431+241 = 433+239 = 439+233 = 443+229 = 449+223 = 461+211 = 479+193 = 491+181 = 499+173 = 509+163 = 521+151 = 523+149 = 541+131 = 563+109 = 569+103 = 571+101 = 593+79 = 599+73 = 601+71 = 613+59 = 619+53 = 631+41 = 641+31 = 643+29 = 653+19 = 659+13 = 661+11 (# 66) 674 = 13+661 = 31+643 = 43+631 = 61+613 = 67+607 = 73+601 = 97+577 = 103+571 = 127+547 = 151+523 = 211+463 = 241+433 = 277+397 = 307+367 = 337+337 = 367+307 = 397+277 = 433+241 = 463+211 = 523+151 = 547+127 = 571+103 = 577+97 = 601+73 = 607+67 = 613+61 = 631+43 = 643+31 = 661+13 (# 29) 676 = 3+673 = 17+659 = 23+653 = 29+647 = 59+617 = 83+593 = 89+587 = 107+569 = 113+563 = 167+509 = 173+503 = 197+479 = 227+449 = 233+443 = 257+419 = 293+383 = 317+359 = 359+317 = 383+293 = 419+257 = 443+233 = 449+227 = 479+197 = 503+173 = 509+167 = 563+113 = 569+107 = 587+89 = 593+83 = 617+59 = 647+29 = 653+23 = 659+17 = 673+3 (# 34) 678 = 5+673 = 17+661 = 19+659 = 31+647 = 37+641 = 47+631 = 59+619 = 61+617 = 71+607 = 79+599 = 101+577 = 107+571 = 109+569 = 131+547 = 137+541 = 157+521 = 179+499 = 191+487 = 199+479 = 211+467 = 229+449 = 239+439 = 257+421 = 269+409 = 277+401 = 281+397 = 311+367 = 331+347 = 347+331 = 367+311 = 397+281 = 401+277 = 409+269 = 421+257 = 439+239 = 449+229 = 467+211 = 479+199 = 487+191 = 499+179 = 521+157 = 541+137 = 547+131 = 569+109 = 571+107 = 577+101 = 599+79 = 607+71 = 617+61 = 619+59 = 631+47 = 641+37 = 647+31 = 659+19 = 661+17 = 673+5 (# 56) 680 = 3+677 = 7+673 = 19+661 = 37+643 = 61+619 = 67+613 = 73+607 = 79+601 = 103+577 = 109+571 = 139+541 = 157+523 = 181+499 = 193+487 = 223+457 = 241+439 = 271+409 = 283+397 = 307+373 = 313+367 = 331+349 = 349+331 = 367+313 = 373+307 = 397+283 = 409+271 = 439+241 = 457+223 = 487+193 = 499+181 = 523+157 = 541+139 = 571+109 = 577+103 = 601+79 = 607+73 = 613+67 = 619+61 = 643+37 = 661+19 = 673+7 = 677+3 (# 42) 682 = 5+677 = 23+659 = 29+653 = 41+641 = 83+599 = 89+593 = 113+569 = 173+509 = 179+503 = 191+491 = 233+449 = 239+443 = 251+431 = 263+419 = 281+401 = 293+389 = 389+293 = 401+281 = 419+263 = 431+251 = 443+239 = 449+233 = 491+191 = 503+179 = 509+173 = 569+113 = 593+89 = 599+83 = 641+41 = 653+29 = 659+23 = 677+5 (# 32) 684 = 7+677 = 11+673 = 23+661 = 31+653 = 37+647 = 41+643 = 43+641 = 53+631 = 67+617 = 71+613 = 83+601 = 97+587 = 107+577 = 113+571 = 127+557 = 137+547 = 163+521 = 181+503 = 193+491 = 197+487 = 223+461 = 227+457 = 241+443 = 251+433 = 263+421 = 283+401 = 311+373 = 317+367 = 331+353 = 337+347 = 347+337 = 353+331 = 367+317 = 373+311 = 401+283 = 421+263 = 433+251 = 443+241 = 457+227 = 461+223 = 487+197 = 491+193 = 503+181 = 521+163 = 547+137 = 557+127 = 571+113 = 577+107 = 587+97 = 601+83 = 613+71 = 617+67 = 631+53 = 641+43 = 643+41 = 647+37 = 653+31 = 661+23 = 673+11 = 677+7 (# 60) 686 = 3+683 = 13+673 = 43+643 = 67+619 = 73+613 = 79+607 = 109+577 = 139+547 = 163+523 = 199+487 = 223+463 = 229+457 = 277+409 = 307+379 = 313+373 = 337+349 = 349+337 = 373+313 = 379+307 = 409+277 = 457+229 = 463+223 = 487+199 = 523+163 = 547+139 = 577+109 = 607+79 = 613+73 = 619+67 = 643+43 = 673+13 = 683+3 (# 32) 688 = 5+683 = 11+677 = 29+659 = 41+647 = 47+641 = 71+617 = 89+599 = 101+587 = 131+557 = 167+521 = 179+509 = 197+491 = 227+461 = 239+449 = 257+431 = 269+419 = 419+269 = 431+257 = 449+239 = 461+227 = 491+197 = 509+179 = 521+167 = 557+131 = 587+101 = 599+89 = 617+71 = 641+47 = 647+41 = 659+29 = 677+11 = 683+5 (# 32) 690 = 7+683 = 13+677 = 17+673 = 29+661 = 31+659 = 37+653 = 43+647 = 47+643 = 59+631 = 71+619 = 73+617 = 83+607 = 89+601 = 97+593 = 103+587 = 113+577 = 127+563 = 149+541 = 167+523 = 181+509 = 191+499 = 199+491 = 211+479 = 223+467 = 227+463 = 229+461 = 233+457 = 241+449 = 251+439 = 257+433 = 269+421 = 271+419 = 281+409 = 293+397 = 307+383 = 311+379 = 317+373 = 331+359 = 337+353 = 353+337 = 359+331 = 373+317 = 379+311 = 383+307 = 397+293 = 409+281 = 419+271 = 421+269 = 433+257 = 439+251 = 449+241 = 457+233 = 461+229 = 463+227 = 467+223 = 479+211 = 491+199 = 499+191 = 509+181 = 523+167 = 541+149 = 563+127 = 577+113 = 587+103 = 593+97 = 601+89 = 607+83 = 617+73 = 619+71 = 631+59 = 643+47 = 647+43 = 653+37 = 659+31 = 661+29 = 673+17 = 677+13 = 683+7 (# 78) 692 = 19+673 = 31+661 = 61+631 = 73+619 = 79+613 = 151+541 = 193+499 = 229+463 = 271+421 = 283+409 = 313+379 = 379+313 = 409+283 = 421+271 = 463+229 = 499+193 = 541+151 = 613+79 = 619+73 = 631+61 = 661+31 = 673+19 (# 22) 694 = 3+691 = 11+683 = 17+677 = 41+653 = 47+647 = 53+641 = 101+593 = 107+587 = 131+563 = 137+557 = 173+521 = 191+503 = 227+467 = 233+461 = 251+443 = 263+431 = 293+401 = 311+383 = 347+347 = 383+311 = 401+293 = 431+263 = 443+251 = 461+233 = 467+227 = 503+191 = 521+173 = 557+137 = 563+131 = 587+107 = 593+101 = 641+53 = 647+47 = 653+41 = 677+17 = 683+11 = 691+3 (# 37) 696 = 5+691 = 13+683 = 19+677 = 23+673 = 37+659 = 43+653 = 53+643 = 79+617 = 83+613 = 89+607 = 97+599 = 103+593 = 109+587 = 127+569 = 139+557 = 149+547 = 173+523 = 193+503 = 197+499 = 229+467 = 233+463 = 239+457 = 257+439 = 263+433 = 277+419 = 307+389 = 313+383 = 317+379 = 337+359 = 347+349 = 349+347 = 359+337 = 379+317 = 383+313 = 389+307 = 419+277 = 433+263 = 439+257 = 457+239 = 463+233 = 467+229 = 499+197 = 503+193 = 523+173 = 547+149 = 557+139 = 569+127 = 587+109 = 593+103 = 599+97 = 607+89 = 613+83 = 617+79 = 643+53 = 653+43 = 659+37 = 673+23 = 677+19 = 683+13 = 691+5 (# 60) 698 = 7+691 = 37+661 = 67+631 = 79+619 = 97+601 = 127+571 = 151+547 = 157+541 = 199+499 = 211+487 = 241+457 = 277+421 = 331+367 = 349+349 = 367+331 = 421+277 = 457+241 = 487+211 = 499+199 = 541+157 = 547+151 = 571+127 = 601+97 = 619+79 = 631+67 = 661+37 = 691+7 (# 27) 700 = 17+683 = 23+677 = 41+659 = 47+653 = 53+647 = 59+641 = 83+617 = 101+599 = 107+593 = 113+587 = 131+569 = 137+563 = 179+521 = 191+509 = 197+503 = 233+467 = 239+461 = 251+449 = 257+443 = 269+431 = 281+419 = 311+389 = 317+383 = 347+353 = 353+347 = 383+317 = 389+311 = 419+281 = 431+269 = 443+257 = 449+251 = 461+239 = 467+233 = 503+197 = 509+191 = 521+179 = 563+137 = 569+131 = 587+113 = 593+107 = 599+101 = 617+83 = 641+59 = 647+53 = 653+47 = 659+41 = 677+23 = 683+17 (# 48) 702 = 11+691 = 19+683 = 29+673 = 41+661 = 43+659 = 59+643 = 61+641 = 71+631 = 83+619 = 89+613 = 101+601 = 103+599 = 109+593 = 131+571 = 139+563 = 179+523 = 181+521 = 193+509 = 199+503 = 211+491 = 223+479 = 239+463 = 241+461 = 263+439 = 269+433 = 271+431 = 281+421 = 283+419 = 293+409 = 313+389 = 349+353 = 353+349 = 389+313 = 409+293 = 419+283 = 421+281 = 431+271 = 433+269 = 439+263 = 461+241 = 463+239 = 479+223 = 491+211 = 503+199 = 509+193 = 521+181 = 523+179 = 563+139 = 571+131 = 593+109 = 599+103 = 601+101 = 613+89 = 619+83 = 631+71 = 641+61 = 643+59 = 659+43 = 661+41 = 673+29 = 683+19 = 691+11 (# 62) 704 = 3+701 = 13+691 = 31+673 = 43+661 = 61+643 = 73+631 = 97+607 = 103+601 = 127+577 = 157+547 = 163+541 = 181+523 = 241+463 = 271+433 = 283+421 = 307+397 = 331+373 = 337+367 = 367+337 = 373+331 = 397+307 = 421+283 = 433+271 = 463+241 = 523+181 = 541+163 = 547+157 = 577+127 = 601+103 = 607+97 = 631+73 = 643+61 = 661+43 = 673+31 = 691+13 = 701+3 (# 36) 706 = 5+701 = 23+683 = 29+677 = 47+659 = 53+653 = 59+647 = 89+617 = 107+599 = 113+593 = 137+569 = 149+557 = 197+509 = 227+479 = 239+467 = 257+449 = 263+443 = 317+389 = 347+359 = 353+353 = 359+347 = 389+317 = 443+263 = 449+257 = 467+239 = 479+227 = 509+197 = 557+149 = 569+137 = 593+113 = 599+107 = 617+89 = 647+59 = 653+53 = 659+47 = 677+29 = 683+23 = 701+5 (# 37) 708 = 7+701 = 17+691 = 31+677 = 47+661 = 61+647 = 67+641 = 89+619 = 101+607 = 107+601 = 109+599 = 131+577 = 137+571 = 139+569 = 151+557 = 167+541 = 199+509 = 229+479 = 241+467 = 251+457 = 269+439 = 277+431 = 307+401 = 311+397 = 349+359 = 359+349 = 397+311 = 401+307 = 431+277 = 439+269 = 457+251 = 467+241 = 479+229 = 509+199 = 541+167 = 557+151 = 569+139 = 571+137 = 577+131 = 599+109 = 601+107 = 607+101 = 619+89 = 641+67 = 647+61 = 661+47 = 677+31 = 691+17 = 701+7 (# 48) 710 = 19+691 = 37+673 = 67+643 = 79+631 = 97+613 = 103+607 = 109+601 = 139+571 = 163+547 = 211+499 = 223+487 = 271+439 = 277+433 = 313+397 = 331+379 = 337+373 = 373+337 = 379+331 = 397+313 = 433+277 = 439+271 = 487+223 = 499+211 = 547+163 = 571+139 = 601+109 = 607+103 = 613+97 = 631+79 = 643+67 = 673+37 = 691+19 (# 32) 712 = 3+709 = 11+701 = 29+683 = 53+659 = 59+653 = 71+641 = 113+599 = 149+563 = 191+521 = 233+479 = 251+461 = 263+449 = 269+443 = 281+431 = 293+419 = 311+401 = 353+359 = 359+353 = 401+311 = 419+293 = 431+281 = 443+269 = 449+263 = 461+251 = 479+233 = 521+191 = 563+149 = 599+113 = 641+71 = 653+59 = 659+53 = 683+29 = 701+11 = 709+3 (# 34) 714 = 5+709 = 13+701 = 23+691 = 31+683 = 37+677 = 41+673 = 53+661 = 61+653 = 67+647 = 71+643 = 73+641 = 83+631 = 97+617 = 101+613 = 107+607 = 113+601 = 127+587 = 137+577 = 151+563 = 157+557 = 167+547 = 173+541 = 191+523 = 193+521 = 211+503 = 223+491 = 227+487 = 251+463 = 257+457 = 271+443 = 281+433 = 283+431 = 293+421 = 313+401 = 317+397 = 331+383 = 347+367 = 367+347 = 383+331 = 397+317 = 401+313 = 421+293 = 431+283 = 433+281 = 443+271 = 457+257 = 463+251 = 487+227 = 491+223 = 503+211 = 521+193 = 523+191 = 541+173 = 547+167 = 557+157 = 563+151 = 577+137 = 587+127 = 601+113 = 607+107 = 613+101 = 617+97 = 631+83 = 641+73 = 643+71 = 647+67 = 653+61 = 661+53 = 673+41 = 677+37 = 683+31 = 691+23 = 701+13 = 709+5 (# 74) 716 = 7+709 = 43+673 = 73+643 = 97+619 = 103+613 = 109+607 = 139+577 = 193+523 = 229+487 = 277+439 = 283+433 = 307+409 = 337+379 = 349+367 = 367+349 = 379+337 = 409+307 = 433+283 = 439+277 = 487+229 = 523+193 = 577+139 = 607+109 = 613+103 = 619+97 = 643+73 = 673+43 = 709+7 (# 28) 718 = 17+701 = 41+677 = 59+659 = 71+647 = 101+617 = 131+587 = 149+569 = 197+521 = 227+491 = 239+479 = 251+467 = 257+461 = 269+449 = 317+401 = 359+359 = 401+317 = 449+269 = 461+257 = 467+251 = 479+239 = 491+227 = 521+197 = 569+149 = 587+131 = 617+101 = 647+71 = 659+59 = 677+41 = 701+17 (# 29) 720 = 11+709 = 19+701 = 29+691 = 37+683 = 43+677 = 47+673 = 59+661 = 61+659 = 67+653 = 73+647 = 79+641 = 89+631 = 101+619 = 103+617 = 107+613 = 113+607 = 127+593 = 149+571 = 151+569 = 157+563 = 163+557 = 173+547 = 179+541 = 197+523 = 199+521 = 211+509 = 229+491 = 233+487 = 241+479 = 257+463 = 263+457 = 271+449 = 277+443 = 281+439 = 311+409 = 331+389 = 337+383 = 347+373 = 353+367 = 367+353 = 373+347 = 383+337 = 389+331 = 409+311 = 439+281 = 443+277 = 449+271 = 457+263 = 463+257 = 479+241 = 487+233 = 491+229 = 509+211 = 521+199 = 523+197 = 541+179 = 547+173 = 557+163 = 563+157 = 569+151 = 571+149 = 593+127 = 607+113 = 613+107 = 617+103 = 619+101 = 631+89 = 641+79 = 647+73 = 653+67 = 659+61 = 661+59 = 673+47 = 677+43 = 683+37 = 691+29 = 701+19 = 709+11 (# 78) 722 = 3+719 = 13+709 = 31+691 = 61+661 = 79+643 = 103+619 = 109+613 = 151+571 = 181+541 = 199+523 = 223+499 = 283+439 = 313+409 = 349+373 = 373+349 = 409+313 = 439+283 = 499+223 = 523+199 = 541+181 = 571+151 = 613+109 = 619+103 = 643+79 = 661+61 = 691+31 = 709+13 = 719+3 (# 28) 724 = 5+719 = 23+701 = 41+683 = 47+677 = 71+653 = 83+641 = 107+617 = 131+593 = 137+587 = 167+557 = 233+491 = 257+467 = 263+461 = 281+443 = 293+431 = 431+293 = 443+281 = 461+263 = 467+257 = 491+233 = 557+167 = 587+137 = 593+131 = 617+107 = 641+83 = 653+71 = 677+47 = 683+41 = 701+23 = 719+5 (# 30) 726 = 7+719 = 17+709 = 43+683 = 53+673 = 67+659 = 73+653 = 79+647 = 83+643 = 107+619 = 109+617 = 113+613 = 127+599 = 139+587 = 149+577 = 157+569 = 163+563 = 179+547 = 223+503 = 227+499 = 239+487 = 263+463 = 269+457 = 277+449 = 283+443 = 293+433 = 307+419 = 317+409 = 337+389 = 347+379 = 353+373 = 359+367 = 367+359 = 373+353 = 379+347 = 389+337 = 409+317 = 419+307 = 433+293 = 443+283 = 449+277 = 457+269 = 463+263 = 487+239 = 499+227 = 503+223 = 547+179 = 563+163 = 569+157 = 577+149 = 587+139 = 599+127 = 613+113 = 617+109 = 619+107 = 643+83 = 647+79 = 653+73 = 659+67 = 673+53 = 683+43 = 709+17 = 719+7 (# 62) 728 = 19+709 = 37+691 = 67+661 = 97+631 = 109+619 = 127+601 = 151+577 = 157+571 = 181+547 = 229+499 = 241+487 = 271+457 = 307+421 = 331+397 = 349+379 = 379+349 = 397+331 = 421+307 = 457+271 = 487+241 = 499+229 = 547+181 = 571+157 = 577+151 = 601+127 = 619+109 = 631+97 = 661+67 = 691+37 = 709+19 (# 30) 730 = 3+727 = 11+719 = 29+701 = 47+683 = 53+677 = 71+659 = 83+647 = 89+641 = 113+617 = 131+599 = 137+593 = 167+563 = 173+557 = 227+503 = 239+491 = 251+479 = 263+467 = 269+461 = 281+449 = 311+419 = 347+383 = 383+347 = 419+311 = 449+281 = 461+269 = 467+263 = 479+251 = 491+239 = 503+227 = 557+173 = 563+167 = 593+137 = 599+131 = 617+113 = 641+89 = 647+83 = 659+71 = 677+53 = 683+47 = 701+29 = 719+11 = 727+3 (# 42) 732 = 5+727 = 13+719 = 23+709 = 31+701 = 41+691 = 59+673 = 71+661 = 73+659 = 79+653 = 89+643 = 101+631 = 113+619 = 131+601 = 139+593 = 163+569 = 191+541 = 211+521 = 223+509 = 229+503 = 233+499 = 241+491 = 269+463 = 271+461 = 283+449 = 293+439 = 311+421 = 313+419 = 331+401 = 349+383 = 353+379 = 359+373 = 373+359 = 379+353 = 383+349 = 401+331 = 419+313 = 421+311 = 439+293 = 449+283 = 461+271 = 463+269 = 491+241 = 499+233 = 503+229 = 509+223 = 521+211 = 541+191 = 569+163 = 593+139 = 601+131 = 619+113 = 631+101 = 643+89 = 653+79 = 659+73 = 661+71 = 673+59 = 691+41 = 701+31 = 709+23 = 719+13 = 727+5 (# 62) 734 = 7+727 = 43+691 = 61+673 = 73+661 = 103+631 = 127+607 = 157+577 = 163+571 = 193+541 = 211+523 = 271+463 = 277+457 = 313+421 = 337+397 = 367+367 = 397+337 = 421+313 = 457+277 = 463+271 = 523+211 = 541+193 = 571+163 = 577+157 = 607+127 = 631+103 = 661+73 = 673+61 = 691+43 = 727+7 (# 29) 736 = 3+733 = 17+719 = 53+683 = 59+677 = 83+653 = 89+647 = 137+599 = 149+587 = 167+569 = 173+563 = 179+557 = 227+509 = 233+503 = 257+479 = 269+467 = 293+443 = 317+419 = 347+389 = 353+383 = 383+353 = 389+347 = 419+317 = 443+293 = 467+269 = 479+257 = 503+233 = 509+227 = 557+179 = 563+173 = 569+167 = 587+149 = 599+137 = 647+89 = 653+83 = 677+59 = 683+53 = 719+17 = 733+3 (# 38) 738 = 5+733 = 11+727 = 19+719 = 29+709 = 37+701 = 47+691 = 61+677 = 79+659 = 97+641 = 107+631 = 131+607 = 137+601 = 139+599 = 151+587 = 167+571 = 181+557 = 191+547 = 197+541 = 229+509 = 239+499 = 251+487 = 271+467 = 277+461 = 281+457 = 307+431 = 317+421 = 337+401 = 349+389 = 359+379 = 379+359 = 389+349 = 401+337 = 421+317 = 431+307 = 457+281 = 461+277 = 467+271 = 487+251 = 499+239 = 509+229 = 541+197 = 547+191 = 557+181 = 571+167 = 587+151 = 599+139 = 601+137 = 607+131 = 631+107 = 641+97 = 659+79 = 677+61 = 691+47 = 701+37 = 709+29 = 719+19 = 727+11 = 733+5 (# 58) 740 = 7+733 = 13+727 = 31+709 = 67+673 = 79+661 = 97+643 = 109+631 = 127+613 = 139+601 = 163+577 = 193+547 = 199+541 = 241+499 = 277+463 = 283+457 = 307+433 = 331+409 = 367+373 = 373+367 = 409+331 = 433+307 = 457+283 = 463+277 = 499+241 = 541+199 = 547+193 = 577+163 = 601+139 = 613+127 = 631+109 = 643+97 = 661+79 = 673+67 = 709+31 = 727+13 = 733+7 (# 36) 742 = 3+739 = 23+719 = 41+701 = 59+683 = 83+659 = 89+653 = 101+641 = 149+593 = 173+569 = 179+563 = 233+509 = 239+503 = 251+491 = 263+479 = 281+461 = 293+449 = 311+431 = 353+389 = 359+383 = 383+359 = 389+353 = 431+311 = 449+293 = 461+281 = 479+263 = 491+251 = 503+239 = 509+233 = 563+179 = 569+173 = 593+149 = 641+101 = 653+89 = 659+83 = 683+59 = 701+41 = 719+23 = 739+3 (# 38) 744 = 5+739 = 11+733 = 17+727 = 43+701 = 53+691 = 61+683 = 67+677 = 71+673 = 83+661 = 97+647 = 101+643 = 103+641 = 113+631 = 127+617 = 131+613 = 137+607 = 151+593 = 157+587 = 167+577 = 173+571 = 181+563 = 197+547 = 223+521 = 241+503 = 257+487 = 277+467 = 281+463 = 283+461 = 311+433 = 313+431 = 347+397 = 397+347 = 431+313 = 433+311 = 461+283 = 463+281 = 467+277 = 487+257 = 503+241 = 521+223 = 547+197 = 563+181 = 571+173 = 577+167 = 587+157 = 593+151 = 607+137 = 613+131 = 617+127 = 631+113 = 641+103 = 643+101 = 647+97 = 661+83 = 673+71 = 677+67 = 683+61 = 691+53 = 701+43 = 727+17 = 733+11 = 739+5 (# 62) 746 = 3+743 = 7+739 = 13+733 = 19+727 = 37+709 = 73+673 = 103+643 = 127+619 = 139+607 = 199+547 = 223+523 = 283+463 = 307+439 = 313+433 = 337+409 = 349+397 = 367+379 = 373+373 = 379+367 = 397+349 = 409+337 = 433+313 = 439+307 = 463+283 = 523+223 = 547+199 = 607+139 = 619+127 = 643+103 = 673+73 = 709+37 = 727+19 = 733+13 = 739+7 = 743+3 (# 35) 748 = 5+743 = 29+719 = 47+701 = 71+677 = 89+659 = 101+647 = 107+641 = 131+617 = 149+599 = 179+569 = 191+557 = 227+521 = 239+509 = 257+491 = 269+479 = 281+467 = 317+431 = 347+401 = 359+389 = 389+359 = 401+347 = 431+317 = 467+281 = 479+269 = 491+257 = 509+239 = 521+227 = 557+191 = 569+179 = 599+149 = 617+131 = 641+107 = 647+101 = 659+89 = 677+71 = 701+47 = 719+29 = 743+5 (# 38) 750 = 7+743 = 11+739 = 17+733 = 23+727 = 31+719 = 41+709 = 59+691 = 67+683 = 73+677 = 89+661 = 97+653 = 103+647 = 107+643 = 109+641 = 131+619 = 137+613 = 149+601 = 151+599 = 157+593 = 163+587 = 173+577 = 179+571 = 181+569 = 193+557 = 227+523 = 229+521 = 241+509 = 251+499 = 263+487 = 271+479 = 283+467 = 293+457 = 307+443 = 311+439 = 317+433 = 331+419 = 349+401 = 353+397 = 367+383 = 383+367 = 397+353 = 401+349 = 419+331 = 433+317 = 439+311 = 443+307 = 457+293 = 467+283 = 479+271 = 487+263 = 499+251 = 509+241 = 521+229 = 523+227 = 557+193 = 569+181 = 571+179 = 577+173 = 587+163 = 593+157 = 599+151 = 601+149 = 613+137 = 619+131 = 641+109 = 643+107 = 647+103 = 653+97 = 661+89 = 677+73 = 683+67 = 691+59 = 709+41 = 719+31 = 727+23 = 733+17 = 739+11 = 743+7 (# 78) 752 = 13+739 = 19+733 = 43+709 = 61+691 = 79+673 = 109+643 = 139+613 = 151+601 = 181+571 = 211+541 = 229+523 = 313+439 = 331+421 = 373+379 = 379+373 = 421+331 = 439+313 = 523+229 = 541+211 = 571+181 = 601+151 = 613+139 = 643+109 = 673+79 = 691+61 = 709+43 = 733+19 = 739+13 (# 28) 754 = 3+751 = 11+743 = 53+701 = 71+683 = 101+653 = 107+647 = 113+641 = 137+617 = 167+587 = 191+563 = 197+557 = 233+521 = 251+503 = 263+491 = 293+461 = 311+443 = 353+401 = 401+353 = 443+311 = 461+293 = 491+263 = 503+251 = 521+233 = 557+197 = 563+191 = 587+167 = 617+137 = 641+113 = 647+107 = 653+101 = 683+71 = 701+53 = 743+11 = 751+3 (# 34) 756 = 5+751 = 13+743 = 17+739 = 23+733 = 29+727 = 37+719 = 47+709 = 73+683 = 79+677 = 83+673 = 97+659 = 103+653 = 109+647 = 113+643 = 137+619 = 139+617 = 149+607 = 157+599 = 163+593 = 179+577 = 193+563 = 199+557 = 233+523 = 257+499 = 269+487 = 277+479 = 293+463 = 307+449 = 313+443 = 317+439 = 337+419 = 347+409 = 359+397 = 367+389 = 373+383 = 383+373 = 389+367 = 397+359 = 409+347 = 419+337 = 439+317 = 443+313 = 449+307 = 463+293 = 479+277 = 487+269 = 499+257 = 523+233 = 557+199 = 563+193 = 577+179 = 593+163 = 599+157 = 607+149 = 617+139 = 619+137 = 643+113 = 647+109 = 653+103 = 659+97 = 673+83 = 677+79 = 683+73 = 709+47 = 719+37 = 727+29 = 733+23 = 739+17 = 743+13 = 751+5 (# 70) 758 = 7+751 = 19+739 = 31+727 = 67+691 = 97+661 = 127+631 = 139+619 = 151+607 = 157+601 = 181+577 = 211+547 = 271+487 = 337+421 = 349+409 = 379+379 = 409+349 = 421+337 = 487+271 = 547+211 = 577+181 = 601+157 = 607+151 = 619+139 = 631+127 = 661+97 = 691+67 = 727+31 = 739+19 = 751+7 (# 29) 760 = 3+757 = 17+743 = 41+719 = 59+701 = 83+677 = 101+659 = 107+653 = 113+647 = 167+593 = 173+587 = 191+569 = 197+563 = 239+521 = 251+509 = 257+503 = 269+491 = 281+479 = 293+467 = 311+449 = 317+443 = 359+401 = 401+359 = 443+317 = 449+311 = 467+293 = 479+281 = 491+269 = 503+257 = 509+251 = 521+239 = 563+197 = 569+191 = 587+173 = 593+167 = 647+113 = 653+107 = 659+101 = 677+83 = 701+59 = 719+41 = 743+17 = 757+3 (# 42) 762 = 5+757 = 11+751 = 19+743 = 23+739 = 29+733 = 43+719 = 53+709 = 61+701 = 71+691 = 79+683 = 89+673 = 101+661 = 103+659 = 109+653 = 131+631 = 149+613 = 163+599 = 191+571 = 193+569 = 199+563 = 239+523 = 241+521 = 263+499 = 271+491 = 283+479 = 313+449 = 331+431 = 353+409 = 373+389 = 379+383 = 383+379 = 389+373 = 409+353 = 431+331 = 449+313 = 479+283 = 491+271 = 499+263 = 521+241 = 523+239 = 563+199 = 569+193 = 571+191 = 599+163 = 613+149 = 631+131 = 653+109 = 659+103 = 661+101 = 673+89 = 683+79 = 691+71 = 701+61 = 709+53 = 719+43 = 733+29 = 739+23 = 743+19 = 751+11 = 757+5 (# 60) 764 = 3+761 = 7+757 = 13+751 = 31+733 = 37+727 = 73+691 = 103+661 = 151+613 = 157+607 = 163+601 = 193+571 = 223+541 = 241+523 = 277+487 = 307+457 = 331+433 = 367+397 = 397+367 = 433+331 = 457+307 = 487+277 = 523+241 = 541+223 = 571+193 = 601+163 = 607+157 = 613+151 = 661+103 = 691+73 = 727+37 = 733+31 = 751+13 = 757+7 = 761+3 (# 34) 766 = 5+761 = 23+743 = 47+719 = 83+683 = 89+677 = 107+659 = 113+653 = 149+617 = 167+599 = 173+593 = 179+587 = 197+569 = 257+509 = 263+503 = 317+449 = 347+419 = 383+383 = 419+347 = 449+317 = 503+263 = 509+257 = 569+197 = 587+179 = 593+173 = 599+167 = 617+149 = 653+113 = 659+107 = 677+89 = 683+83 = 719+47 = 743+23 = 761+5 (# 33) 768 = 7+761 = 11+757 = 17+751 = 29+739 = 41+727 = 59+709 = 67+701 = 107+661 = 109+659 = 127+641 = 137+631 = 149+619 = 151+617 = 167+601 = 181+587 = 191+577 = 197+571 = 199+569 = 211+557 = 227+541 = 269+499 = 277+491 = 281+487 = 307+461 = 311+457 = 337+431 = 347+421 = 349+419 = 359+409 = 367+401 = 379+389 = 389+379 = 401+367 = 409+359 = 419+349 = 421+347 = 431+337 = 457+311 = 461+307 = 487+281 = 491+277 = 499+269 = 541+227 = 557+211 = 569+199 = 571+197 = 577+191 = 587+181 = 601+167 = 617+151 = 619+149 = 631+137 = 641+127 = 659+109 = 661+107 = 701+67 = 709+59 = 727+41 = 739+29 = 751+17 = 757+11 = 761+7 (# 62) 770 = 13+757 = 19+751 = 31+739 = 37+733 = 43+727 = 61+709 = 79+691 = 97+673 = 109+661 = 127+643 = 139+631 = 151+619 = 157+613 = 163+607 = 193+577 = 199+571 = 223+547 = 229+541 = 271+499 = 283+487 = 307+463 = 313+457 = 331+439 = 337+433 = 349+421 = 373+397 = 397+373 = 421+349 = 433+337 = 439+331 = 457+313 = 463+307 = 487+283 = 499+271 = 541+229 = 547+223 = 571+199 = 577+193 = 607+163 = 613+157 = 619+151 = 631+139 = 643+127 = 661+109 = 673+97 = 691+79 = 709+61 = 727+43 = 733+37 = 739+31 = 751+19 = 757+13 (# 52) 772 = 3+769 = 11+761 = 29+743 = 53+719 = 71+701 = 89+683 = 113+659 = 131+641 = 173+599 = 179+593 = 251+521 = 263+509 = 269+503 = 281+491 = 293+479 = 311+461 = 353+419 = 383+389 = 389+383 = 419+353 = 461+311 = 479+293 = 491+281 = 503+269 = 509+263 = 521+251 = 593+179 = 599+173 = 641+131 = 659+113 = 683+89 = 701+71 = 719+53 = 743+29 = 761+11 = 769+3 (# 36) 774 = 5+769 = 13+761 = 17+757 = 23+751 = 31+743 = 41+733 = 47+727 = 73+701 = 83+691 = 97+677 = 101+673 = 113+661 = 127+647 = 131+643 = 157+617 = 167+607 = 173+601 = 181+593 = 197+577 = 211+563 = 227+547 = 233+541 = 251+523 = 271+503 = 283+491 = 307+467 = 311+463 = 313+461 = 317+457 = 331+443 = 353+421 = 373+401 = 401+373 = 421+353 = 443+331 = 457+317 = 461+313 = 463+311 = 467+307 = 491+283 = 503+271 = 523+251 = 541+233 = 547+227 = 563+211 = 577+197 = 593+181 = 601+173 = 607+167 = 617+157 = 643+131 = 647+127 = 661+113 = 673+101 = 677+97 = 691+83 = 701+73 = 727+47 = 733+41 = 743+31 = 751+23 = 757+17 = 761+13 = 769+5 (# 64) 776 = 3+773 = 7+769 = 19+757 = 37+739 = 43+733 = 67+709 = 103+673 = 157+619 = 163+613 = 199+577 = 229+547 = 277+499 = 313+463 = 337+439 = 367+409 = 379+397 = 397+379 = 409+367 = 439+337 = 463+313 = 499+277 = 547+229 = 577+199 = 613+163 = 619+157 = 673+103 = 709+67 = 733+43 = 739+37 = 757+19 = 769+7 = 773+3 (# 32) 778 = 5+773 = 17+761 = 59+719 = 101+677 = 131+647 = 137+641 = 179+599 = 191+587 = 257+521 = 269+509 = 311+467 = 317+461 = 347+431 = 359+419 = 389+389 = 419+359 = 431+347 = 461+317 = 467+311 = 509+269 = 521+257 = 587+191 = 599+179 = 641+137 = 647+131 = 677+101 = 719+59 = 761+17 = 773+5 (# 29) 780 = 7+773 = 11+769 = 19+761 = 23+757 = 29+751 = 37+743 = 41+739 = 47+733 = 53+727 = 61+719 = 71+709 = 79+701 = 89+691 = 97+683 = 103+677 = 107+673 = 127+653 = 137+643 = 139+641 = 149+631 = 163+617 = 167+613 = 173+607 = 179+601 = 181+599 = 193+587 = 211+569 = 223+557 = 233+547 = 239+541 = 257+523 = 271+509 = 277+503 = 281+499 = 293+487 = 313+467 = 317+463 = 331+449 = 337+443 = 347+433 = 349+431 = 359+421 = 379+401 = 383+397 = 397+383 = 401+379 = 421+359 = 431+349 = 433+347 = 443+337 = 449+331 = 463+317 = 467+313 = 487+293 = 499+281 = 503+277 = 509+271 = 523+257 = 541+239 = 547+233 = 557+223 = 569+211 = 587+193 = 599+181 = 601+179 = 607+173 = 613+167 = 617+163 = 631+149 = 641+139 = 643+137 = 653+127 = 673+107 = 677+103 = 683+97 = 691+89 = 701+79 = 709+71 = 719+61 = 727+53 = 733+47 = 739+41 = 743+37 = 751+29 = 757+23 = 761+19 = 769+11 = 773+7 (# 88) 782 = 13+769 = 31+751 = 43+739 = 73+709 = 109+673 = 139+643 = 151+631 = 163+619 = 181+601 = 211+571 = 241+541 = 283+499 = 349+433 = 373+409 = 409+373 = 433+349 = 499+283 = 541+241 = 571+211 = 601+181 = 619+163 = 631+151 = 643+139 = 673+109 = 709+73 = 739+43 = 751+31 = 769+13 (# 28) 784 = 11+773 = 23+761 = 41+743 = 83+701 = 101+683 = 107+677 = 131+653 = 137+647 = 167+617 = 191+593 = 197+587 = 227+557 = 263+521 = 281+503 = 293+491 = 317+467 = 353+431 = 383+401 = 401+383 = 431+353 = 467+317 = 491+293 = 503+281 = 521+263 = 557+227 = 587+197 = 593+191 = 617+167 = 647+137 = 653+131 = 677+107 = 683+101 = 701+83 = 743+41 = 761+23 = 773+11 (# 36) 786 = 13+773 = 17+769 = 29+757 = 43+743 = 47+739 = 53+733 = 59+727 = 67+719 = 103+683 = 109+677 = 113+673 = 127+659 = 139+647 = 167+619 = 173+613 = 179+607 = 193+593 = 199+587 = 223+563 = 229+557 = 239+547 = 263+523 = 277+509 = 283+503 = 307+479 = 337+449 = 347+439 = 353+433 = 367+419 = 389+397 = 397+389 = 419+367 = 433+353 = 439+347 = 449+337 = 479+307 = 503+283 = 509+277 = 523+263 = 547+239 = 557+229 = 563+223 = 587+199 = 593+193 = 607+179 = 613+173 = 619+167 = 647+139 = 659+127 = 673+113 = 677+109 = 683+103 = 719+67 = 727+59 = 733+53 = 739+47 = 743+43 = 757+29 = 769+17 = 773+13 (# 60) 788 = 19+769 = 31+757 = 37+751 = 61+727 = 79+709 = 97+691 = 127+661 = 157+631 = 181+607 = 211+577 = 241+547 = 331+457 = 349+439 = 367+421 = 379+409 = 409+379 = 421+367 = 439+349 = 457+331 = 547+241 = 577+211 = 607+181 = 631+157 = 661+127 = 691+97 = 709+79 = 727+61 = 751+37 = 757+31 = 769+19 (# 30) 790 = 3+787 = 17+773 = 29+761 = 47+743 = 71+719 = 89+701 = 107+683 = 113+677 = 131+659 = 137+653 = 149+641 = 173+617 = 191+599 = 197+593 = 227+563 = 233+557 = 269+521 = 281+509 = 311+479 = 347+443 = 359+431 = 389+401 = 401+389 = 431+359 = 443+347 = 479+311 = 509+281 = 521+269 = 557+233 = 563+227 = 593+197 = 599+191 = 617+173 = 641+149 = 653+137 = 659+131 = 677+113 = 683+107 = 701+89 = 719+71 = 743+47 = 761+29 = 773+17 = 787+3 (# 44) 792 = 5+787 = 19+773 = 23+769 = 31+761 = 41+751 = 53+739 = 59+733 = 73+719 = 83+709 = 101+691 = 109+683 = 131+661 = 139+653 = 149+643 = 151+641 = 173+619 = 179+613 = 191+601 = 193+599 = 199+593 = 223+569 = 229+563 = 251+541 = 269+523 = 271+521 = 283+509 = 293+499 = 313+479 = 331+461 = 349+443 = 353+439 = 359+433 = 373+419 = 383+409 = 409+383 = 419+373 = 433+359 = 439+353 = 443+349 = 461+331 = 479+313 = 499+293 = 509+283 = 521+271 = 523+269 = 541+251 = 563+229 = 569+223 = 593+199 = 599+193 = 601+191 = 613+179 = 619+173 = 641+151 = 643+149 = 653+139 = 661+131 = 683+109 = 691+101 = 709+83 = 719+73 = 733+59 = 739+53 = 751+41 = 761+31 = 769+23 = 773+19 = 787+5 (# 68) 794 = 7+787 = 37+757 = 43+751 = 61+733 = 67+727 = 103+691 = 151+643 = 163+631 = 181+613 = 193+601 = 223+571 = 271+523 = 307+487 = 331+463 = 337+457 = 373+421 = 397+397 = 421+373 = 457+337 = 463+331 = 487+307 = 523+271 = 571+223 = 601+193 = 613+181 = 631+163 = 643+151 = 691+103 = 727+67 = 733+61 = 751+43 = 757+37 = 787+7 (# 33) 796 = 23+773 = 53+743 = 113+683 = 137+659 = 149+647 = 179+617 = 197+599 = 227+569 = 233+563 = 239+557 = 293+503 = 317+479 = 347+449 = 353+443 = 443+353 = 449+347 = 479+317 = 503+293 = 557+239 = 563+233 = 569+227 = 599+197 = 617+179 = 647+149 = 659+137 = 683+113 = 743+53 = 773+23 (# 28) 798 = 11+787 = 29+769 = 37+761 = 41+757 = 47+751 = 59+739 = 71+727 = 79+719 = 89+709 = 97+701 = 107+691 = 137+661 = 139+659 = 151+647 = 157+641 = 167+631 = 179+619 = 181+617 = 191+607 = 197+601 = 199+599 = 211+587 = 227+571 = 229+569 = 241+557 = 251+547 = 257+541 = 277+521 = 307+491 = 311+487 = 331+467 = 337+461 = 349+449 = 359+439 = 367+431 = 379+419 = 389+409 = 397+401 = 401+397 = 409+389 = 419+379 = 431+367 = 439+359 = 449+349 = 461+337 = 467+331 = 487+311 = 491+307 = 521+277 = 541+257 = 547+251 = 557+241 = 569+229 = 571+227 = 587+211 = 599+199 = 601+197 = 607+191 = 617+181 = 619+179 = 631+167 = 641+157 = 647+151 = 659+139 = 661+137 = 691+107 = 701+97 = 709+89 = 719+79 = 727+71 = 739+59 = 751+47 = 757+41 = 761+37 = 769+29 = 787+11 (# 76) 800 = 3+797 = 13+787 = 31+769 = 43+757 = 61+739 = 67+733 = 73+727 = 109+691 = 127+673 = 139+661 = 157+643 = 181+619 = 193+607 = 199+601 = 223+577 = 229+571 = 277+523 = 313+487 = 337+463 = 367+433 = 379+421 = 421+379 = 433+367 = 463+337 = 487+313 = 523+277 = 571+229 = 577+223 = 601+199 = 607+193 = 619+181 = 643+157 = 661+139 = 673+127 = 691+109 = 727+73 = 733+67 = 739+61 = 757+43 = 769+31 = 787+13 = 797+3 (# 42) 802 = 5+797 = 29+773 = 41+761 = 59+743 = 83+719 = 101+701 = 149+653 = 233+569 = 239+563 = 281+521 = 293+509 = 311+491 = 353+449 = 359+443 = 383+419 = 401+401 = 419+383 = 443+359 = 449+353 = 491+311 = 509+293 = 521+281 = 563+239 = 569+233 = 653+149 = 701+101 = 719+83 = 743+59 = 761+41 = 773+29 = 797+5 (# 31) 804 = 7+797 = 17+787 = 31+773 = 43+761 = 47+757 = 53+751 = 61+743 = 71+733 = 103+701 = 113+691 = 127+677 = 131+673 = 151+653 = 157+647 = 163+641 = 173+631 = 191+613 = 197+607 = 211+593 = 227+577 = 233+571 = 241+563 = 257+547 = 263+541 = 281+523 = 283+521 = 313+491 = 317+487 = 337+467 = 347+457 = 373+431 = 383+421 = 421+383 = 431+373 = 457+347 = 467+337 = 487+317 = 491+313 = 521+283 = 523+281 = 541+263 = 547+257 = 563+241 = 571+233 = 577+227 = 593+211 = 607+197 = 613+191 = 631+173 = 641+163 = 647+157 = 653+151 = 673+131 = 677+127 = 691+113 = 701+103 = 733+71 = 743+61 = 751+53 = 757+47 = 761+43 = 773+31 = 787+17 = 797+7 (# 64) 806 = 19+787 = 37+769 = 67+739 = 73+733 = 79+727 = 97+709 = 163+643 = 193+613 = 199+607 = 229+577 = 283+523 = 307+499 = 349+457 = 367+439 = 373+433 = 397+409 = 409+397 = 433+373 = 439+367 = 457+349 = 499+307 = 523+283 = 577+229 = 607+199 = 613+193 = 643+163 = 709+97 = 727+79 = 733+73 = 739+67 = 769+37 = 787+19 (# 32) 808 = 11+797 = 47+761 = 89+719 = 107+701 = 131+677 = 149+659 = 167+641 = 191+617 = 239+569 = 251+557 = 317+491 = 347+461 = 359+449 = 389+419 = 419+389 = 449+359 = 461+347 = 491+317 = 557+251 = 569+239 = 617+191 = 641+167 = 659+149 = 677+131 = 701+107 = 719+89 = 761+47 = 797+11 (# 28) 810 = 13+797 = 23+787 = 37+773 = 41+769 = 53+757 = 59+751 = 67+743 = 71+739 = 83+727 = 101+709 = 109+701 = 127+683 = 137+673 = 149+661 = 151+659 = 157+653 = 163+647 = 167+643 = 179+631 = 191+619 = 193+617 = 197+613 = 211+599 = 223+587 = 233+577 = 239+571 = 241+569 = 263+547 = 269+541 = 307+503 = 311+499 = 331+479 = 347+463 = 349+461 = 353+457 = 367+443 = 379+431 = 389+421 = 401+409 = 409+401 = 421+389 = 431+379 = 443+367 = 457+353 = 461+349 = 463+347 = 479+331 = 499+311 = 503+307 = 541+269 = 547+263 = 569+241 = 571+239 = 577+233 = 587+223 = 599+211 = 613+197 = 617+193 = 619+191 = 631+179 = 643+167 = 647+163 = 653+157 = 659+151 = 661+149 = 673+137 = 683+127 = 701+109 = 709+101 = 727+83 = 739+71 = 743+67 = 751+59 = 757+53 = 769+41 = 773+37 = 787+23 = 797+13 (# 78) 812 = 3+809 = 43+769 = 61+751 = 73+739 = 79+733 = 103+709 = 139+673 = 151+661 = 181+631 = 193+619 = 199+613 = 211+601 = 241+571 = 271+541 = 313+499 = 349+463 = 373+439 = 379+433 = 433+379 = 439+373 = 463+349 = 499+313 = 541+271 = 571+241 = 601+211 = 613+199 = 619+193 = 631+181 = 661+151 = 673+139 = 709+103 = 733+79 = 739+73 = 751+61 = 769+43 = 809+3 (# 36) 814 = 3+811 = 5+809 = 17+797 = 41+773 = 53+761 = 71+743 = 113+701 = 131+683 = 137+677 = 167+647 = 173+641 = 197+617 = 227+587 = 251+563 = 257+557 = 293+521 = 311+503 = 347+467 = 353+461 = 383+431 = 431+383 = 461+353 = 467+347 = 503+311 = 521+293 = 557+257 = 563+251 = 587+227 = 617+197 = 641+173 = 647+167 = 677+137 = 683+131 = 701+113 = 743+71 = 761+53 = 773+41 = 797+17 = 809+5 = 811+3 (# 40) 816 = 5+811 = 7+809 = 19+797 = 29+787 = 43+773 = 47+769 = 59+757 = 73+743 = 83+733 = 89+727 = 97+719 = 107+709 = 139+677 = 157+659 = 163+653 = 173+643 = 197+619 = 199+617 = 223+593 = 229+587 = 239+577 = 269+547 = 293+523 = 307+509 = 313+503 = 317+499 = 337+479 = 349+467 = 353+463 = 359+457 = 367+449 = 373+443 = 383+433 = 397+419 = 419+397 = 433+383 = 443+373 = 449+367 = 457+359 = 463+353 = 467+349 = 479+337 = 499+317 = 503+313 = 509+307 = 523+293 = 547+269 = 577+239 = 587+229 = 593+223 = 617+199 = 619+197 = 643+173 = 653+163 = 659+157 = 677+139 = 709+107 = 719+97 = 727+89 = 733+83 = 743+73 = 757+59 = 769+47 = 773+43 = 787+29 = 797+19 = 809+7 = 811+5 (# 68) 818 = 7+811 = 31+787 = 61+757 = 67+751 = 79+739 = 109+709 = 127+691 = 157+661 = 199+619 = 211+607 = 241+577 = 271+547 = 277+541 = 331+487 = 379+439 = 397+421 = 409+409 = 421+397 = 439+379 = 487+331 = 541+277 = 547+271 = 577+241 = 607+211 = 619+199 = 661+157 = 691+127 = 709+109 = 739+79 = 751+67 = 757+61 = 787+31 = 811+7 (# 33) 820 = 11+809 = 23+797 = 47+773 = 59+761 = 101+719 = 137+683 = 167+653 = 173+647 = 179+641 = 227+593 = 233+587 = 251+569 = 257+563 = 263+557 = 311+509 = 317+503 = 353+467 = 359+461 = 389+431 = 401+419 = 419+401 = 431+389 = 461+359 = 467+353 = 503+317 = 509+311 = 557+263 = 563+257 = 569+251 = 587+233 = 593+227 = 641+179 = 647+173 = 653+167 = 683+137 = 719+101 = 761+59 = 773+47 = 797+23 = 809+11 (# 40) 822 = 11+811 = 13+809 = 53+769 = 61+761 = 71+751 = 79+743 = 83+739 = 89+733 = 103+719 = 113+709 = 131+691 = 139+683 = 149+673 = 163+659 = 179+643 = 181+641 = 191+631 = 223+599 = 229+593 = 251+571 = 281+541 = 313+509 = 331+491 = 359+463 = 373+449 = 379+443 = 383+439 = 389+433 = 401+421 = 421+401 = 433+389 = 439+383 = 443+379 = 449+373 = 463+359 = 491+331 = 509+313 = 541+281 = 571+251 = 593+229 = 599+223 = 631+191 = 641+181 = 643+179 = 659+163 = 673+149 = 683+139 = 691+131 = 709+113 = 719+103 = 733+89 = 739+83 = 743+79 = 751+71 = 761+61 = 769+53 = 809+13 = 811+11 (# 58) 824 = 3+821 = 13+811 = 37+787 = 67+757 = 73+751 = 97+727 = 151+673 = 163+661 = 181+643 = 193+631 = 211+613 = 223+601 = 277+547 = 283+541 = 337+487 = 367+457 = 457+367 = 487+337 = 541+283 = 547+277 = 601+223 = 613+211 = 631+193 = 643+181 = 661+163 = 673+151 = 727+97 = 751+73 = 757+67 = 787+37 = 811+13 = 821+3 (# 32) 826 = 3+823 = 5+821 = 17+809 = 29+797 = 53+773 = 83+743 = 107+719 = 149+677 = 167+659 = 173+653 = 179+647 = 227+599 = 233+593 = 239+587 = 257+569 = 263+563 = 269+557 = 317+509 = 347+479 = 359+467 = 383+443 = 443+383 = 467+359 = 479+347 = 509+317 = 557+269 = 563+263 = 569+257 = 587+239 = 593+233 = 599+227 = 647+179 = 653+173 = 659+167 = 677+149 = 719+107 = 743+83 = 773+53 = 797+29 = 809+17 = 821+5 = 823+3 (# 42) 828 = 5+823 = 7+821 = 17+811 = 19+809 = 31+797 = 41+787 = 59+769 = 67+761 = 71+757 = 89+739 = 101+727 = 109+719 = 127+701 = 137+691 = 151+677 = 167+661 = 181+647 = 197+631 = 211+617 = 227+601 = 229+599 = 241+587 = 251+577 = 257+571 = 271+557 = 281+547 = 307+521 = 337+491 = 349+479 = 367+461 = 379+449 = 389+439 = 397+431 = 409+419 = 419+409 = 431+397 = 439+389 = 449+379 = 461+367 = 479+349 = 491+337 = 521+307 = 547+281 = 557+271 = 571+257 = 577+251 = 587+241 = 599+229 = 601+227 = 617+211 = 631+197 = 647+181 = 661+167 = 677+151 = 691+137 = 701+127 = 719+109 = 727+101 = 739+89 = 757+71 = 761+67 = 769+59 = 787+41 = 797+31 = 809+19 = 811+17 = 821+7 = 823+5 (# 68) 830 = 3+827 = 7+823 = 19+811 = 43+787 = 61+769 = 73+757 = 79+751 = 97+733 = 103+727 = 139+691 = 157+673 = 199+631 = 211+619 = 223+607 = 229+601 = 283+547 = 307+523 = 331+499 = 367+463 = 373+457 = 397+433 = 409+421 = 421+409 = 433+397 = 457+373 = 463+367 = 499+331 = 523+307 = 547+283 = 601+229 = 607+223 = 619+211 = 631+199 = 673+157 = 691+139 = 727+103 = 733+97 = 751+79 = 757+73 = 769+61 = 787+43 = 811+19 = 823+7 = 827+3 (# 44) 832 = 3+829 = 5+827 = 11+821 = 23+809 = 59+773 = 71+761 = 89+743 = 113+719 = 131+701 = 149+683 = 173+659 = 179+653 = 191+641 = 233+599 = 239+593 = 263+569 = 269+563 = 311+521 = 353+479 = 383+449 = 389+443 = 401+431 = 431+401 = 443+389 = 449+383 = 479+353 = 521+311 = 563+269 = 569+263 = 593+239 = 599+233 = 641+191 = 653+179 = 659+173 = 683+149 = 701+131 = 719+113 = 743+89 = 761+71 = 773+59 = 809+23 = 821+11 = 827+5 = 829+3 (# 44) 834 = 5+829 = 7+827 = 11+823 = 13+821 = 23+811 = 37+797 = 47+787 = 61+773 = 73+761 = 83+751 = 101+733 = 107+727 = 151+683 = 157+677 = 173+661 = 181+653 = 191+643 = 193+641 = 227+607 = 233+601 = 241+593 = 257+577 = 263+571 = 271+563 = 277+557 = 293+541 = 311+523 = 313+521 = 331+503 = 347+487 = 367+467 = 373+461 = 401+433 = 433+401 = 461+373 = 467+367 = 487+347 = 503+331 = 521+313 = 523+311 = 541+293 = 557+277 = 563+271 = 571+263 = 577+257 = 593+241 = 601+233 = 607+227 = 641+193 = 643+191 = 653+181 = 661+173 = 677+157 = 683+151 = 727+107 = 733+101 = 751+83 = 761+73 = 773+61 = 787+47 = 797+37 = 811+23 = 821+13 = 823+11 = 827+7 = 829+5 (# 66) 836 = 7+829 = 13+823 = 67+769 = 79+757 = 97+739 = 103+733 = 109+727 = 127+709 = 163+673 = 193+643 = 223+613 = 229+607 = 313+523 = 337+499 = 349+487 = 373+463 = 379+457 = 397+439 = 439+397 = 457+379 = 463+373 = 487+349 = 499+337 = 523+313 = 607+229 = 613+223 = 643+193 = 673+163 = 709+127 = 727+109 = 733+103 = 739+97 = 757+79 = 769+67 = 823+13 = 829+7 (# 36) 838 = 11+827 = 17+821 = 29+809 = 41+797 = 137+701 = 179+659 = 191+647 = 197+641 = 239+599 = 251+587 = 269+569 = 281+557 = 317+521 = 347+491 = 359+479 = 389+449 = 419+419 = 449+389 = 479+359 = 491+347 = 521+317 = 557+281 = 569+269 = 587+251 = 599+239 = 641+197 = 647+191 = 659+179 = 701+137 = 797+41 = 809+29 = 821+17 = 827+11 (# 33) 840 = 11+829 = 13+827 = 17+823 = 19+821 = 29+811 = 31+809 = 43+797 = 53+787 = 67+773 = 71+769 = 79+761 = 83+757 = 89+751 = 97+743 = 101+739 = 107+733 = 113+727 = 131+709 = 139+701 = 149+691 = 157+683 = 163+677 = 167+673 = 179+661 = 181+659 = 193+647 = 197+643 = 199+641 = 223+617 = 227+613 = 233+607 = 239+601 = 241+599 = 263+577 = 269+571 = 271+569 = 277+563 = 283+557 = 293+547 = 317+523 = 331+509 = 337+503 = 349+491 = 353+487 = 373+467 = 379+461 = 383+457 = 397+443 = 401+439 = 409+431 = 419+421 = 421+419 = 431+409 = 439+401 = 443+397 = 457+383 = 461+379 = 467+373 = 487+353 = 491+349 = 503+337 = 509+331 = 523+317 = 547+293 = 557+283 = 563+277 = 569+271 = 571+269 = 577+263 = 599+241 = 601+239 = 607+233 = 613+227 = 617+223 = 641+199 = 643+197 = 647+193 = 659+181 = 661+179 = 673+167 = 677+163 = 683+157 = 691+149 = 701+139 = 709+131 = 727+113 = 733+107 = 739+101 = 743+97 = 751+89 = 757+83 = 761+79 = 769+71 = 773+67 = 787+53 = 797+43 = 809+31 = 811+29 = 821+19 = 823+17 = 827+13 = 829+11 (# 102) 842 = 3+839 = 13+829 = 19+823 = 31+811 = 73+769 = 103+739 = 109+733 = 151+691 = 181+661 = 199+643 = 211+631 = 223+619 = 229+613 = 241+601 = 271+571 = 379+463 = 409+433 = 421+421 = 433+409 = 463+379 = 571+271 = 601+241 = 613+229 = 619+223 = 631+211 = 643+199 = 661+181 = 691+151 = 733+109 = 739+103 = 769+73 = 811+31 = 823+19 = 829+13 = 839+3 (# 35) 844 = 5+839 = 17+827 = 23+821 = 47+797 = 71+773 = 83+761 = 101+743 = 167+677 = 191+653 = 197+647 = 227+617 = 251+593 = 257+587 = 281+563 = 353+491 = 383+461 = 401+443 = 443+401 = 461+383 = 491+353 = 563+281 = 587+257 = 593+251 = 617+227 = 647+197 = 653+191 = 677+167 = 743+101 = 761+83 = 773+71 = 797+47 = 821+23 = 827+17 = 839+5 (# 34) 846 = 7+839 = 17+829 = 19+827 = 23+823 = 37+809 = 59+787 = 73+773 = 89+757 = 103+743 = 107+739 = 113+733 = 127+719 = 137+709 = 163+683 = 173+673 = 193+653 = 199+647 = 227+619 = 229+617 = 233+613 = 239+607 = 269+577 = 277+569 = 283+563 = 337+509 = 347+499 = 359+487 = 367+479 = 379+467 = 383+463 = 389+457 = 397+449 = 449+397 = 457+389 = 463+383 = 467+379 = 479+367 = 487+359 = 499+347 = 509+337 = 563+283 = 569+277 = 577+269 = 607+239 = 613+233 = 617+229 = 619+227 = 647+199 = 653+193 = 673+173 = 683+163 = 709+137 = 719+127 = 733+113 = 739+107 = 743+103 = 757+89 = 773+73 = 787+59 = 809+37 = 823+23 = 827+19 = 829+17 = 839+7 (# 64) 848 = 19+829 = 37+811 = 61+787 = 79+769 = 97+751 = 109+739 = 139+709 = 157+691 = 229+619 = 241+607 = 271+577 = 277+571 = 307+541 = 349+499 = 409+439 = 439+409 = 499+349 = 541+307 = 571+277 = 577+271 = 607+241 = 619+229 = 691+157 = 709+139 = 739+109 = 751+97 = 769+79 = 787+61 = 811+37 = 829+19 (# 30) 850 = 11+839 = 23+827 = 29+821 = 41+809 = 53+797 = 89+761 = 107+743 = 131+719 = 149+701 = 167+683 = 173+677 = 191+659 = 197+653 = 233+617 = 251+599 = 257+593 = 263+587 = 281+569 = 293+557 = 347+503 = 359+491 = 383+467 = 389+461 = 401+449 = 419+431 = 431+419 = 449+401 = 461+389 = 467+383 = 491+359 = 503+347 = 557+293 = 569+281 = 587+263 = 593+257 = 599+251 = 617+233 = 653+197 = 659+191 = 677+173 = 683+167 = 701+149 = 719+131 = 743+107 = 761+89 = 797+53 = 809+41 = 821+29 = 827+23 = 839+11 (# 50) 852 = 13+839 = 23+829 = 29+823 = 31+821 = 41+811 = 43+809 = 79+773 = 83+769 = 101+751 = 109+743 = 113+739 = 151+701 = 179+673 = 191+661 = 193+659 = 199+653 = 211+641 = 233+619 = 239+613 = 251+601 = 281+571 = 283+569 = 311+541 = 331+521 = 349+503 = 353+499 = 373+479 = 389+463 = 409+443 = 419+433 = 421+431 = 431+421 = 433+419 = 443+409 = 463+389 = 479+373 = 499+353 = 503+349 = 521+331 = 541+311 = 569+283 = 571+281 = 601+251 = 613+239 = 619+233 = 641+211 = 653+199 = 659+193 = 661+191 = 673+179 = 701+151 = 739+113 = 743+109 = 751+101 = 769+83 = 773+79 = 809+43 = 811+41 = 821+31 = 823+29 = 829+23 = 839+13 (# 62) 854 = 31+823 = 43+811 = 67+787 = 97+757 = 103+751 = 127+727 = 163+691 = 181+673 = 193+661 = 211+643 = 223+631 = 241+613 = 277+577 = 283+571 = 307+547 = 313+541 = 331+523 = 367+487 = 397+457 = 421+433 = 433+421 = 457+397 = 487+367 = 523+331 = 541+313 = 547+307 = 571+283 = 577+277 = 613+241 = 631+223 = 643+211 = 661+193 = 673+181 = 691+163 = 727+127 = 751+103 = 757+97 = 787+67 = 811+43 = 823+31 (# 40) 856 = 3+853 = 17+839 = 29+827 = 47+809 = 59+797 = 83+773 = 113+743 = 137+719 = 173+683 = 179+677 = 197+659 = 239+617 = 257+599 = 263+593 = 269+587 = 293+563 = 347+509 = 353+503 = 389+467 = 467+389 = 503+353 = 509+347 = 563+293 = 587+269 = 593+263 = 599+257 = 617+239 = 659+197 = 677+179 = 683+173 = 719+137 = 743+113 = 773+83 = 797+59 = 809+47 = 827+29 = 839+17 = 853+3 (# 38) 858 = 5+853 = 19+839 = 29+829 = 31+827 = 37+821 = 47+811 = 61+797 = 71+787 = 89+769 = 97+761 = 101+757 = 107+751 = 131+727 = 139+719 = 149+709 = 157+701 = 167+691 = 181+677 = 197+661 = 199+659 = 211+647 = 227+631 = 239+619 = 241+617 = 251+607 = 257+601 = 271+587 = 281+577 = 311+547 = 317+541 = 337+521 = 349+509 = 359+499 = 367+491 = 379+479 = 397+461 = 401+457 = 409+449 = 419+439 = 439+419 = 449+409 = 457+401 = 461+397 = 479+379 = 491+367 = 499+359 = 509+349 = 521+337 = 541+317 = 547+311 = 577+281 = 587+271 = 601+257 = 607+251 = 617+241 = 619+239 = 631+227 = 647+211 = 659+199 = 661+197 = 677+181 = 691+167 = 701+157 = 709+149 = 719+139 = 727+131 = 751+107 = 757+101 = 761+97 = 769+89 = 787+71 = 797+61 = 811+47 = 821+37 = 827+31 = 829+29 = 839+19 = 853+5 (# 78) 860 = 3+857 = 7+853 = 31+829 = 37+823 = 73+787 = 103+757 = 109+751 = 127+733 = 151+709 = 199+661 = 229+631 = 241+619 = 283+577 = 313+547 = 337+523 = 373+487 = 397+463 = 421+439 = 439+421 = 463+397 = 487+373 = 523+337 = 547+313 = 577+283 = 619+241 = 631+229 = 661+199 = 709+151 = 733+127 = 751+109 = 757+103 = 787+73 = 823+37 = 829+31 = 853+7 = 857+3 (# 36) 862 = 3+859 = 5+857 = 23+839 = 41+821 = 53+809 = 89+773 = 101+761 = 179+683 = 263+599 = 269+593 = 293+569 = 353+509 = 359+503 = 383+479 = 401+461 = 419+443 = 431+431 = 443+419 = 461+401 = 479+383 = 503+359 = 509+353 = 569+293 = 593+269 = 599+263 = 683+179 = 761+101 = 773+89 = 809+53 = 821+41 = 839+23 = 857+5 = 859+3 (# 33) 864 = 5+859 = 7+857 = 11+853 = 37+827 = 41+823 = 43+821 = 53+811 = 67+797 = 103+761 = 107+757 = 113+751 = 131+733 = 137+727 = 163+701 = 173+691 = 181+683 = 191+673 = 211+653 = 223+641 = 233+631 = 251+613 = 257+607 = 263+601 = 271+593 = 277+587 = 293+571 = 307+557 = 317+547 = 373+491 = 397+467 = 401+463 = 421+443 = 431+433 = 433+431 = 443+421 = 463+401 = 467+397 = 491+373 = 547+317 = 557+307 = 571+293 = 587+277 = 593+271 = 601+263 = 607+257 = 613+251 = 631+233 = 641+223 = 653+211 = 673+191 = 683+181 = 691+173 = 701+163 = 727+137 = 733+131 = 751+113 = 757+107 = 761+103 = 797+67 = 811+53 = 821+43 = 823+41 = 827+37 = 853+11 = 857+7 = 859+5 (# 66) 866 = 3+863 = 7+859 = 13+853 = 37+829 = 43+823 = 79+787 = 97+769 = 109+757 = 127+739 = 139+727 = 157+709 = 193+673 = 223+643 = 367+499 = 379+487 = 409+457 = 433+433 = 457+409 = 487+379 = 499+367 = 643+223 = 673+193 = 709+157 = 727+139 = 739+127 = 757+109 = 769+97 = 787+79 = 823+43 = 829+37 = 853+13 = 859+7 = 863+3 (# 33) 868 = 5+863 = 11+857 = 29+839 = 41+827 = 47+821 = 59+809 = 71+797 = 107+761 = 149+719 = 167+701 = 191+677 = 227+641 = 251+617 = 269+599 = 281+587 = 311+557 = 347+521 = 359+509 = 389+479 = 401+467 = 419+449 = 449+419 = 467+401 = 479+389 = 509+359 = 521+347 = 557+311 = 587+281 = 599+269 = 617+251 = 641+227 = 677+191 = 701+167 = 719+149 = 761+107 = 797+71 = 809+59 = 821+47 = 827+41 = 839+29 = 857+11 = 863+5 (# 42) 870 = 7+863 = 11+859 = 13+857 = 17+853 = 31+839 = 41+829 = 43+827 = 47+823 = 59+811 = 61+809 = 73+797 = 83+787 = 97+773 = 101+769 = 109+761 = 113+757 = 127+743 = 131+739 = 137+733 = 151+719 = 179+691 = 193+677 = 197+673 = 211+659 = 223+647 = 227+643 = 229+641 = 239+631 = 251+619 = 257+613 = 263+607 = 269+601 = 271+599 = 277+593 = 283+587 = 293+577 = 307+563 = 313+557 = 347+523 = 349+521 = 367+503 = 379+491 = 383+487 = 409+461 = 421+449 = 431+439 = 439+431 = 449+421 = 461+409 = 487+383 = 491+379 = 503+367 = 521+349 = 523+347 = 557+313 = 563+307 = 577+293 = 587+283 = 593+277 = 599+271 = 601+269 = 607+263 = 613+257 = 619+251 = 631+239 = 641+229 = 643+227 = 647+223 = 659+211 = 673+197 = 677+193 = 691+179 = 719+151 = 733+137 = 739+131 = 743+127 = 757+113 = 761+109 = 769+101 = 773+97 = 787+83 = 797+73 = 809+61 = 811+59 = 823+47 = 827+43 = 829+41 = 839+31 = 853+17 = 857+13 = 859+11 = 863+7 (# 92) 872 = 13+859 = 19+853 = 43+829 = 61+811 = 103+769 = 139+733 = 163+709 = 181+691 = 199+673 = 211+661 = 229+643 = 241+631 = 271+601 = 331+541 = 349+523 = 373+499 = 409+463 = 433+439 = 439+433 = 463+409 = 499+373 = 523+349 = 541+331 = 601+271 = 631+241 = 643+229 = 661+211 = 673+199 = 691+181 = 709+163 = 733+139 = 769+103 = 811+61 = 829+43 = 853+19 = 859+13 (# 36) 874 = 11+863 = 17+857 = 47+827 = 53+821 = 101+773 = 113+761 = 131+743 = 173+701 = 191+683 = 197+677 = 227+647 = 233+641 = 257+617 = 281+593 = 311+563 = 317+557 = 353+521 = 383+491 = 431+443 = 443+431 = 491+383 = 521+353 = 557+317 = 563+311 = 593+281 = 617+257 = 641+233 = 647+227 = 677+197 = 683+191 = 701+173 = 743+131 = 761+113 = 773+101 = 821+53 = 827+47 = 857+17 = 863+11 (# 38) 876 = 13+863 = 17+859 = 19+857 = 23+853 = 37+839 = 47+829 = 53+823 = 67+809 = 79+797 = 89+787 = 103+773 = 107+769 = 137+739 = 149+727 = 157+719 = 167+709 = 193+683 = 199+677 = 223+653 = 229+647 = 233+643 = 257+619 = 263+613 = 269+607 = 277+599 = 283+593 = 307+569 = 313+563 = 353+523 = 367+509 = 373+503 = 389+487 = 397+479 = 409+467 = 419+457 = 433+443 = 443+433 = 457+419 = 467+409 = 479+397 = 487+389 = 503+373 = 509+367 = 523+353 = 563+313 = 569+307 = 593+283 = 599+277 = 607+269 = 613+263 = 619+257 = 643+233 = 647+229 = 653+223 = 677+199 = 683+193 = 709+167 = 719+157 = 727+149 = 739+137 = 769+107 = 773+103 = 787+89 = 797+79 = 809+67 = 823+53 = 829+47 = 839+37 = 853+23 = 857+19 = 859+17 = 863+13 (# 72) 878 = 19+859 = 67+811 = 109+769 = 127+751 = 139+739 = 151+727 = 271+607 = 277+601 = 307+571 = 331+547 = 337+541 = 379+499 = 421+457 = 439+439 = 457+421 = 499+379 = 541+337 = 547+331 = 571+307 = 601+277 = 607+271 = 727+151 = 739+139 = 751+127 = 769+109 = 811+67 = 859+19 (# 27) 880 = 3+877 = 17+863 = 23+857 = 41+839 = 53+827 = 59+821 = 71+809 = 83+797 = 107+773 = 137+743 = 179+701 = 197+683 = 227+653 = 233+647 = 239+641 = 263+617 = 281+599 = 293+587 = 311+569 = 317+563 = 359+521 = 389+491 = 401+479 = 419+461 = 431+449 = 449+431 = 461+419 = 479+401 = 491+389 = 521+359 = 563+317 = 569+311 = 587+293 = 599+281 = 617+263 = 641+239 = 647+233 = 653+227 = 683+197 = 701+179 = 743+137 = 773+107 = 797+83 = 809+71 = 821+59 = 827+53 = 839+41 = 857+23 = 863+17 = 877+3 (# 50) 882 = 5+877 = 19+863 = 23+859 = 29+853 = 43+839 = 53+829 = 59+823 = 61+821 = 71+811 = 73+809 = 109+773 = 113+769 = 131+751 = 139+743 = 149+733 = 163+719 = 173+709 = 181+701 = 191+691 = 199+683 = 223+659 = 229+653 = 239+643 = 241+641 = 251+631 = 263+619 = 269+613 = 281+601 = 283+599 = 311+571 = 313+569 = 359+523 = 373+509 = 379+503 = 383+499 = 419+463 = 421+461 = 433+449 = 439+443 = 443+439 = 449+433 = 461+421 = 463+419 = 499+383 = 503+379 = 509+373 = 523+359 = 569+313 = 571+311 = 599+283 = 601+281 = 613+269 = 619+263 = 631+251 = 641+241 = 643+239 = 653+229 = 659+223 = 683+199 = 691+191 = 701+181 = 709+173 = 719+163 = 733+149 = 743+139 = 751+131 = 769+113 = 773+109 = 809+73 = 811+71 = 821+61 = 823+59 = 829+53 = 839+43 = 853+29 = 859+23 = 863+19 = 877+5 (# 78) 884 = 3+881 = 7+877 = 31+853 = 61+823 = 73+811 = 97+787 = 127+757 = 151+733 = 157+727 = 193+691 = 211+673 = 223+661 = 241+643 = 271+613 = 277+607 = 283+601 = 307+577 = 313+571 = 337+547 = 397+487 = 421+463 = 463+421 = 487+397 = 547+337 = 571+313 = 577+307 = 601+283 = 607+277 = 613+271 = 643+241 = 661+223 = 673+211 = 691+193 = 727+157 = 733+151 = 757+127 = 787+97 = 811+73 = 823+61 = 853+31 = 877+7 = 881+3 (# 42) 886 = 3+883 = 5+881 = 23+863 = 29+857 = 47+839 = 59+827 = 89+797 = 113+773 = 167+719 = 227+659 = 233+653 = 239+647 = 269+617 = 293+593 = 317+569 = 383+503 = 419+467 = 443+443 = 467+419 = 503+383 = 569+317 = 593+293 = 617+269 = 647+239 = 653+233 = 659+227 = 719+167 = 773+113 = 797+89 = 827+59 = 839+47 = 857+29 = 863+23 = 881+5 = 883+3 (# 35) 888 = 5+883 = 7+881 = 11+877 = 29+859 = 31+857 = 59+829 = 61+827 = 67+821 = 79+809 = 101+787 = 127+761 = 131+757 = 137+751 = 149+739 = 179+709 = 197+691 = 211+677 = 227+661 = 229+659 = 241+647 = 257+631 = 269+619 = 271+617 = 281+607 = 311+577 = 317+571 = 331+557 = 347+541 = 367+521 = 379+509 = 389+499 = 397+491 = 401+487 = 409+479 = 421+467 = 431+457 = 439+449 = 449+439 = 457+431 = 467+421 = 479+409 = 487+401 = 491+397 = 499+389 = 509+379 = 521+367 = 541+347 = 557+331 = 571+317 = 577+311 = 607+281 = 617+271 = 619+269 = 631+257 = 647+241 = 659+229 = 661+227 = 677+211 = 691+197 = 709+179 = 739+149 = 751+137 = 757+131 = 761+127 = 787+101 = 809+79 = 821+67 = 827+61 = 829+59 = 857+31 = 859+29 = 877+11 = 881+7 = 883+5 (# 74) 890 = 3+887 = 7+883 = 13+877 = 31+859 = 37+853 = 61+829 = 67+823 = 79+811 = 103+787 = 139+751 = 151+739 = 157+733 = 163+727 = 181+709 = 199+691 = 229+661 = 271+619 = 277+613 = 283+607 = 313+577 = 349+541 = 367+523 = 433+457 = 457+433 = 523+367 = 541+349 = 577+313 = 607+283 = 613+277 = 619+271 = 661+229 = 691+199 = 709+181 = 727+163 = 733+157 = 739+151 = 751+139 = 787+103 = 811+79 = 823+67 = 829+61 = 853+37 = 859+31 = 877+13 = 883+7 = 887+3 (# 46) 892 = 5+887 = 11+881 = 29+863 = 53+839 = 71+821 = 83+809 = 131+761 = 149+743 = 173+719 = 191+701 = 233+659 = 239+653 = 251+641 = 293+599 = 383+509 = 389+503 = 401+491 = 431+461 = 443+449 = 449+443 = 461+431 = 491+401 = 503+389 = 509+383 = 599+293 = 641+251 = 653+239 = 659+233 = 701+191 = 719+173 = 743+149 = 761+131 = 809+83 = 821+71 = 839+53 = 863+29 = 881+11 = 887+5 (# 38) 894 = 7+887 = 11+883 = 13+881 = 17+877 = 31+863 = 37+857 = 41+853 = 67+827 = 71+823 = 73+821 = 83+811 = 97+797 = 107+787 = 137+757 = 151+743 = 167+727 = 193+701 = 211+683 = 233+661 = 241+653 = 251+643 = 263+631 = 277+617 = 281+613 = 293+601 = 307+587 = 317+577 = 331+563 = 337+557 = 347+547 = 353+541 = 373+521 = 431+463 = 433+461 = 461+433 = 463+431 = 521+373 = 541+353 = 547+347 = 557+337 = 563+331 = 577+317 = 587+307 = 601+293 = 613+281 = 617+277 = 631+263 = 643+251 = 653+241 = 661+233 = 683+211 = 701+193 = 727+167 = 743+151 = 757+137 = 787+107 = 797+97 = 811+83 = 821+73 = 823+71 = 827+67 = 853+41 = 857+37 = 863+31 = 877+17 = 881+13 = 883+11 = 887+7 (# 68) 896 = 13+883 = 19+877 = 37+859 = 43+853 = 67+829 = 73+823 = 109+787 = 127+769 = 139+757 = 157+739 = 163+733 = 223+673 = 277+619 = 283+613 = 349+547 = 373+523 = 397+499 = 409+487 = 433+463 = 439+457 = 457+439 = 463+433 = 487+409 = 499+397 = 523+373 = 547+349 = 613+283 = 619+277 = 673+223 = 733+163 = 739+157 = 757+139 = 769+127 = 787+109 = 823+73 = 829+67 = 853+43 = 859+37 = 877+19 = 883+13 (# 40) 898 = 11+887 = 17+881 = 41+857 = 59+839 = 71+827 = 89+809 = 101+797 = 137+761 = 179+719 = 197+701 = 239+659 = 251+647 = 257+641 = 281+617 = 311+587 = 389+509 = 419+479 = 431+467 = 449+449 = 467+431 = 479+419 = 509+389 = 587+311 = 617+281 = 641+257 = 647+251 = 659+239 = 701+197 = 719+179 = 761+137 = 797+101 = 809+89 = 827+71 = 839+59 = 857+41 = 881+17 = 887+11 (# 37) 900 = 13+887 = 17+883 = 19+881 = 23+877 = 37+863 = 41+859 = 43+857 = 47+853 = 61+839 = 71+829 = 73+827 = 79+821 = 89+811 = 103+797 = 113+787 = 127+773 = 131+769 = 139+761 = 149+751 = 157+743 = 167+733 = 173+727 = 181+719 = 191+709 = 199+701 = 223+677 = 227+673 = 239+661 = 241+659 = 257+643 = 269+631 = 281+619 = 283+617 = 293+607 = 307+593 = 313+587 = 331+569 = 337+563 = 353+547 = 359+541 = 379+521 = 397+503 = 401+499 = 409+491 = 421+479 = 433+467 = 439+461 = 443+457 = 457+443 = 461+439 = 467+433 = 479+421 = 491+409 = 499+401 = 503+397 = 521+379 = 541+359 = 547+353 = 563+337 = 569+331 = 587+313 = 593+307 = 607+293 = 617+283 = 619+281 = 631+269 = 643+257 = 659+241 = 661+239 = 673+227 = 677+223 = 701+199 = 709+191 = 719+181 = 727+173 = 733+167 = 743+157 = 751+149 = 761+139 = 769+131 = 773+127 = 787+113 = 797+103 = 811+89 = 821+79 = 827+73 = 829+71 = 839+61 = 853+47 = 857+43 = 859+41 = 863+37 = 877+23 = 881+19 = 883+17 = 887+13 (# 96) 902 = 19+883 = 43+859 = 73+829 = 79+823 = 151+751 = 163+739 = 193+709 = 211+691 = 229+673 = 241+661 = 271+631 = 283+619 = 331+571 = 379+523 = 439+463 = 463+439 = 523+379 = 571+331 = 619+283 = 631+271 = 661+241 = 673+229 = 691+211 = 709+193 = 739+163 = 751+151 = 823+79 = 829+73 = 859+43 = 883+19 (# 30) 904 = 17+887 = 23+881 = 41+863 = 47+857 = 83+821 = 107+797 = 131+773 = 227+677 = 251+653 = 257+647 = 263+641 = 311+593 = 317+587 = 347+557 = 383+521 = 401+503 = 443+461 = 461+443 = 503+401 = 521+383 = 557+347 = 587+317 = 593+311 = 641+263 = 647+257 = 653+251 = 677+227 = 773+131 = 797+107 = 821+83 = 857+47 = 863+41 = 881+23 = 887+17 (# 34) 906 = 19+887 = 23+883 = 29+877 = 43+863 = 47+859 = 53+853 = 67+839 = 79+827 = 83+823 = 97+809 = 109+797 = 137+769 = 149+757 = 163+743 = 167+739 = 173+733 = 179+727 = 197+709 = 223+683 = 229+677 = 233+673 = 263+643 = 293+613 = 307+599 = 313+593 = 337+569 = 349+557 = 359+547 = 383+523 = 397+509 = 419+487 = 439+467 = 443+463 = 449+457 = 457+449 = 463+443 = 467+439 = 487+419 = 509+397 = 523+383 = 547+359 = 557+349 = 569+337 = 593+313 = 599+307 = 613+293 = 643+263 = 673+233 = 677+229 = 683+223 = 709+197 = 727+179 = 733+173 = 739+167 = 743+163 = 757+149 = 769+137 = 797+109 = 809+97 = 823+83 = 827+79 = 839+67 = 853+53 = 859+47 = 863+43 = 877+29 = 883+23 = 887+19 (# 68) 908 = 31+877 = 79+829 = 97+811 = 139+769 = 151+757 = 157+751 = 181+727 = 199+709 = 277+631 = 307+601 = 331+577 = 337+571 = 367+541 = 409+499 = 421+487 = 487+421 = 499+409 = 541+367 = 571+337 = 577+331 = 601+307 = 631+277 = 709+199 = 727+181 = 751+157 = 757+151 = 769+139 = 811+97 = 829+79 = 877+31 (# 30) 910 = 3+907 = 23+887 = 29+881 = 47+863 = 53+857 = 71+839 = 83+827 = 89+821 = 101+809 = 113+797 = 137+773 = 149+761 = 167+743 = 191+719 = 227+683 = 233+677 = 251+659 = 257+653 = 263+647 = 269+641 = 293+617 = 311+599 = 317+593 = 347+563 = 353+557 = 389+521 = 401+509 = 419+491 = 431+479 = 443+467 = 449+461 = 461+449 = 467+443 = 479+431 = 491+419 = 509+401 = 521+389 = 557+353 = 563+347 = 593+317 = 599+311 = 617+293 = 641+269 = 647+263 = 653+257 = 659+251 = 677+233 = 683+227 = 719+191 = 743+167 = 761+149 = 773+137 = 797+113 = 809+101 = 821+89 = 827+83 = 839+71 = 857+53 = 863+47 = 881+29 = 887+23 = 907+3 (# 62) 912 = 5+907 = 29+883 = 31+881 = 53+859 = 59+853 = 73+839 = 83+829 = 89+823 = 101+811 = 103+809 = 139+773 = 151+761 = 173+739 = 179+733 = 193+719 = 211+701 = 229+683 = 239+673 = 251+661 = 269+643 = 271+641 = 281+631 = 293+619 = 311+601 = 313+599 = 349+563 = 389+523 = 409+503 = 421+491 = 433+479 = 449+463 = 463+449 = 479+433 = 491+421 = 503+409 = 523+389 = 563+349 = 599+313 = 601+311 = 619+293 = 631+281 = 641+271 = 643+269 = 661+251 = 673+239 = 683+229 = 701+211 = 719+193 = 733+179 = 739+173 = 761+151 = 773+139 = 809+103 = 811+101 = 823+89 = 829+83 = 839+73 = 853+59 = 859+53 = 881+31 = 883+29 = 907+5 (# 62) 914 = 3+911 = 7+907 = 31+883 = 37+877 = 61+853 = 103+811 = 127+787 = 157+757 = 163+751 = 181+733 = 223+691 = 241+673 = 271+643 = 283+631 = 307+607 = 313+601 = 337+577 = 367+547 = 373+541 = 457+457 = 541+373 = 547+367 = 577+337 = 601+313 = 607+307 = 631+283 = 643+271 = 673+241 = 691+223 = 733+181 = 751+163 = 757+157 = 787+127 = 811+103 = 853+61 = 877+37 = 883+31 = 907+7 = 911+3 (# 39) 916 = 5+911 = 29+887 = 53+863 = 59+857 = 89+827 = 107+809 = 173+743 = 197+719 = 233+683 = 239+677 = 257+659 = 263+653 = 269+647 = 317+599 = 347+569 = 353+563 = 359+557 = 449+467 = 467+449 = 557+359 = 563+353 = 569+347 = 599+317 = 647+269 = 653+263 = 659+257 = 677+239 = 683+233 = 719+197 = 743+173 = 809+107 = 827+89 = 857+59 = 863+53 = 887+29 = 911+5 (# 36) 918 = 7+911 = 11+907 = 31+887 = 37+881 = 41+877 = 59+859 = 61+857 = 79+839 = 89+829 = 97+821 = 107+811 = 109+809 = 131+787 = 149+769 = 157+761 = 167+751 = 179+739 = 191+727 = 199+719 = 227+691 = 241+677 = 257+661 = 271+647 = 277+641 = 311+607 = 317+601 = 331+587 = 347+571 = 349+569 = 397+521 = 409+509 = 419+499 = 431+487 = 439+479 = 457+461 = 461+457 = 479+439 = 487+431 = 499+419 = 509+409 = 521+397 = 569+349 = 571+347 = 587+331 = 601+317 = 607+311 = 641+277 = 647+271 = 661+257 = 677+241 = 691+227 = 719+199 = 727+191 = 739+179 = 751+167 = 761+157 = 769+149 = 787+131 = 809+109 = 811+107 = 821+97 = 829+89 = 839+79 = 857+61 = 859+59 = 877+41 = 881+37 = 887+31 = 907+11 = 911+7 (# 70) 920 = 13+907 = 37+883 = 43+877 = 61+859 = 67+853 = 97+823 = 109+811 = 151+769 = 163+757 = 181+739 = 193+727 = 211+709 = 229+691 = 277+643 = 307+613 = 313+607 = 349+571 = 373+547 = 379+541 = 397+523 = 421+499 = 433+487 = 457+463 = 463+457 = 487+433 = 499+421 = 523+397 = 541+379 = 547+373 = 571+349 = 607+313 = 613+307 = 643+277 = 691+229 = 709+211 = 727+193 = 739+181 = 757+163 = 769+151 = 811+109 = 823+97 = 853+67 = 859+61 = 877+43 = 883+37 = 907+13 (# 46) 922 = 3+919 = 11+911 = 41+881 = 59+863 = 83+839 = 101+821 = 113+809 = 149+773 = 179+743 = 239+683 = 263+659 = 269+653 = 281+641 = 353+569 = 359+563 = 401+521 = 419+503 = 431+491 = 443+479 = 461+461 = 479+443 = 491+431 = 503+419 = 521+401 = 563+359 = 569+353 = 641+281 = 653+269 = 659+263 = 683+239 = 743+179 = 773+149 = 809+113 = 821+101 = 839+83 = 863+59 = 881+41 = 911+11 = 919+3 (# 39) 924 = 5+919 = 13+911 = 17+907 = 37+887 = 41+883 = 43+881 = 47+877 = 61+863 = 67+857 = 71+853 = 97+827 = 101+823 = 103+821 = 113+811 = 127+797 = 137+787 = 151+773 = 163+761 = 167+757 = 173+751 = 181+743 = 191+733 = 197+727 = 223+701 = 233+691 = 241+683 = 251+673 = 263+661 = 271+653 = 277+647 = 281+643 = 283+641 = 293+631 = 307+617 = 311+613 = 317+607 = 331+593 = 337+587 = 347+577 = 353+571 = 367+557 = 383+541 = 401+523 = 421+503 = 433+491 = 457+467 = 461+463 = 463+461 = 467+457 = 491+433 = 503+421 = 523+401 = 541+383 = 557+367 = 571+353 = 577+347 = 587+337 = 593+331 = 607+317 = 613+311 = 617+307 = 631+293 = 641+283 = 643+281 = 647+277 = 653+271 = 661+263 = 673+251 = 683+241 = 691+233 = 701+223 = 727+197 = 733+191 = 743+181 = 751+173 = 757+167 = 761+163 = 773+151 = 787+137 = 797+127 = 811+113 = 821+103 = 823+101 = 827+97 = 853+71 = 857+67 = 863+61 = 877+47 = 881+43 = 883+41 = 887+37 = 907+17 = 911+13 = 919+5 (# 94) 926 = 7+919 = 19+907 = 43+883 = 67+859 = 73+853 = 97+829 = 103+823 = 139+787 = 157+769 = 193+733 = 199+727 = 283+643 = 307+619 = 313+613 = 349+577 = 379+547 = 439+487 = 463+463 = 487+439 = 547+379 = 577+349 = 613+313 = 619+307 = 643+283 = 727+199 = 733+193 = 769+157 = 787+139 = 823+103 = 829+97 = 853+73 = 859+67 = 883+43 = 907+19 = 919+7 (# 35) 928 = 17+911 = 41+887 = 47+881 = 71+857 = 89+839 = 101+827 = 107+821 = 131+797 = 167+761 = 227+701 = 251+677 = 269+659 = 281+647 = 311+617 = 359+569 = 419+509 = 449+479 = 461+467 = 467+461 = 479+449 = 509+419 = 569+359 = 617+311 = 647+281 = 659+269 = 677+251 = 701+227 = 761+167 = 797+131 = 821+107 = 827+101 = 839+89 = 857+71 = 881+47 = 887+41 = 911+17 (# 36) 930 = 11+919 = 19+911 = 23+907 = 43+887 = 47+883 = 53+877 = 67+863 = 71+859 = 73+857 = 101+829 = 103+827 = 107+823 = 109+821 = 157+773 = 173+757 = 179+751 = 191+739 = 197+733 = 211+719 = 229+701 = 239+691 = 257+673 = 269+661 = 271+659 = 277+653 = 283+647 = 311+619 = 313+617 = 317+613 = 331+599 = 337+593 = 353+577 = 359+571 = 367+563 = 373+557 = 383+547 = 389+541 = 409+521 = 421+509 = 431+499 = 439+491 = 443+487 = 463+467 = 467+463 = 487+443 = 491+439 = 499+431 = 509+421 = 521+409 = 541+389 = 547+383 = 557+373 = 563+367 = 571+359 = 577+353 = 593+337 = 599+331 = 613+317 = 617+313 = 619+311 = 647+283 = 653+277 = 659+271 = 661+269 = 673+257 = 691+239 = 701+229 = 719+211 = 733+197 = 739+191 = 751+179 = 757+173 = 773+157 = 821+109 = 823+107 = 827+103 = 829+101 = 857+73 = 859+71 = 863+67 = 877+53 = 883+47 = 887+43 = 907+23 = 911+19 = 919+11 (# 86) 932 = 3+929 = 13+919 = 73+859 = 79+853 = 103+829 = 109+823 = 163+769 = 181+751 = 193+739 = 199+733 = 223+709 = 241+691 = 271+661 = 313+619 = 331+601 = 409+523 = 433+499 = 499+433 = 523+409 = 601+331 = 619+313 = 661+271 = 691+241 = 709+223 = 733+199 = 739+193 = 751+181 = 769+163 = 823+109 = 829+103 = 853+79 = 859+73 = 919+13 = 929+3 (# 34) 934 = 5+929 = 23+911 = 47+887 = 53+881 = 71+863 = 107+827 = 113+821 = 137+797 = 173+761 = 191+743 = 233+701 = 251+683 = 257+677 = 281+653 = 293+641 = 317+617 = 347+587 = 431+503 = 443+491 = 467+467 = 491+443 = 503+431 = 587+347 = 617+317 = 641+293 = 653+281 = 677+257 = 683+251 = 701+233 = 743+191 = 761+173 = 797+137 = 821+113 = 827+107 = 863+71 = 881+53 = 887+47 = 911+23 = 929+5 (# 39) 936 = 7+929 = 17+919 = 29+907 = 53+883 = 59+877 = 73+863 = 79+857 = 83+853 = 97+839 = 107+829 = 109+827 = 113+823 = 127+809 = 139+797 = 149+787 = 163+773 = 167+769 = 179+757 = 193+743 = 197+739 = 227+709 = 263+673 = 277+659 = 283+653 = 293+643 = 317+619 = 337+599 = 349+587 = 359+577 = 367+569 = 373+563 = 379+557 = 389+547 = 433+503 = 449+487 = 457+479 = 479+457 = 487+449 = 503+433 = 547+389 = 557+379 = 563+373 = 569+367 = 577+359 = 587+349 = 599+337 = 619+317 = 643+293 = 653+283 = 659+277 = 673+263 = 709+227 = 739+197 = 743+193 = 757+179 = 769+167 = 773+163 = 787+149 = 797+139 = 809+127 = 823+113 = 827+109 = 829+107 = 839+97 = 853+83 = 857+79 = 863+73 = 877+59 = 883+53 = 907+29 = 919+17 = 929+7 (# 72) 938 = 19+919 = 31+907 = 61+877 = 79+859 = 109+829 = 127+811 = 151+787 = 181+757 = 199+739 = 211+727 = 229+709 = 277+661 = 307+631 = 331+607 = 337+601 = 367+571 = 397+541 = 439+499 = 499+439 = 541+397 = 571+367 = 601+337 = 607+331 = 631+307 = 661+277 = 709+229 = 727+211 = 739+199 = 757+181 = 787+151 = 811+127 = 829+109 = 859+79 = 877+61 = 907+31 = 919+19 (# 36) 940 = 3+937 = 11+929 = 29+911 = 53+887 = 59+881 = 83+857 = 101+839 = 113+827 = 131+809 = 167+773 = 179+761 = 197+743 = 239+701 = 257+683 = 263+677 = 281+659 = 293+647 = 347+593 = 353+587 = 383+557 = 419+521 = 431+509 = 449+491 = 461+479 = 479+461 = 491+449 = 509+431 = 521+419 = 557+383 = 587+353 = 593+347 = 647+293 = 659+281 = 677+263 = 683+257 = 701+239 = 743+197 = 761+179 = 773+167 = 809+131 = 827+113 = 839+101 = 857+83 = 881+59 = 887+53 = 911+29 = 929+11 = 937+3 (# 48) 942 = 5+937 = 13+929 = 23+919 = 31+911 = 59+883 = 61+881 = 79+863 = 83+859 = 89+853 = 103+839 = 113+829 = 131+811 = 173+769 = 181+761 = 191+751 = 199+743 = 223+719 = 233+709 = 241+701 = 251+691 = 269+673 = 281+661 = 283+659 = 311+631 = 349+593 = 373+569 = 379+563 = 401+541 = 419+523 = 421+521 = 433+509 = 439+503 = 443+499 = 463+479 = 479+463 = 499+443 = 503+439 = 509+433 = 521+421 = 523+419 = 541+401 = 563+379 = 569+373 = 593+349 = 631+311 = 659+283 = 661+281 = 673+269 = 691+251 = 701+241 = 709+233 = 719+223 = 743+199 = 751+191 = 761+181 = 769+173 = 811+131 = 829+113 = 839+103 = 853+89 = 859+83 = 863+79 = 881+61 = 883+59 = 911+31 = 919+23 = 929+13 = 937+5 (# 68) 944 = 3+941 = 7+937 = 37+907 = 61+883 = 67+877 = 157+787 = 193+751 = 211+733 = 271+673 = 283+661 = 313+631 = 331+613 = 337+607 = 367+577 = 373+571 = 397+547 = 421+523 = 457+487 = 487+457 = 523+421 = 547+397 = 571+373 = 577+367 = 607+337 = 613+331 = 631+313 = 661+283 = 673+271 = 733+211 = 751+193 = 787+157 = 877+67 = 883+61 = 907+37 = 937+7 = 941+3 (# 36) 946 = 5+941 = 17+929 = 59+887 = 83+863 = 89+857 = 107+839 = 137+809 = 149+797 = 173+773 = 227+719 = 263+683 = 269+677 = 293+653 = 347+599 = 353+593 = 359+587 = 383+563 = 389+557 = 443+503 = 467+479 = 479+467 = 503+443 = 557+389 = 563+383 = 587+359 = 593+353 = 599+347 = 653+293 = 677+269 = 683+263 = 719+227 = 773+173 = 797+149 = 809+137 = 839+107 = 857+89 = 863+83 = 887+59 = 929+17 = 941+5 (# 40) 948 = 7+941 = 11+937 = 19+929 = 29+919 = 37+911 = 41+907 = 61+887 = 67+881 = 71+877 = 89+859 = 109+839 = 127+821 = 137+811 = 139+809 = 151+797 = 179+769 = 191+757 = 197+751 = 229+719 = 239+709 = 257+691 = 271+677 = 307+641 = 317+631 = 331+617 = 347+601 = 349+599 = 379+569 = 401+547 = 439+509 = 449+499 = 457+491 = 461+487 = 487+461 = 491+457 = 499+449 = 509+439 = 547+401 = 569+379 = 599+349 = 601+347 = 617+331 = 631+317 = 641+307 = 677+271 = 691+257 = 709+239 = 719+229 = 751+197 = 757+191 = 769+179 = 797+151 = 809+139 = 811+137 = 821+127 = 839+109 = 859+89 = 877+71 = 881+67 = 887+61 = 907+41 = 911+37 = 919+29 = 929+19 = 937+11 = 941+7 (# 66) 950 = 3+947 = 13+937 = 31+919 = 43+907 = 67+883 = 73+877 = 97+853 = 127+823 = 139+811 = 163+787 = 181+769 = 193+757 = 199+751 = 211+739 = 223+727 = 241+709 = 277+673 = 307+643 = 331+619 = 337+613 = 349+601 = 373+577 = 379+571 = 409+541 = 463+487 = 487+463 = 541+409 = 571+379 = 577+373 = 601+349 = 613+337 = 619+331 = 643+307 = 673+277 = 709+241 = 727+223 = 739+211 = 751+199 = 757+193 = 769+181 = 787+163 = 811+139 = 823+127 = 853+97 = 877+73 = 883+67 = 907+43 = 919+31 = 937+13 = 947+3 (# 50) 952 = 5+947 = 11+941 = 23+929 = 41+911 = 71+881 = 89+863 = 113+839 = 131+821 = 179+773 = 191+761 = 233+719 = 251+701 = 269+683 = 293+659 = 311+641 = 353+599 = 359+593 = 383+569 = 389+563 = 431+521 = 443+509 = 449+503 = 461+491 = 491+461 = 503+449 = 509+443 = 521+431 = 563+389 = 569+383 = 593+359 = 599+353 = 641+311 = 659+293 = 683+269 = 701+251 = 719+233 = 761+191 = 773+179 = 821+131 = 839+113 = 863+89 = 881+71 = 911+41 = 929+23 = 941+11 = 947+5 (# 46) 954 = 7+947 = 13+941 = 17+937 = 43+911 = 47+907 = 67+887 = 71+883 = 73+881 = 97+857 = 101+853 = 127+827 = 131+823 = 157+797 = 167+787 = 181+773 = 193+761 = 197+757 = 211+743 = 227+727 = 263+691 = 271+683 = 277+677 = 281+673 = 293+661 = 307+647 = 311+643 = 313+641 = 337+617 = 347+607 = 353+601 = 367+587 = 383+571 = 397+557 = 431+523 = 433+521 = 463+491 = 467+487 = 487+467 = 491+463 = 521+433 = 523+431 = 557+397 = 571+383 = 587+367 = 601+353 = 607+347 = 617+337 = 641+313 = 643+311 = 647+307 = 661+293 = 673+281 = 677+277 = 683+271 = 691+263 = 727+227 = 743+211 = 757+197 = 761+193 = 773+181 = 787+167 = 797+157 = 823+131 = 827+127 = 853+101 = 857+97 = 881+73 = 883+71 = 887+67 = 907+47 = 911+43 = 937+17 = 941+13 = 947+7 (# 74) 956 = 3+953 = 19+937 = 37+919 = 73+883 = 79+877 = 97+859 = 103+853 = 127+829 = 199+757 = 223+733 = 229+727 = 283+673 = 313+643 = 337+619 = 349+607 = 379+577 = 409+547 = 433+523 = 457+499 = 499+457 = 523+433 = 547+409 = 577+379 = 607+349 = 619+337 = 643+313 = 673+283 = 727+229 = 733+223 = 757+199 = 829+127 = 853+103 = 859+97 = 877+79 = 883+73 = 919+37 = 937+19 = 953+3 (# 38) 958 = 5+953 = 11+947 = 17+941 = 29+929 = 47+911 = 71+887 = 101+857 = 131+827 = 137+821 = 149+809 = 197+761 = 239+719 = 257+701 = 281+677 = 311+647 = 317+641 = 359+599 = 389+569 = 401+557 = 449+509 = 467+491 = 479+479 = 491+467 = 509+449 = 557+401 = 569+389 = 599+359 = 641+317 = 647+311 = 677+281 = 701+257 = 719+239 = 761+197 = 809+149 = 821+137 = 827+131 = 857+101 = 887+71 = 911+47 = 929+29 = 941+17 = 947+11 = 953+5 (# 43) 960 = 7+953 = 13+947 = 19+941 = 23+937 = 31+929 = 41+919 = 53+907 = 73+887 = 79+881 = 83+877 = 97+863 = 101+859 = 103+857 = 107+853 = 131+829 = 137+823 = 139+821 = 149+811 = 151+809 = 163+797 = 173+787 = 191+769 = 199+761 = 227+733 = 233+727 = 241+719 = 251+709 = 269+691 = 277+683 = 283+677 = 307+653 = 313+647 = 317+643 = 347+613 = 353+607 = 359+601 = 367+593 = 373+587 = 383+577 = 389+571 = 397+563 = 419+541 = 439+521 = 457+503 = 461+499 = 499+461 = 503+457 = 521+439 = 541+419 = 563+397 = 571+389 = 577+383 = 587+373 = 593+367 = 601+359 = 607+353 = 613+347 = 643+317 = 647+313 = 653+307 = 677+283 = 683+277 = 691+269 = 709+251 = 719+241 = 727+233 = 733+227 = 761+199 = 769+191 = 787+173 = 797+163 = 809+151 = 811+149 = 821+139 = 823+137 = 829+131 = 853+107 = 857+103 = 859+101 = 863+97 = 877+83 = 881+79 = 887+73 = 907+53 = 919+41 = 929+31 = 937+23 = 941+19 = 947+13 = 953+7 (# 90) 962 = 43+919 = 79+883 = 103+859 = 109+853 = 139+823 = 151+811 = 193+769 = 211+751 = 223+739 = 229+733 = 271+691 = 331+631 = 349+613 = 421+541 = 439+523 = 463+499 = 499+463 = 523+439 = 541+421 = 613+349 = 631+331 = 691+271 = 733+229 = 739+223 = 751+211 = 769+193 = 811+151 = 823+139 = 853+109 = 859+103 = 883+79 = 919+43 (# 32) 964 = 11+953 = 17+947 = 23+941 = 53+911 = 83+881 = 101+863 = 107+857 = 137+827 = 167+797 = 191+773 = 263+701 = 281+683 = 311+653 = 317+647 = 347+617 = 401+563 = 443+521 = 461+503 = 503+461 = 521+443 = 563+401 = 617+347 = 647+317 = 653+311 = 683+281 = 701+263 = 773+191 = 797+167 = 827+137 = 857+107 = 863+101 = 881+83 = 911+53 = 941+23 = 947+17 = 953+11 (# 36) 966 = 13+953 = 19+947 = 29+937 = 37+929 = 47+919 = 59+907 = 79+887 = 83+883 = 89+877 = 103+863 = 107+859 = 109+857 = 113+853 = 127+839 = 137+829 = 139+827 = 157+809 = 179+787 = 193+773 = 197+769 = 223+743 = 227+739 = 233+733 = 239+727 = 257+709 = 283+683 = 293+673 = 307+659 = 313+653 = 347+619 = 349+617 = 353+613 = 359+607 = 367+599 = 373+593 = 379+587 = 389+577 = 397+569 = 409+557 = 419+547 = 443+523 = 457+509 = 463+503 = 467+499 = 479+487 = 487+479 = 499+467 = 503+463 = 509+457 = 523+443 = 547+419 = 557+409 = 569+397 = 577+389 = 587+379 = 593+373 = 599+367 = 607+359 = 613+353 = 617+349 = 619+347 = 653+313 = 659+307 = 673+293 = 683+283 = 709+257 = 727+239 = 733+233 = 739+227 = 743+223 = 769+197 = 773+193 = 787+179 = 809+157 = 827+139 = 829+137 = 839+127 = 853+113 = 857+109 = 859+107 = 863+103 = 877+89 = 883+83 = 887+79 = 907+59 = 919+47 = 929+37 = 937+29 = 947+19 = 953+13 (# 90) 968 = 31+937 = 61+907 = 109+859 = 139+829 = 157+811 = 181+787 = 199+769 = 211+757 = 229+739 = 241+727 = 277+691 = 307+661 = 337+631 = 349+619 = 367+601 = 397+571 = 421+547 = 547+421 = 571+397 = 601+367 = 619+349 = 631+337 = 661+307 = 691+277 = 727+241 = 739+229 = 757+211 = 769+199 = 787+181 = 811+157 = 829+139 = 859+109 = 907+61 = 937+31 (# 34) 970 = 3+967 = 17+953 = 23+947 = 29+941 = 41+929 = 59+911 = 83+887 = 89+881 = 107+863 = 113+857 = 131+839 = 149+821 = 173+797 = 197+773 = 227+743 = 251+719 = 269+701 = 293+677 = 311+659 = 317+653 = 353+617 = 383+587 = 401+569 = 449+521 = 461+509 = 467+503 = 479+491 = 491+479 = 503+467 = 509+461 = 521+449 = 569+401 = 587+383 = 617+353 = 653+317 = 659+311 = 677+293 = 701+269 = 719+251 = 743+227 = 773+197 = 797+173 = 821+149 = 839+131 = 857+113 = 863+107 = 881+89 = 887+83 = 911+59 = 929+41 = 941+29 = 947+23 = 953+17 = 967+3 (# 54) 972 = 5+967 = 19+953 = 31+941 = 43+929 = 53+919 = 61+911 = 89+883 = 109+863 = 113+859 = 149+823 = 151+821 = 163+809 = 199+773 = 211+761 = 229+743 = 233+739 = 239+733 = 263+709 = 271+701 = 281+691 = 311+661 = 313+659 = 331+641 = 353+619 = 359+613 = 373+599 = 379+593 = 401+571 = 409+563 = 431+541 = 449+523 = 463+509 = 509+463 = 523+449 = 541+431 = 563+409 = 571+401 = 593+379 = 599+373 = 613+359 = 619+353 = 641+331 = 659+313 = 661+311 = 691+281 = 701+271 = 709+263 = 733+239 = 739+233 = 743+229 = 761+211 = 773+199 = 809+163 = 821+151 = 823+149 = 859+113 = 863+109 = 883+89 = 911+61 = 919+53 = 929+43 = 941+31 = 953+19 = 967+5 (# 64) 974 = 3+971 = 7+967 = 37+937 = 67+907 = 97+877 = 151+823 = 163+811 = 223+751 = 241+733 = 283+691 = 313+661 = 331+643 = 367+607 = 373+601 = 397+577 = 433+541 = 487+487 = 541+433 = 577+397 = 601+373 = 607+367 = 643+331 = 661+313 = 691+283 = 733+241 = 751+223 = 811+163 = 823+151 = 877+97 = 907+67 = 937+37 = 967+7 = 971+3 (# 33) 976 = 5+971 = 23+953 = 29+947 = 47+929 = 89+887 = 113+863 = 137+839 = 149+827 = 167+809 = 179+797 = 233+743 = 257+719 = 293+683 = 317+659 = 359+617 = 383+593 = 389+587 = 419+557 = 467+509 = 509+467 = 557+419 = 587+389 = 593+383 = 617+359 = 659+317 = 683+293 = 719+257 = 743+233 = 797+179 = 809+167 = 827+149 = 839+137 = 863+113 = 887+89 = 929+47 = 947+29 = 953+23 = 971+5 (# 38) 978 = 7+971 = 11+967 = 31+947 = 37+941 = 41+937 = 59+919 = 67+911 = 71+907 = 97+881 = 101+877 = 139+839 = 149+829 = 151+827 = 157+821 = 167+811 = 181+797 = 191+787 = 227+751 = 239+739 = 251+727 = 269+709 = 277+701 = 317+661 = 331+647 = 337+641 = 347+631 = 359+619 = 379+599 = 401+577 = 409+569 = 421+557 = 431+547 = 457+521 = 479+499 = 487+491 = 491+487 = 499+479 = 521+457 = 547+431 = 557+421 = 569+409 = 577+401 = 599+379 = 619+359 = 631+347 = 641+337 = 647+331 = 661+317 = 701+277 = 709+269 = 727+251 = 739+239 = 751+227 = 787+191 = 797+181 = 811+167 = 821+157 = 827+151 = 829+149 = 839+139 = 877+101 = 881+97 = 907+71 = 911+67 = 919+59 = 937+41 = 941+37 = 947+31 = 967+11 = 971+7 (# 70) 980 = 3+977 = 13+967 = 43+937 = 61+919 = 73+907 = 97+883 = 103+877 = 127+853 = 151+829 = 157+823 = 193+787 = 211+769 = 223+757 = 229+751 = 241+739 = 271+709 = 307+673 = 337+643 = 349+631 = 367+613 = 373+607 = 379+601 = 409+571 = 433+547 = 439+541 = 457+523 = 523+457 = 541+439 = 547+433 = 571+409 = 601+379 = 607+373 = 613+367 = 631+349 = 643+337 = 673+307 = 709+271 = 739+241 = 751+229 = 757+223 = 769+211 = 787+193 = 823+157 = 829+151 = 853+127 = 877+103 = 883+97 = 907+73 = 919+61 = 937+43 = 967+13 = 977+3 (# 52) 982 = 5+977 = 11+971 = 29+953 = 41+941 = 53+929 = 71+911 = 101+881 = 173+809 = 239+743 = 263+719 = 281+701 = 383+599 = 389+593 = 419+563 = 461+521 = 479+503 = 491+491 = 503+479 = 521+461 = 563+419 = 593+389 = 599+383 = 701+281 = 719+263 = 743+239 = 809+173 = 881+101 = 911+71 = 929+53 = 941+41 = 953+29 = 971+11 = 977+5 (# 33) 984 = 7+977 = 13+971 = 17+967 = 31+953 = 37+947 = 43+941 = 47+937 = 73+911 = 97+887 = 101+883 = 103+881 = 107+877 = 127+857 = 131+853 = 157+827 = 163+821 = 173+811 = 197+787 = 211+773 = 223+761 = 227+757 = 233+751 = 241+743 = 251+733 = 257+727 = 283+701 = 293+691 = 307+677 = 311+673 = 331+653 = 337+647 = 353+631 = 367+617 = 383+601 = 397+587 = 421+563 = 443+541 = 461+523 = 463+521 = 521+463 = 523+461 = 541+443 = 563+421 = 587+397 = 601+383 = 617+367 = 631+353 = 647+337 = 653+331 = 673+311 = 677+307 = 691+293 = 701+283 = 727+257 = 733+251 = 743+241 = 751+233 = 757+227 = 761+223 = 773+211 = 787+197 = 811+173 = 821+163 = 827+157 = 853+131 = 857+127 = 877+107 = 881+103 = 883+101 = 887+97 = 911+73 = 937+47 = 941+43 = 947+37 = 953+31 = 967+17 = 971+13 = 977+7 (# 78) 986 = 3+983 = 19+967 = 67+919 = 79+907 = 103+883 = 109+877 = 127+859 = 157+829 = 163+823 = 199+787 = 229+757 = 277+709 = 313+673 = 367+619 = 373+613 = 379+607 = 409+577 = 439+547 = 463+523 = 487+499 = 499+487 = 523+463 = 547+439 = 577+409 = 607+379 = 613+373 = 619+367 = 673+313 = 709+277 = 757+229 = 787+199 = 823+163 = 829+157 = 859+127 = 877+109 = 883+103 = 907+79 = 919+67 = 967+19 = 983+3 (# 40) 988 = 5+983 = 11+977 = 17+971 = 41+947 = 47+941 = 59+929 = 101+887 = 107+881 = 131+857 = 149+839 = 167+821 = 179+809 = 191+797 = 227+761 = 269+719 = 311+677 = 347+641 = 389+599 = 401+587 = 419+569 = 431+557 = 467+521 = 479+509 = 509+479 = 521+467 = 557+431 = 569+419 = 587+401 = 599+389 = 641+347 = 677+311 = 719+269 = 761+227 = 797+191 = 809+179 = 821+167 = 839+149 = 857+131 = 881+107 = 887+101 = 929+59 = 941+47 = 947+41 = 971+17 = 977+11 = 983+5 (# 46) 990 = 7+983 = 13+977 = 19+971 = 23+967 = 37+953 = 43+947 = 53+937 = 61+929 = 71+919 = 79+911 = 83+907 = 103+887 = 107+883 = 109+881 = 113+877 = 127+863 = 131+859 = 137+853 = 151+839 = 163+827 = 167+823 = 179+811 = 181+809 = 193+797 = 229+761 = 233+757 = 239+751 = 251+739 = 257+733 = 263+727 = 271+719 = 281+709 = 307+683 = 313+677 = 317+673 = 331+659 = 337+653 = 347+643 = 349+641 = 359+631 = 373+617 = 383+607 = 389+601 = 397+593 = 419+571 = 421+569 = 433+557 = 443+547 = 449+541 = 467+523 = 487+503 = 491+499 = 499+491 = 503+487 = 523+467 = 541+449 = 547+443 = 557+433 = 569+421 = 571+419 = 593+397 = 601+389 = 607+383 = 617+373 = 631+359 = 641+349 = 643+347 = 653+337 = 659+331 = 673+317 = 677+313 = 683+307 = 709+281 = 719+271 = 727+263 = 733+257 = 739+251 = 751+239 = 757+233 = 761+229 = 797+193 = 809+181 = 811+179 = 823+167 = 827+163 = 839+151 = 853+137 = 859+131 = 863+127 = 877+113 = 881+109 = 883+107 = 887+103 = 907+83 = 911+79 = 919+71 = 929+61 = 937+53 = 947+43 = 953+37 = 967+23 = 971+19 = 977+13 = 983+7 (# 104) 992 = 73+919 = 109+883 = 139+853 = 163+829 = 181+811 = 223+769 = 241+751 = 283+709 = 331+661 = 349+643 = 373+619 = 379+613 = 421+571 = 571+421 = 613+379 = 619+373 = 643+349 = 661+331 = 709+283 = 751+241 = 769+223 = 811+181 = 829+163 = 853+139 = 883+109 = 919+73 (# 26) 994 = 3+991 = 11+983 = 17+977 = 23+971 = 41+953 = 47+947 = 53+941 = 83+911 = 107+887 = 113+881 = 131+863 = 137+857 = 167+827 = 173+821 = 197+797 = 233+761 = 251+743 = 293+701 = 311+683 = 317+677 = 347+647 = 353+641 = 401+593 = 431+563 = 491+503 = 503+491 = 563+431 = 593+401 = 641+353 = 647+347 = 677+317 = 683+311 = 701+293 = 743+251 = 761+233 = 797+197 = 821+173 = 827+167 = 857+137 = 863+131 = 881+113 = 887+107 = 911+83 = 941+53 = 947+47 = 953+41 = 971+23 = 977+17 = 983+11 = 991+3 (# 50) 996 = 5+991 = 13+983 = 19+977 = 29+967 = 43+953 = 59+937 = 67+929 = 89+907 = 109+887 = 113+883 = 137+859 = 139+857 = 157+839 = 167+829 = 173+823 = 199+797 = 223+773 = 227+769 = 239+757 = 257+739 = 263+733 = 269+727 = 277+719 = 313+683 = 337+659 = 349+647 = 353+643 = 379+617 = 383+613 = 389+607 = 397+599 = 409+587 = 419+577 = 433+563 = 439+557 = 449+547 = 487+509 = 509+487 = 547+449 = 557+439 = 563+433 = 577+419 = 587+409 = 599+397 = 607+389 = 613+383 = 617+379 = 643+353 = 647+349 = 659+337 = 683+313 = 719+277 = 727+269 = 733+263 = 739+257 = 757+239 = 769+227 = 773+223 = 797+199 = 823+173 = 829+167 = 839+157 = 857+139 = 859+137 = 883+113 = 887+109 = 907+89 = 929+67 = 937+59 = 953+43 = 967+29 = 977+19 = 983+13 = 991+5 (# 74) 998 = 7+991 = 31+967 = 61+937 = 79+919 = 139+859 = 211+787 = 229+769 = 241+757 = 271+727 = 307+691 = 337+661 = 367+631 = 379+619 = 397+601 = 421+577 = 457+541 = 499+499 = 541+457 = 577+421 = 601+397 = 619+379 = 631+367 = 661+337 = 691+307 = 727+271 = 757+241 = 769+229 = 787+211 = 859+139 = 919+79 = 937+61 = 967+31 = 991+7 (# 33) 1000 = 3+997 = 17+983 = 23+977 = 29+971 = 47+953 = 53+947 = 59+941 = 71+929 = 89+911 = 113+887 = 137+863 = 173+827 = 179+821 = 191+809 = 227+773 = 239+761 = 257+743 = 281+719 = 317+683 = 347+653 = 353+647 = 359+641 = 383+617 = 401+599 = 431+569 = 443+557 = 479+521 = 491+509 = 509+491 = 521+479 = 557+443 = 569+431 = 599+401 = 617+383 = 641+359 = 647+353 = 653+347 = 683+317 = 719+281 = 743+257 = 761+239 = 773+227 = 809+191 = 821+179 = 827+173 = 863+137 = 887+113 = 911+89 = 929+71 = 941+59 = 947+53 = 953+47 = 971+29 = 977+23 = 983+17 = 997+3 (# 56)