Let's see some unfortunate consequences of that when using floating point numbers
during computations.
Mathematically speaking, floating point numbers are not numbers for the properties
of associativity and distributivity are lost. Let's recall the respective meanings of these properties:
(AxB)xC = Ax(BxC)
(A+B)+C = A+(B+C)
Ax(B+C) = AxB+AxC
for any triplet of numbers 'A', 'B' and 'C'. Let's check that regarding the associativity
running the two following small programs:
double addition(x,y) double multiplication(x,y)
double x; double x;
double y; double y;
{ {
return(x+y); return(x*y);
} }
main() main()
{ {
double a=1.1; double a=1.5;
double b=3.7; double b=2.3;
double c=5.5; double c=3.7;
double x1,x2; double x1,x2;
x1 = addition(addition(a,b),c); x1 = multiplication(multiplication(a,b),c);
x2 = addition(a,addition(b,c)); x2 = multiplication(a,multiplication(b,c));
printf("(%.6f + %.6f) + %.6f = %.15f\n",a,b,c,x1); printf("(%.6f * %.6f) * %.6f = %.15f\n",a,b,c,x1);
printf("%.6f + (%.6f + %.6f) = %.15f\n",a,b,c,x2); printf("%.6f * (%.6f * %.6f) = %.15f\n",a,b,c,x2);
} }
(1.100000 + 3.700000) + 5.500000 = 10.300000000000001 (1.500000 * 2.300000) * 3.700000 = 12.764999999999999
1.100000 + (3.700000 + 5.500000) = 10.299999999999999 1.500000 * (2.300000 * 3.700000) = 12.765000000000001
It is noteworthy that two functions are used to compute the addition and the multiplication respectively
in order to force the respect of the order of the operations.
The results obtained are different but after all the differences are very small. But are the things always
so clean? Let's run this small program (for the sake of simplicity an iteration is not used):
main()
{
double A,B,x0,x1,x2,x3,x4,x5,x6,x7;
B=4095.1;
A=B+1;
x0 = 1;
x1 = (A*x0) - B;
x2 = (A*x1) - B;
x3 = (A*x2) - B;
x4 = (A*x3) - B;
x5 = (A*x4) - B;
x6 = (A*x5) - B;
x7 = (A*x6) - B;
printf("x0 = %+.16f\n",x0);
printf("x1 = %+.16f\n",x1);
printf("x2 = %+.16f\n",x2);
printf("x3 = %+.16f\n",x3);
printf("x4 = %+.16f\n",x4);
printf("x5 = %+.16f\n",x5);
printf("x6 = %+.16f\n",x6);
printf("x7 = %+.16f\n",x7);
}
x0 = +1.0000000000000000
x1 = +1.0000000000004547
x2 = +1.0000000018630999
x3 = +1.0000076314440776
x4 = +1.0312591580864137
x5 = +129.0406374377594148
x6 = +524468.2550088063580915
x7 = +2148270324.2415719032287598
It is noteworthy that this very simplistic program does not contain bugs,
does not use approximation methods and at last its answers (=1) are known a priori
(that is unique!).
As a matter of fact the following property is true:
A=B+1 ==> A-B=1 ==> x7=x6=x5=x4=x3=x2=x1=x0=1
Unfortunately this program does not give values equal to 1 (except the first one obviously).
Where is the problem?
In fact, A-B does not equal to 1; it is equal to 1 plus/minus epsilon (one single bit)
for 4095.1 and 4096.1 cannot be defined accurately inside a computer using floating point numbers.
Obviously this phenomenon is independent of the programming language used
as can be seen with the
Fortran 95
or again the Python
versions of this program.
This program is more than interesting for on the one hand it exhibits clearly a general
problem of computer accuracy.
On the other hand, it gives an example of an "explosive" process with the
fast expansion of a very smal error (the preceding single bit).
At last, it makes use of a process
known as iterative computation where values are transformed
and transformed again following certain laws.
It will be the case with the last example with
the tridimensional coordinates of the four bodies (two stars and two planets). As a matter
of fact, those coordinates will be defined a priori at
the start of the computation and then transformed iteratively using the newtonian
laws of classical Physics.
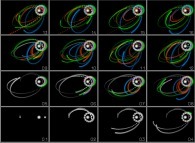
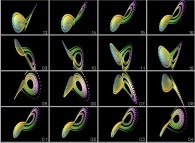 Then a single program running on several different computers could produce non identical results
Then a single program running on several different computers could produce non identical results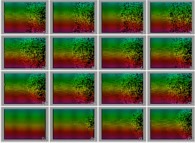 can lost their property of reversibility
can lost their property of reversibility