Un peu d'histoire des Mathématiques et de ses révolutions :
Quelle est la forme (au sens mathématique du terme...) d'un nuage ?
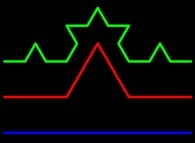
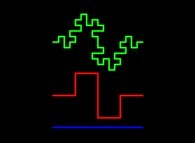
Au XIXe siècle, du continu 
différentiable 
au continu non différentiable :
Les "monstres" de Weierstrass, Cantor, Peano, von Koch, Sierpinski,... était pour Charles Hermite une plaie lamentable qu'il regardait avec effroi.
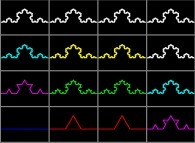
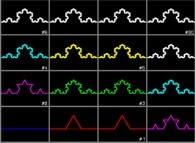
Seules des approximations peuvent être présentées, ce qui n'a rien d'exceptionnel, les décimales de π en étant le meilleur exemple...
Deux propriétés extraordinaires :
Les courbes remplissantes :
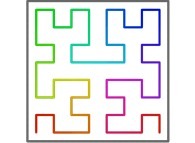
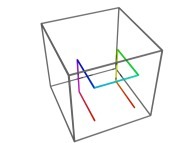
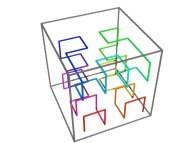
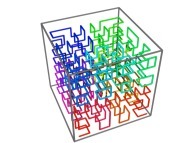
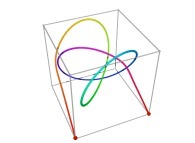
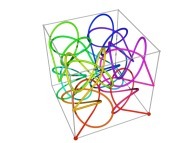
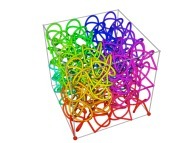
Au XXe siècle, de Benoît Mandelbrot à l'Universalité des fractales (Bernard Sapoval) :
Dans la deuxième moitié du XXe siècle, l'ordinateur a joué un rôle important dans l'émergence de la Géométrie Fractale :
Les objets fractals possédent de l'irrégularité et/ou des structures à tous les niveaux et/ou une dimension non entière.
Formes naturelles et autosimilarité :
Formes naturelles et infini (les contraintes de la Nature) :
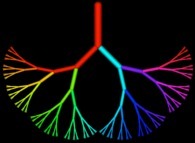
La dimension fractale, une mesure de l'irrégularité :
Soit K un cube
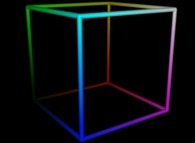de côté C (supposé entier et strictement supérieur à 1 pour simplifier).
Son volume V est défini par :
 | |
| V = C3 | 125 = 53 |
| || \/ | || \/ |
| log(V) = 3 * log(C) | log(125) = 3 * log(5) |
| || \/ | || \/ |
| 3 = log(V) / log(C) | 3 = log(125) / log(5) |
Mais :
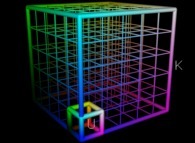
- V est aussi le nombre N de cubes unité U contenu dans K (ou nombre de copies),
- C est aussi le rapport d'homothétie H permettant de passer de U à K,
- 3 est aussi la dimension D de K.
d'où :
| D = log(V) / log(C) |
| || \/ |
| D = log(N) / log(H) |
Cette définition de D peut-être étendue à tout objet et D est alors appelée dimension fractale.
Dans le cas de la courbe de von Koch :
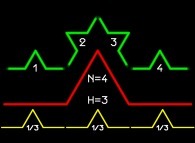
N=4 (=nombre de copies)
H=3 (=rapport d'homothétie)
et ainsi :
D = log(4) / log(3)
1 < log(4)/log(3) = 1.261859507142915 < 2 ==> "droite < courbe de von Koch < plan"
Quelques exemples d'objets classés par ordre de dimensions fractales croissantes :
 0 : un point. |  log(2)/log(3)=0.63... : l'ensemble triadique de Cantor. |
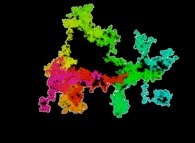
 2: le mouvement brownien bidimensionnel -en couleurs-. |  2 : courbe de Hilbert bidimensionnelle. |  2 : un plan. |  log(20)/log(3)=2.72... : l'éponge de Menger. |
 3 : courbe de Hilbert tridimensionnelle. |  3 : l'espace tridimensionnel. |
 4 : l'hypercube. |
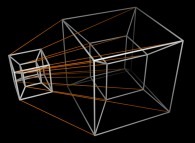 5 : l'hyperhypercube. |
 11 : l'espace-temps à l'échelle de Planck (10-35 mètre et 10-43 seconde) ? |
L'Emergence des Fractales (de l'intérêt des images !) :
- En Mathématiques :
- En Physique :
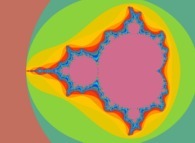
La Géométrie Fractale déterministe (Gaston Julia, Pierre Fatou, Benoît Mandelbrot, Adrien Douady, John Hubbard, Jean-Christophe Yoccoz,... XXe siècle) :
La Géométrie Fractale non déterministe (Benoît Mandelbrot ~1960) :
Les difficultés et les problèmes [voir en particulier ce calcul édifiant] :
Demain : du continu non différentiable au NON CONTINU NON DIFFÉRENTIABLE ?
- Les raisons de l'omniprésence des nombres réels en Physique.
- Le problème des erreurs d'arrondi dans nos ordinateurs.
Les fractales et l'art :
[Plus d'informations sur Arts et Mathématiques, Mathématiques et Arts]
La Réalité (et la Science donc...) serait-elle la Fractale Ultime?
Souvenons-nous des annonces de Lord Kelvin à la fin du XIXe siècle, quelques années avant la Mécanique Quantique et les Relativités -Restreinte et Générale- : Il n'y a plus rien à découvrir en physique aujourd'hui, tout ce qui reste est d'améliorer la précision des mesures...En résumé :
- La Géométrie Fractale est un langage commun qui unifie en quelque sorte :
- Les probabilités,
- Les itérations,
Les interfaces.
- La Géométrie Fractale introduit une nouvelle invariance :
- L'invariance d'échelle
à côté de :
- L'invariance par translation dans l'espace -conservation de la quantité de mouvement-,
- L'invariance par translation dans le temps -conservation de l'énergie-,
- L'invariance par rotation -conservation du moment cinétique-.
- Une propriété fondamentale des objets fractals :
La cohabitation de mesures à la fois finie et infinie que cette géométrie permet (ce qu'illustre parfaitement notre système respiratoire...). Et c'est certainement l'explication de son
omniprésence dans la nature. On pourrait donc, pour plaisanter,
compléter l'affirmation d'Albert Einstein "Dieu ne joue pas aux dés",
en ajoutant "mais il fait certainement de la Géométrie Fractale"...
