The abelian -commutative- group defined on elliptic curves [Le groupe abélien -commutatif- défini sur les courbes elliptiques].
[See the so-called last Fermat's theorem]
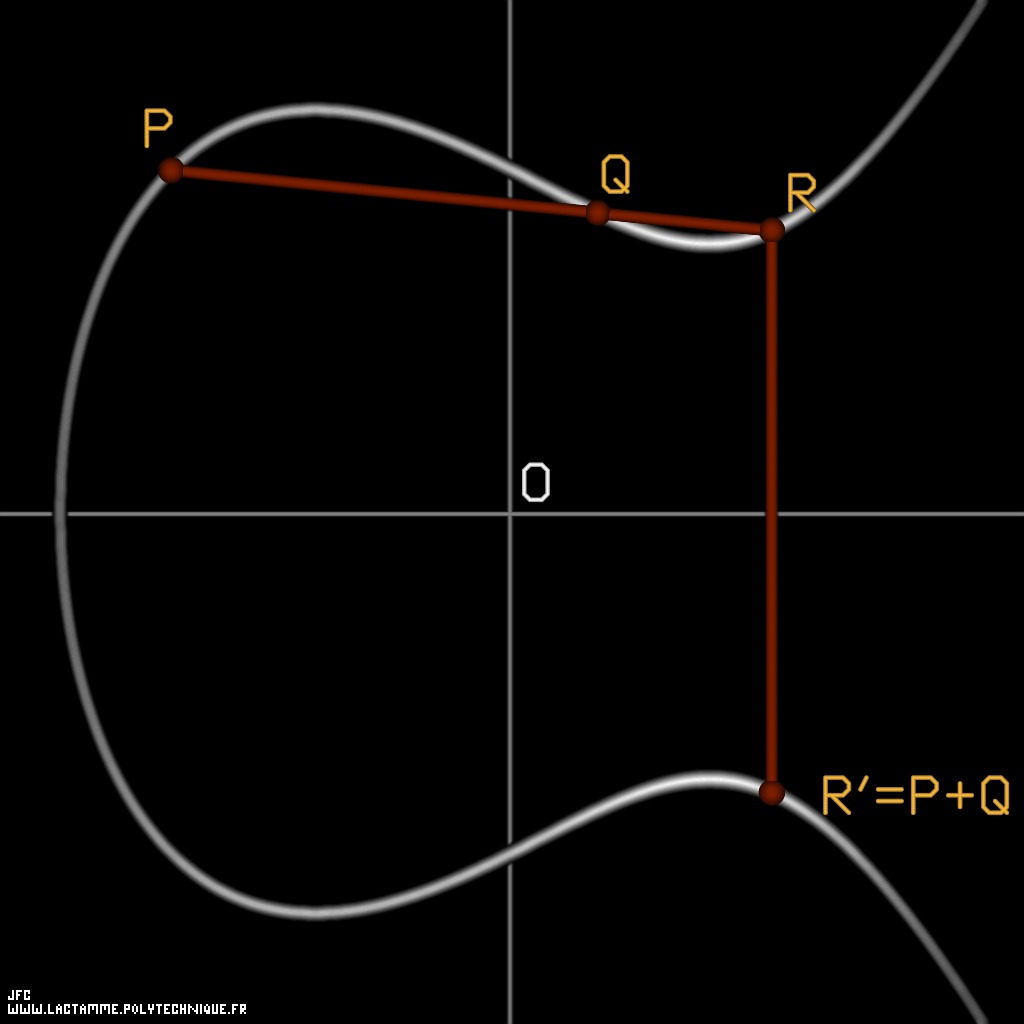
The continuous white line displays the following elliptic curve:
y2 = x3 - x + 1
An elliptic curve is an abelian -i.e. commutative- group:
- Definitions:
- I (the identity of the group) is the point at infinity (a vertical line on the picture).
- The inverse of a point A=A(x,y) is -A=A(x,-y). On the picture C' means -C and defines A+B.
- A+B+C = I
- Abelian group laws:
- A+I = I+A = A [Identity]
- A+(-A) = (-A)+A = I [Inverse]
- (A+B)+C = A+(B+C) [Associativity]
- A+B = B+A [Commutativity]
On this picture, the 3 points A, B and C have rational coordinates:
1 1
A = {- --- , + ---}
1 1
1 7
B = {+ --- , + ---}
4 8
19 103
C = {+ ---- , + -----}
25 125
(CMAP28 WWW site: this page was created on 09/18/2013 and last updated on 07/11/2025 17:13:30 -CEST-)
[See the generator of this picture [Voir le générateur de cette image]]
[See all related pictures (including this one) [Voir toutes les images associées (incluant celle-ci)]]
[Please visit the related ImagesDidactiques picture gallery [Visitez la galerie d'images ImagesDidactiques associée]]
[Please visit the related NumberTheory picture gallery [Visitez la galerie d'images NumberTheory associée]]
[Go back to AVirtualMachineForExploringSpaceTimeAndBeyond [Retour à AVirtualMachineForExploringSpaceTimeAndBeyond]]
[The Y2K Bug [Le bug de l'an 2000]]
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[Mail [Courrier]]
[About Pictures and Animations [A Propos des Images et des Animations]]
Copyright © Jean-François COLONNA, 2013-2025.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2013-2025.

