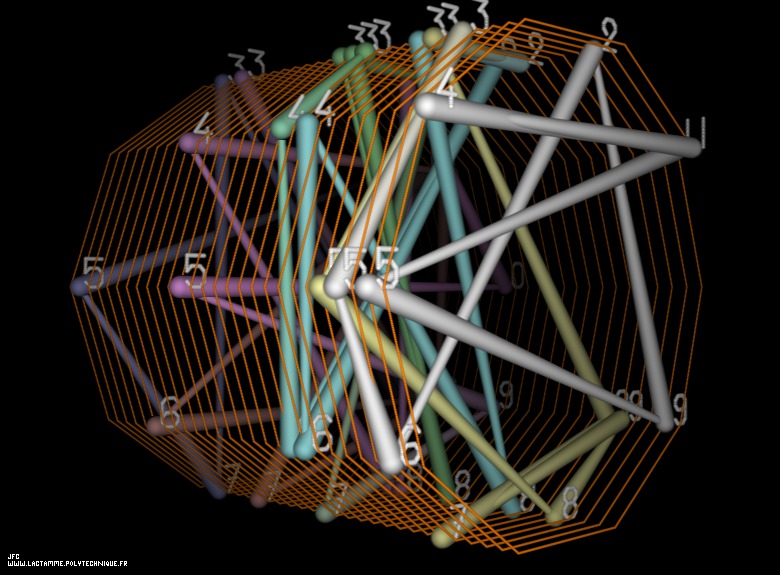
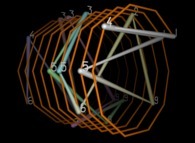
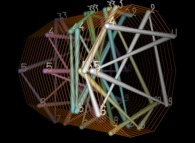
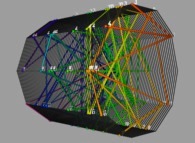
The 50 first digits {141592...} of 'pi' displayed on an helix -orange- [Les 50 premières décimales {141592...} de 'pi' visualisées sur une hélice -orange-].




To each digit D inside [0,9] is associated an angle A(D) with the following rule: 
                    A(D) = D.(2.pi/10)
Then each digit D(n) (n ∈ [1,...]) is displayed as a point (belonging to an helix) with the following tridimensional coordinates: 
                    X = cos(A(D(n)))
                    Y = sin(A(D(n)))
                    Z = f(n)
'f' denoting an "arbitrary" function.

At last, the current picture displays all the segments {D(n),D(n+1)} (for n=1 to 999).


See some related pictures (including this one) displaying one circle -left-hand side picture- and two helices -midle and right-hand side pictures-:



The left-hand side picture -using a parallel projection, hence a circle-like structure- seems to exhibit extraordinary symmetries, when the right-hand side one shows that there are none. Obviously, those apparent symmetries are due to the fact that 'pi' is a normal number (not yet demonstrated -in 2019-) meaning that, for example, the frequencies of 00, 01, 02,..., 97, 98, 99 are equal (and equal to 1/100). Thus, whatever the digits p and q, one can find n such as D(n)=p and D(n+1)=q. Then all segments p ==> q must exist if a sufficient number of digits of 'pi' is computed (1000 for this picture -in fact 850 would be sufficient-)...


See the helix and the 20, 50 and 100 first digits:




[See the 100.000 first digits -base 10- of 'pi'.]
[Plus d'informations à ce sujet -en français/in french-]


See some related pictures (including this one):


pi.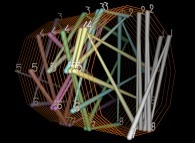
e.
The Golden Ratio.
The square root of 2.
Champernowne number.


[More pictures about these great mathematical constants]-


(CMAP28 WWW site: this page was created on 09/04/2020 and last updated on 09/05/2024 14:17:15 -CEST-)



[See the generator of this picture [Voir le générateur de cette image]]

[See all related pictures (including this one) [Voir toutes les images associées (incluant celle-ci)]]

[Please visit the related NumberTheory picture gallery [Visitez la galerie d'images NumberTheory associée]]

[Go back to AVirtualMachineForExploringSpaceTimeAndBeyond [Retour à AVirtualMachineForExploringSpaceTimeAndBeyond]]

[The Y2K Bug [Le bug de l'an 2000]]

[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[Mail [Courrier]]
[About Pictures and Animations [A Propos des Images et des Animations]]


Copyright © Jean-François COLONNA, 2020-2024.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2020-2024.