La Conjecture de Proth-Gilbreath
Battre le record de Andrew Odlyzko G(Pi(1013))=635 (1993)
G(Pi(1014))=693 le 05/10/2025 à 20:59:18
G(Pi(2.8000*1014))=788 le 08/11/2025 à 17:46:01
G(Pi(6.1500*1014))=800 le 13/12/2025 à 17:24:56
G(Pi(1015))=800 le 23/01/2026 à 18:41:08
G(Pi(1.0025*1015))=806 le 24/01/2026 à 00:51:08
G(Pi(1.2075*1015))=809 le 15/02/2026 à 02:58:42
G(Pi(1.2125*1015))=811 le 15/02/2026 à 21:50:58
Vérification jusqu'à 1.5x1015
CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[Real Numbers don't exist in Computers and Floating Point Computations aren't safe. [Les Nombres Réels n'existent pas dans les Ordinateurs et les Calculs Flottants ne sont pas sûrs.]]
[N'oubliez pas de visiter Une Machine Virtuelle à Explorer l'Espace-Temps et au-delà où vous trouverez plus de 10.000 images et animations à la frontière de l'Art et de la Science]
(Site WWW CMAP28 : cette page a été créée le 28/09/2025 et mise à jour le 18/03/2026 14:26:47 -CET-)
[in english/en anglais]
Remarque préliminaire :
Ce qui suit résulte d'une collaboration avec Jean-Paul Delahaye professeur émérite à l'Université de Lille,
chercheur au Laboratoire Cristal de Lille et chroniqueur bien connu de Pour La Science.
Contenu :
1-Introduction :
Une conjecture est
une proposition mathématique que l'on croit être vraie mais que l'on ne peut qualifier
de théorème
tant que toute tentative de démonstration a échoué...
Le plus bel exemple récent fut la démonstration du grand théorème de Fermat par Andrew Wiles en 1994
alors qu'il résistait aux plus grands mathématiciens depuis le XVIIe siècle.
Beaucoup de conjectures importantes sont actuellement "en attente". C'est ainsi le cas de
la conjecture de Goldbach -CG-
ou encore de celle des nombres premiers jumeaux -CNPJ-.
Pour une conjecture donnée, tant qu'une démonstration correcte n'a pas été trouvée, il est possible de tenter de
l'infirmer par la mise en évidence d'un contre-exemple, lorsque cela a un sens. Cela ne serait pas le cas pour CNPJ
car en effet ne plus voir de couples de nombres premiers jumeaux ne prouverait en aucune façon qu'en poursuivant beaucoup plus longtemps cette recherche,
de nouveaux couples n'apparaitraient pas. Par contre, pour CG découvrir un nombre pair supérieur à 2 qui ne serait pas la somme de deux
nombres premiers prouverait évidemment que CG est fausse. Malheureusement, s'il en existe un, la probabilité pour qu'il nous soit accessible est
quasiment nulle (en fait, tous les nombres entiers sont énormes, voire inimaginables,
sauf évidemment les premiers : ceux que l'on utilise dans la vie courante...).
Mais même si cette recherche de contre-exemple peut parfois paraître vaine, elle peut malgé tout être utile
en nous révélant des informations pertinentes relatives à un certain sujet et c'est le cas de conjecture de Gilbreath et des nombres premiers...
2-Définition :
Il s'agit d'une conjecture énoncée en 1958 par Norman L. Gilbreath [02] mais déjà formulée en 1878 par François Proth [03].
Elle est relative aux nombre premiers et aux séquences obtenues en calculant la valeur absolue de la différence
entre chaque nombre premier et son successeur,
puis en répétant ce processus ad infinitum [04] :
2 3 5 7 11 13 17 19 23 29 31 (...) <-- nombres premiers
\ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ /
1 2 2 4 2 4 2 4 6 2 (...) <-- écart entre nombres premiers
\ / \ / \ / \ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ / \ / \ / \ /
1 0 2 2 2 2 2 2 4 (...)
\ / \ / \ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ / \ / \ /
1 2 0 0 0 0 0 2 (...)
\ / \ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ / \ /
1 2 0 0 0 0 2 (...)
\ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ /
1 2 0 0 0 2 (...)
\ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ /
1 2 0 0 2 (...)
\ / \ / \ / \ / \ /
\ / \ / \ / \ / \ /
\ / \ / \ / \ / \ /
\ / \ / \ / \ / \ /
1 2 0 2 (...)
\ / \ / \ / \ /
\ / \ / \ / \ /
\ / \ / \ / \ /
\ / \ / \ / \ /
1 2 2 (...)
\ / \ / \ /
\ / \ / \ /
\ / \ / \ /
\ / \ / \ /
1 0 (...)
\ / \ /
\ / \ /
\ / \ /
\ / \ /
1 (...)
\ /
\ /
\ /
\ /
(...)
Cette conjecture qui affirme que la première valeur de chaque ligne est un 1 (à l'exception de la première ligne où il s'agit d'un 2 -le premier nombre premier-)
a été étudiée en 1993 par Andrew Odlyzko. Il avait pu alors la vérifier pour tous les nombres premiers inférieurs à 1013.
Le dimanche 05/10/2025 à 20:45 (heure de Paris, France) j'ai réussi à la vérifier jusqu'à 1014
et le mardi 07/10/2025 à 02:25 pm (East Time), Simon Plouffe (Canada) atteignait lui aussi cette valeur confirmant en même temps la valeur maximale (693)
de la fonction G(Pi(x)) [05] avec x ∈ [2,1014]
que j'avais anticipée le 25/09/2025.
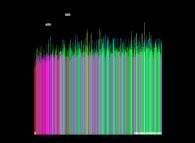
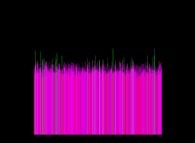
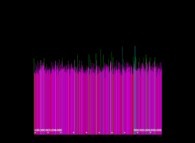
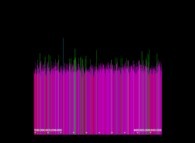
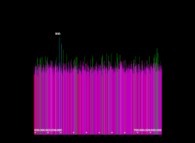
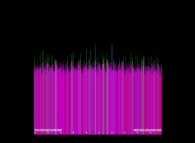
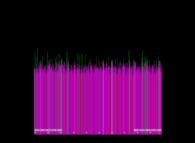
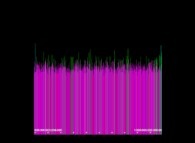
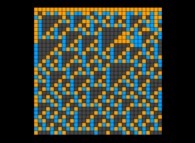
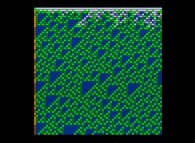
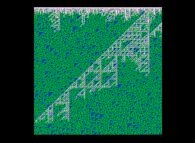
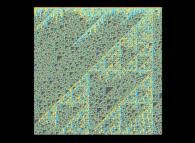
Voici quelques visualisations de ce processus incluant quelques records absolus
(première colonne (gauche) : les signes des différences, deuxième colonne : la valeur absolue des différences et troisième colonne : les différences) :
x 
= 
x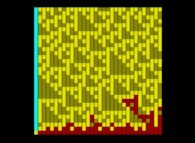 
= 
x 
= 
x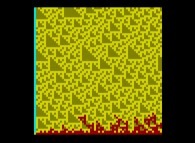 
= 
x 
= 
x 
= 
G(Pi(6.1500x1014))=800 -record absolu-
x 
= 
G(Pi(1.0025x1015))=806 -record absolu-
x 
= 
G(Pi(1.2075x1015))=809 -record absolu-
x 
= 
G(Pi(1.2125x1015))=811 -record absolu-
avec les conventions suivantes pour le coloriage des nombres sur les images de la troisième colonne :
0 = cyan foncé,
-1 = orange sombre,
+1 = orange clair,
-2 = vert sombre,
+2 = vert clair,
alors que tous les autres nombres -{3,4,5,6,7,8,...}- sont gris (gris sombre et clair respectivement pour les nombres négatifs et positifs).
Lorsque le premier nombre premier utilisé est 2, d'après la Conjecture de Proth-Gilbreath, dans les images du milieu, la colonne de gauche doit être cyan ('1')
à l'exception du carré situé tout en haut qui est jaune vif ('2', le premier nombre premier).
On remarquera que les carrés jaunes définissent des automates cellulaires binaires monodimensionnels.
Voici quelques autres visualisations de ce processus avec éventuellement des records relatifs :
G(Pi(1.6931x1015))=969 -record relatif-
G(Pi(6.0213x1027))=1935 -record relatif-
3-La théorie :
Il n'est évidemment pas possible de vérifier la Conjecture de Proth-Gilbreath puisqu'il y a une infinité de nombres premiers.
Seule une démonstration peut en venir à bout, à moins de trouver un contre-exemple, c'est-à-dire une ligne ne commençant pas par un '1'
(à l'exception de la première évidemment).
Soient pn les nombres premiers :
p1=2
p2=3
p3=5
etc...
Définissons la suite dk(n) :
d0(n) = pn pour tout n tel que n > 0
dk(n) = |dk-1(n) - dk-1(n+1)| pour tout k tel que k > 0 et pour tout n tel que n > 0
Il faut donc vérifier que :
dk(1) = 1 pour tout k tel que k > 0
Mais si cela doit être vérifié de façon exhaustive, rapidement le nombre de calculs à effectuer, ainsi
que la mémoire nécessaire dépassent la capacité des ordinateurs. Fort heureusement Andrew Odlyzko remarqua que si pour un certain N il existe K tel que :
dK(1) = 1
dK(n) ∈ {0,2} pour tout n tel que 0 < n < N+1
alors :
dk(1) = 1 pour tout k tel que K-1 < k < N+K
Appelons G(N) le plus petit k (s'il existe) tel que :
dj(1) = 1, 0 < j < k+1
dk(n) ∈ {0,2} pour tout n tel que 0 < n < N+1
Un raisonnement trivial montre que G(N) existe pour tout N et que l'on peut arrêter le processus dès qu'il n'y a plus que des '0's, des '1's et des '2's sur la ligne de rang k courante.
Par exemple :
k=0 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71
≠ ≠ ≠ ≠≠ ≠≠ ≠≠ ≠≠ ≠≠ ≠≠ ≠≠ ≠≠ ≠≠ ≠≠ ≠≠ ≠≠ ≠≠ ≠≠ ≠≠ ≠≠
k=1 1 2 2 4 2 4 2 4 6 2 6 4 2 4 6 6 2 6 4
≠ ≠ ≠ ≠ ≠ ≠ ≠ ≠ ≠ ≠ ≠
k=2 1 0 2 2 2 2 2 2 4 4 2 2 2 2 0 4 4 2
≠ ≠ ≠ ≠
k=3 1 2 0 0 0 0 0 2 0 2 0 0 0 2 4 0 2
≠
k=4 1 2 0 0 0 0 2 2 2 2 0 0 2 2 4 2
≠
k=5 1 2 0 0 0 2 0 0 0 2 0 2 0 2 2
==> G=5
4-Le calcul :
En 1993 Andrew Odlyzko vérifiait cela pour tous les nombres premiers inférieurs à 1013.
Le dimanche 10/08/2025, Jean-Paul Delahaye me proposait "un beau calcul", non trivial, mais semble-t-il faisable : il
s'agissait d'aller au-delà de 1013 et d'atteindre par exemple 1014...
Sur le papier, la chose est simple : il suffit de s'inspirer de l'exemple ci-dessus, mais au lieu de s'arréter à 71 il convient de dépasser 1013.
Il est évident que les ordinateurs ne peuvent ni mémoriser et ni manipuler une telle quantité de nombres.
L'idée est donc de travailler par blocs traités successivement et de tailles compatibles avec les machines utilisées. Mais ce découpage ne peut pas
se faire naïvement comme on peut le voir en decoupant l'exemple précédent en 2 blocs :
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71
1 2 2 4 2 4 2 4 6 6 4 2 4 6 6 2 6 4
1 0 2 2 2 2 2 2 2 2 2 2 0 4 4 2
0 0 0 2 4 0 2
0 0 2 2 4 2
0 2 0 2 2
De toute évidence, il manque la différence 31-29. Jean-Paul Delahaye a alors suggéré que les blocs ne soient
pas disjoints, mais se recouvrent partiellement comme suit en fonction d'un G estimé (à 5 ci-dessous) :
2 3 5 7 11 13 17 19 23 29 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71
1 2 2 4 2 4 2 4 6 4 2 4 6 2 6 4 2 4 6 6 2 6 4
1 0 2 2 2 2 2 2 2 2 2 4 4 2 2 2 2 0 4 4 2
1 2 0 0 0 0 0 0 0 2 0 2 0 0 0 2 4 0 2
1 2 0 0 0 0 0 2 2 2 2 0 0 2 2 4 2
1 2 0 0 0 2 0 0 0 2 0 2 0 2 2
soit :
2 3 5 7 11 13 17 19 23 29
13 17 19 23 29 31 37 41 43 47 53 59 61 67 71
== == == == ==
1 2 2 4 2 4 2 4 6
4 2 4 6 2 6 4 2 4 6 6 2 6 4
= = = =
1 0 2 2 2 2 2 2
2 2 2 4 4 2 2 2 2 0 4 4 2
= = =
1 2 0 0 0 0 0
0 0 2 0 2 0 0 0 2 4 0 2
= =
1 2 0 0 0 0
0 2 2 2 2 0 0 2 2 4 2
=
1 2 0 0 0
2 0 0 0 2 0 2 0 2 2
On pourrait remarquer que ce recouvrement de 5 nombres augmente de façon significative le nombre de calculs. En fait c'est vrai sur cet exemple
où chaque bloc ne contient que 10 nombres. Mais les calculs qui seront faits pour battre le record de 1993 utiliseront des blocs
beaucoup plus gros (en général 107) et même si le recouvrement utilisé est plus important (en général de l'ordre de 1000),
le nombre de calculs supplémentaires dus aux recouvrements est relativement très faible.
En ce qui concerne la taille des recouvrements ce sont les résultats publiés en 1993 par Andrew Odlyzko qui ont guidé son choix :
x Pi(x) G(Pi(x))
102 25 5
103 168 15
104 1229 35
105 9592 65
106 78498 95
107 664579 135
108 5761455 175
109 50847534 248
1010 455052511 329
1011 4118054813 417
1012 37607912018 481
1013 346065536839 635
où 'x' est le dernier nombre entier testé (quant au dernier nombre premier il est strictement inférieur à x),
'Pi(x)' est le nombre de nombres premiers dans [1,x] et enfin 'G(Pi(x))' nous donne la taille minimale des recouvrements.
L'architecture matérielle :
Six ordinateurs sont utilisés [06] : d'une part cinq serveurs de calcul ("C") assurant les calculs proprement dits et d'autre part
un PC dit "Superviseur" ("S") qui assure la répartition des différents calculs sur les serveurs. Toutes ces machines
sont sous Linux et sont raccordées à un serveur de fichiers NFS. Voici les configurations donnant dans l'ordre le nombre maximal de
processeurs [07], la capacité mémoire en Go [08] et enfin un indice de performance [09] :
- C1: {40,263,1}
- C2: {12,198,1.3875}
- C3: {12,148,1.48375}
- C4: {16,131,1.52857}
- C5: {36,528,1.6411}
Les programmes :
Un ensemble de programmes destines à tourner sur des ordinateurs sous Linux ont été écrits :
- Un programme de base P1 en C qui sera exécuté en parallèle sur tous les processeurs utiles des serveurs de calcul et
qui reçoit les arguments suivants :
- Le premier nombre entier PNE à tester (non nécessairement premier).
- Le dernier nombre entier DNE à tester (non nécessairement premier).
- Le nombre de blocs NB définissant le découpage de l'intervalle [PNE,DNE]
- Le nombre de nombres premiers NPP définissant le recouvrement inter-blocs.
- Quelques arguments complémentaires destinés à suivre en particulier la progression du calcul.
Ce programme définit la fonction primordiale 'NextPrime(n)' qui renvoie le premier nombre premier qui suive strictement le nombre 'n'
en utilissnt les tests de primalité de Miller-Rabin rendus déterministes.
Une boucle principale génère les NB blocs
de l'intervalle [PNE,DNE] en intégrant évidemment le recouvrement, puis une boucle interne balaye successivement chacun de ces NB blocs
afin de calculer les différences définissant le processus. A priori cette boucle est répétée NNP fois,
mais en fait une optimisation fait qu'elle est interrompue dès que n'apparaissent plus que des '0's, des '1's ou des '2's.
A un instant donné, toutes les occurences de P1 sur les différents serveurs Ci seront exécutées avec
la priorité la plus basse [10] ce qui, associé à la très faible "consommation" mémoire [08],
minimise la gène causée aux éventuels autres utilisateurs.
- Un script P2 en Cshell qui est exécuté sur S et qui distribue équitablement les calculs à effectuer à raison
d'un bloc par processeur, puis attend que tous les blocs aient été calculés.
Il s'agit là d'une allocation statique des blocs aux processeurs. Mais étant donné que tous les blocs ne demandent
pas le même temps de calcul [11], il est évident qu'une allocation dynamique aurait été préférable.
Pour ce faire, il aurait suffit de créer des blocs plus petits mais plus nombreux, puis de les placer dans une file d'attente.
Ensuite, dès qu'un processeur quelconque aurait été libre, il aurait prélevé le bloc de tête et ce jusqu'à ce
que la file soit vide. Mais étant donné qu'il y a plusieurs serveurs de calcul différents, cette file d'attente aurait du être
un fichier partagé NFS. Or malheureusement, même lorsqu'un serveur NFS est configuré comme il le faut, l'exclusion des
phases critiques de mise à jour d'un fichier partagé n'est pas fiable à 100% : les expériences faites l'ont montré et ont donc
contraint à implémenter l'allocation statique [12]...
- Un script P3 en Cshell qui est exécuté sur S et qui découpe le calcul complet en sous-calculs soumis à P2
et qui ne demanderont chacun qu'environ cinq heures. Cela permet d'interrompre le calcul complet (volontairement ou en cas de défauts matériels) et de le
reprendre en n'ayant perdu que quelques heures, mais sans voir disparaitre des informations utiles.
P3 permet de plus de répartir dans le temps le lancement des différents P2's : c'est ainsi que, pour le record du 05/10/2025,
les calculs n'ont eu lieu que durant les week-ends et la nuit en semaine.
5-Les résultats :
Les premiers calculs ont commencé le samedi 20/09/2025 à 11:14:28 puis ont été interrompus plusieurs jours à
cause de l'indisponibilité des serveurs de calcul.
Le calcul définitif s'est terminé [13] le dimanche 05/10/2025 à 20:59:18 (heure de Paris, France) comme je l'ai
signalé dans un mail à Jean-Paul Delahaye à 22:36:20 lui indiquant la fin de la dernière étape (qui concernait les nombres premiers de
75.000.000.000.000 à 100.000.000.000.000). Et cela confirmait un mail que je lui avais adressé le 25/09/2025 à 07:17:47 :
Bonne nouvelle : G(Pi(2x1013))=693
qui montrait que G(Pi(1014)) serait supérieure ou égale à 693. Le 05/10/2025 à 20:59:18, je pouvais donc affirmer :
G(Pi(1014))=693
Le record d'Andrew Odlyzko datant de 1993 était battu !
Simon Plouffe [14] annonçait le mardi 07/10/2025 à 02:25 pm (East Time) avoir montré,
lui aussi, que G(Pi(1014))=693,
plus de 24 heures après moi...
Il est très important de noter que Simon Plouffe et moi-même n'avons utilisé ni les mêmes méthodes, ni les mêmes programmes [15].
Le fait que nous trouvions tous les deux et indépendamment le même résultat garantit l'exactitude de la valeur 693.
Voici quelques informations relatives à la répartition des calculs sur les serveurs lors du calcul du premier record :
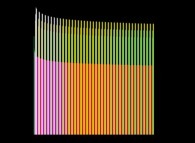
Le calcul continue actuellement au-delà de 1x1014 et se situe à partir du 10/11/2025 dans [3x1014,10x1014].
De nouveaux records apparaissent au fur et à mesure :
6-Les records absolus successifs [01] :
G(Pi(x)) = G(Pi(1014))=693 x ∈ [19563862928347,19595015607259] -05/10/2025, 20:59:18-
G(Pi(x)) = G(Pi(1.1000x1014))=701 x ∈ [108623442367669,108652648007513] -24/10/2025, 16:45:28-
G(Pi(x)) = G(Pi(1.1450x1014))=744 x ∈ [144875389408103,144906542089667] -27/10/2025, 12:10:26-
G(Pi(x)) = G(Pi(2.2000x1014))=773 x ∈ [218200934579443,218228193179959] -03/11/2025, 01:39:05-
G(Pi(x)) = G(Pi(2.8000x1014))=788 x ∈ [277889408099683,277908878538719] -08/11/2025, 17:46:01-
G(Pi(x)) = G(Pi(6.1500x1014))=800 x ∈ [613228193146423,613255451754013] -13/12/2025, 17:24:56-
G(Pi(x)) = G(Pi(1015))=800 x ∈ [613228193146423,613255451754013] -23/01/2026, 18:41:08-
G(Pi(x)) = G(Pi(1.0025x1015))=806 x ∈ [1002157201513887,1002157320872243] -24/01/2026, 00:51:08-
G(Pi(x)) = G(Pi(1.2075x1015))=809 x ∈ [1206596573208751,1206627725898989] -15/02/2026, 02:58:42-
G(Pi(x)) = G(Pi(1.2125x1015))=811 x ∈ [1212869937694721,1212889408142341] -15/02/2026, 21:50:58-
À la date du 18/03/2026,
15x4x10x96
= 57600
valeurs de G(Pi(x)) ont déjà été obtenues.
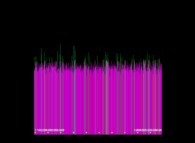
Les voici présentées en les regroupant par paquets de
8x96
= 768
et en en faisant la moyenne :
N=1 Moyenne768(G)=470 |----------------------------------------------*
N=2 Moyenne768(G)=494 |------------------------------------------------*
N=3 Moyenne768(G)=503 |-------------------------------------------------*
N=4 Moyenne768(G)=509 |-------------------------------------------------*
N=5 Moyenne768(G)=516 |--------------------------------------------------*
N=6 Moyenne768(G)=514 |--------------------------------------------------*
N=7 Moyenne768(G)=516 |--------------------------------------------------*
N=8 Moyenne768(G)=520 |---------------------------------------------------*
N=9 Moyenne768(G)=522 |---------------------------------------------------*
N=10 Moyenne768(G)=523 |---------------------------------------------------*
N=11 Moyenne768(G)=528 |---------------------------------------------------*
N=12 Moyenne768(G)=529 |---------------------------------------------------*
N=13 Moyenne768(G)=527 |---------------------------------------------------*
N=14 Moyenne768(G)=528 |---------------------------------------------------*
N=15 Moyenne768(G)=529 |---------------------------------------------------*
N=16 Moyenne768(G)=532 |----------------------------------------------------*
N=17 Moyenne768(G)=530 |----------------------------------------------------*
N=18 Moyenne768(G)=532 |----------------------------------------------------*
N=19 Moyenne768(G)=534 |----------------------------------------------------*
N=20 Moyenne768(G)=534 |----------------------------------------------------*
N=21 Moyenne768(G)=534 |----------------------------------------------------*
N=22 Moyenne768(G)=540 |-----------------------------------------------------*
N=23 Moyenne768(G)=537 |----------------------------------------------------*
N=24 Moyenne768(G)=538 |----------------------------------------------------*
N=25 Moyenne768(G)=537 |----------------------------------------------------*
N=26 Moyenne768(G)=538 |----------------------------------------------------*
N=27 Moyenne768(G)=537 |----------------------------------------------------*
N=28 Moyenne768(G)=539 |----------------------------------------------------*
N=29 Moyenne768(G)=541 |-----------------------------------------------------*
N=30 Moyenne768(G)=541 |-----------------------------------------------------*
N=31 Moyenne768(G)=543 |-----------------------------------------------------*
N=32 Moyenne768(G)=543 |-----------------------------------------------------*
N=33 Moyenne768(G)=542 |-----------------------------------------------------*
N=34 Moyenne768(G)=543 |-----------------------------------------------------*
N=35 Moyenne768(G)=541 |-----------------------------------------------------*
N=36 Moyenne768(G)=544 |-----------------------------------------------------*
N=37 Moyenne768(G)=543 |-----------------------------------------------------*
N=38 Moyenne768(G)=548 |-----------------------------------------------------*
N=39 Moyenne768(G)=544 |-----------------------------------------------------*
N=40 Moyenne768(G)=547 |-----------------------------------------------------*
N=41 Moyenne768(G)=546 |-----------------------------------------------------*
N=42 Moyenne768(G)=548 |-----------------------------------------------------*
N=43 Moyenne768(G)=546 |-----------------------------------------------------*
N=44 Moyenne768(G)=548 |-----------------------------------------------------*
N=45 Moyenne768(G)=548 |-----------------------------------------------------*
N=46 Moyenne768(G)=549 |-----------------------------------------------------*
N=47 Moyenne768(G)=547 |-----------------------------------------------------*
N=48 Moyenne768(G)=549 |-----------------------------------------------------*
N=49 Moyenne768(G)=544 |-----------------------------------------------------*
N=50 Moyenne768(G)=548 |-----------------------------------------------------*
N=51 Moyenne768(G)=547 |-----------------------------------------------------*
N=52 Moyenne768(G)=548 |-----------------------------------------------------*
N=53 Moyenne768(G)=549 |-----------------------------------------------------*
N=54 Moyenne768(G)=550 |------------------------------------------------------*
N=55 Moyenne768(G)=552 |------------------------------------------------------*
N=56 Moyenne768(G)=554 |------------------------------------------------------*
N=57 Moyenne768(G)=551 |------------------------------------------------------*
N=58 Moyenne768(G)=552 |------------------------------------------------------*
N=59 Moyenne768(G)=551 |------------------------------------------------------*
N=60 Moyenne768(G)=551 |------------------------------------------------------*
N=61 Moyenne768(G)=552 |------------------------------------------------------*
N=62 Moyenne768(G)=553 |------------------------------------------------------*
N=63 Moyenne768(G)=550 |------------------------------------------------------*
N=64 Moyenne768(G)=553 |------------------------------------------------------*
N=65 Moyenne768(G)=554 |------------------------------------------------------*
N=66 Moyenne768(G)=555 |------------------------------------------------------*
N=67 Moyenne768(G)=554 |------------------------------------------------------*
N=68 Moyenne768(G)=553 |------------------------------------------------------*
N=69 Moyenne768(G)=555 |------------------------------------------------------*
N=70 Moyenne768(G)=553 |------------------------------------------------------*
N=71 Moyenne768(G)=554 |------------------------------------------------------*
N=72 Moyenne768(G)=556 |------------------------------------------------------*
N=73 Moyenne768(G)=557 |------------------------------------------------------*
N=74 Moyenne768(G)=554 |------------------------------------------------------*
N=75 Moyenne768(G)=552 |------------------------------------------------------*
Évidemment, la tendance est globalement à la croissance, mais très très lente...
Le calcul jusqu'à 1.5x1015 a été interrompu à cette date, alors qu'il aurait
pu continuer encore pendant des milliards de milliards d'années (et encore beaucoup plus après le passage de 64 à 128 bits...) !
Une petite remarque :
1015 (ou plus...) peut sembler une valeur énorme, mais il n'en est rien.
En effet,
tous les nombres entiers sont inimaginables, inaccessibles,...
sauf les premiers évidemment. Or il en est de même des nombres premiers,
puisque leur ensemble est infini. Ainsi, s'il existe un contre-exemple à la conjecture de Proth-Gilbreath,
la probabilité pour qu'il soit accessible est très certainement quasiment nulle.
Voici une mise à jour du tableau publié en 1993 par Andrew Odlyzko :
x : Pi(x) : G(Pi(x)) : Date :
1013 346065536839 635 Andrew Odlyzko (1993).
1014 3204941750857 693 Jean-François Colonna (05/10/2025), Simon Plouffe (07/10/2025).
1015 29844570423226 800 Jean-François Colonna (23/01/2026).
7-Les records relatifs successifs [01] :
G(Pi(x)) = 1347 x ∈ [5733241593241096731,5733241593241296731] -27/02/2026, 12:33:21-
G(Pi(x)) = 1559 x ∈ [20733746510561342863,20733746510561542863] -01/03/2026, 17:51:08-
G(Pi(x)) = 1935 x ∈ [6021312001028259683626468703,6021312001028259683626668637] -06/03/2026, 18:52:00-
8-Les écarts entre nombres premiers :
Simultanément les écarts entre nombres premiers ont été calculés et associés éventuellement aux records absolus ou relatifs obtenus [01] :
Nombres premiers : écarts entre nombres premiers : G(Pi(x)) :
[Calculs 64 bits]
2 1
3 2
7 4
23 6
89 8
113 14
523 18
887 20
1129 22
1327 34
9551 36
15683 44
19609 52
31397 72
155921 86
360653 96
370261 112
492113 114
1349533 118
1357201 132
2010733 148
4652353 154
17051707 180
20831323 210
47326693 220
122164747 222
189695659 234
191912783 248
387096133 250
436273009 282
1294268491 288
1453168141 292
2300942549 320
3842610773 336
4302407359 354
10726904659 382
20678048297 384
22367084959 394
25056082087 456
42652618343 464
127976334671 468
182226896239 474
241160624143 486
297501075799 490
303371455241 500
304599508537 514
416608695821 516
461690510011 532
614487453523 534
738832927927 540
1346294310749 582
1408695493609 588
1968188556461 602
2614941710599 652
7177162611713 674
13829048559701 716
19581334192423 766 693 (record absolu)
42842283925351 778
90874329411493 804
171231342420521 806
218209405436543 906 773 (record absolu)
1189459969825483 916
1686994940955803 [16] 924 729
1693182318746371 1132 969
43841547845541059 1184 1199
55350776431903243 1198 439
80873624627234849 1220 1073
203986478517455989 1224 969
218034721194214273 1248 907
305405826521087869 1272 1059
352521223451364323 1328 1245
401429925999153707 1356 1057
418032645936712127 1370 1113
804212830686677669 1442 1083
1425172824437699411 1476 1218
5733241593241196731 1488 1347 (record relatif)
6787988999657777797 1510 1096
[Calculs 128 bits]
15570628755536096243 1526 329
17678654157568189057 1530 1316
18361375334787046697 1550 1305
18470057946260698231 1552 1325
18571673432051830099 1572 1200
20733746510561442863 1676 1559 (record relatif)
68068810283234182907 1724 1515
88409025774659694609269 1628 1320
88409026124861029148819 1574 1375
90111023769130809399029 1580 1158
91008005685955879916401 1612 1322
92008005233975799174049 1584 1521
93310024192891977362587 1624 1136
153125481414651411510001 1588 1357
157169790357596057379929 1668 1327
227125476252860770095113 1604 1417
275125480759770276082019 1644 1503
348125468109010265299271 1602 1263
444888024000161880076721 1578 1179
461003025023148162667033 1650 1097
475135024904107611376237 1750 495
506169788449647021511111 1638 1237
507139024133574480779581 1590 1243
511125438041415299421601 1572 1346
519125479346441609466023 1596 1412
601559025236668271908379 1620 439
645600025854624019250411 1598 1295
654774025979872326628579 1570 1176
671442875163990116829497 1632 1194
708664733765282327176751 1710 1543
808129786082486355062717 1586 1323
817125469610972857731061 1692 1437
822125462857195122741779 1634 1281
829125472095488458309583 1626 1517
908600025159019423417933 1654 1413
929125470064749912335467 1600 1429
1409619025494896363461087 1680 1355
1689619025236598760976829 1610 1320
1863007027058448917031433 1726 1525
2417837025702997028843443 1636 1308
2668123000582492119464617 1656 1333
4417837025271189172082513 1608 1312
4591958808448499496305287 1780 1257
4601311025550610228138711 1690 1579
4771561025190978473357407 1582 1317
4871005025825741055913559 1694 1501
5013267025248268009777159 1672 1226
5111827025410880328372583 1606 1379
5701963804766267176483453 1594 1072
9242091025170776894993897 1766 1427
10148375028695776627340501 1640 965
10234026002878309225086799 1648 1370
10234026003107509182675341 1676 1173
10503126003077789930911879 1630 1369
17853322005951711516168487 1686 1411
20383026002229098626547639 1592 1387
30011026001827477703636173 1740 1497
37039655026170596199293657 1752 391
37039655026277896461956917 1746 1439
38283026000105876456447549 1658 1307
39753026000841430736202739 1660 1457
40503126001716558768993799 1662 1313
42461577000200688572056091 1728 1540
50011026000605167554818833 1614 1430
50011026000985432236994141 1576 1001
50011026001254085912788547 1642 1232
50148375026035070947338349 1678 1433
50234026000970339549409247 1666 1424
50503126001280209002157267 1616 1499
50754026000858414432532293 1734 1456
55723122040086608203258649 1698 1435
69361551050100334908440329 1702 989
72753026003121484051877369 1754 1369
73283026003973067104501339 1674 1469
79139658026044243740847151 1646 1389
80184269026465047227041177 1722 1575
83753026001934316187838497 1682 1375
84199650026160877110518461 1732 1402
84523126003293348705947939 1622 1581
86087256026428977676556479 1830 1470
86283026003161194576775057 1762 1301
88148378027905948598974153 1618 957
90523126001136840586142237 1652 1341
90523126002000439101137111 1776 1617
90523126002091526467218463 1744 998
90523126002117844475997013 1704 1479
91084263026046832262353511 1808 1615
91283026002272823778115587 1854 1580
94283026000460650817643547 1806 1291
96523126000774442796493001 1718 1055
110449654697555438112561319 1684 1379
124127829027210048144492593 1736 1160
161023337027912452750278023 1664 1445
161023337027994323152086013 1936 1642
161023337028310365631639753 1696 721
161023337028376633976274427 1774 1347
167021551028816331494487719 1814 1103
169206313035910497586224637 1716 1427
169206313037524085550011021 1760 1111
172233338035577973225937699 1708 931
172233338035661427996026473 1860 1551
183245698035574395968790427 1872 1010
183245698038521377016396923 1804 1330
185265722028138732845783509 1812 1541
191506729036081185032535079 1720 1140
191506729036347786101707879 1824 1373
191506729036672524811449829 1758 1671
191506729038361825489489313 1844 1197
197021551027975628706026789 1688 1562
198245298028246350476778643 1764 1365
198245298028294569694862807 1724 1574
211506729033894836038769081 1800 1559
227021551027737529987065469 1810 1485
253022127027824187693016727 1790 1581
261023337027413737623820943 1706 1273
302233338032699490171225683 1730 1501
313245698033230889150530529 1700 1428
314206313032559556437705819 1778 1598
333245298028562639400861353 1670 1213
361023337029228675738125911 1818 1053
361023337029651191344064387 1770 1185
363253313027185154998755239 1712 1527
414127829027107949907596749 1768 1311
508253313027343345210322131 1786 1422
512233338030056680994432863 1840 1027
517021551027178550547527491 1798 1573
531506722030087317322633423 1756 1626
531506722032495269637700891 1870 1353
531506722032894991035261461 1788 1599
612233338029038274818850137 1866 1587
612233338029577635338157403 1834 1536
622337118707239085237867807 1850 1146
644853313030609631743421827 1792 1563
663853313028090003058817561 1796 1585
685245298027055418345996361 1990 1531
931506729027818356495510979 1772 290
931506729027974407041540707 1782 1281
1985698761742223986651814371 1738 1129
2518970080811424228048297851 1848 1721
2681804411030756891181329527 1816 1682
2681804411030796838102390267 1794 1591
2844230000030892453360363713 1920 1390
3001549619028368687092343141 1842 1384
3001549619029361061238343309 1934 1636
3039248000030181434897238311 1916 1839
3044230000030128405583745033 1944 1809
3281312000028041064344397077 1742 1195
3521777371029774497617670861 1902 1606
3681804411029893987474470217 1714 1427
3717737905029238085958241901 1748 1429
3733289118707267491829280101 1890 1589
3883778117029429378726839157 1852 1625
3883778117029553360606784223 1914 1661
4101238311033979111838291509 1858 880
4392804445028608016009081833 1918 1417
4521777371028573501293031019 1954 1669
4521777371028957272039263763 1886 1777
4603737621033901941540708091 1822 1628
4611238371029716324077383681 1922 1623
4883778117028144439778057967 1900 1433
5020547613028019048897910089 1784 1587
5570675040016229618538921497 1976 1465
5603737621032667844132289397 1894 1391
5739248000028792850873302491 1820 1289
5844230000028765302725127593 1884 1129
5851230000021967795781669357 1856 1186
5972248000023708695939463647 1826 1213
6021312001028259683626568699 1994 1935 (record relatif)
6101238311031688672705309009 1924 1401
6101239311029812830316130021 1802 559
6101239311030479007754228103 1946 1727
6139248000028643882072689133 1974 1372
6670605040015867559498340553 1960 1689
7051230000020674054592576303 1838 1343
7500230000000254312587886349 1832 1517
7500230000004410741095419811 1836 1317
7500230000005019060037933673 1888 1482
7500230000005824418875087691 1846 1600
7500230000011523034496281371 1982 1737
8012239000018115133439311463 1938 1769
8051230000019922137852468729 1980 1667
8101238311029153282478027583 1910 1749
8104778551030016778369544613 1868 1275
8511230000017373935165665319 1882 1621
8761007116028125697454115487 1892 1312
15251000000439240915164391943 1978 1597
15600350800200231835802693153 1898 1291
15600350800200591840837572687 1950 1777
16107428778765206909298916249 1948 1547
16107428778765313805063526049 1942 1435
16107428778766062769433544071 1862 1752
16817006514738017659250207459 1968 1595
16967428778771122673539497533 1908 1307
17361011751029174933335986203 1964 1580
17817006514740891827868262213 1896 1233
21119471029029007664840376149 1878 1743
21124471029101398728988856797 1926 1504
29045119029001077581773468231 1932 1412
29045119029001231341899676133 1828 1501
78965098027967495955787825381 1972 1240
83723413734029484073263062011 1962 1561
93010225055029330341377130337 1912 1252
93777234437032666433522975959 1930 1215
93777234437033872048058808383 1928 1216
93825139554000834758506871159 1880 901
94381705258295181151295669737 1876 1827
98731233432030301788380501897 1874 1345
484458149616032368701456021079 1864 1467
631337750259693153112235938121 1958 1656
801451149611030245636120895591 1992 1613
801451149611030624254364873641 1966 1467
892340838549031853833349514503 1940 1620
917123687913032561163805565423 1988 1275
927619616117030224870646906207 1904 1365
1611281318552031378980232272063 1998 1543
2304607319542032497749866213061 1956 1633
3809205709418032358337519745171 1986 1848
5887250233904031284472398660693 1970 1429
20282409603651671079340215344953 1984 1087
45154861419265032079255464330641 1952 1654
65013315500001000157495421077531 1906 1191
85982514713000000005643994785767 1996 1801
Copyright © Jean-François COLONNA, 2025-2026.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2025-2026.
