Proth-Gilbreath Conjecture
Beat the Andrew Odlyzko Record G(Pi(1013))=635 (1993)
G(Pi(1014))=693 on 10/05/2025 at 20:59:18
G(Pi(2.8000*1014))=788 on 11/08/2025 at 17:46:01
G(Pi(6.1500*1014))=800 on 12/13/2025 at 17:24:56
G(Pi(1015))=800 on 01/23/2026 at 18:41:08
G(Pi(1.0025*1015))=806 on 01/24/2026 at 00:51:08
G(Pi(1.2075*1015))=809 on 02/15/2026 at 02:58:42
G(Pi(1.2125*1015))=811 on 02/15/2026 at 21:50:58
CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[Real Numbers don't exist in Computers and Floating Point Computations aren't safe. [Les Nombres Réels n'existent pas dans les Ordinateurs et les Calculs Flottants ne sont pas sûrs.]]
[Please, visit A Virtual Machine for Exploring Space-Time and Beyond, the place where you can find more than 10.000 pictures and animations between Art and Science]
(CMAP28 WWW site: this page was created on 09/28/2025 and last updated on 02/19/2026 19:10:56 -CET-)
[en français/in french]
Preliminary Remark:
The following research is the fruit of a collaboration with Jean-Paul Delahaye professor at the Université de Lille,
researcher at the Lille Cristal laboratory and well known columnist for the Pour La Science newspaper.
Contents:
1-Introduction:
A conjecture
is a mathematical statement
that is believed to be true but cannot be called a theorem as long as every
attempt at a proof has failed...
The most beautiful recent example was Andrew Wiles's
proof of Fermat's Last Theorem in 1994, which had resisted the greatest mathematicians
since the 17th century.
Many important conjectures are currently "pending".
Such is the case for Goldbach's Conjecture -GC-
and the Twin Prime Conjecture -TPC-.
For a given conjecture, as long as no correct proof has been found, it is possible to try
to disprove it by finding a counterexample, when that makes sense. This is not the case for the
TPC, since no longer finding pairs of twin primes would in no way prove that, by searching
much further, new pairs would not appear. On the other hand, for GC, discovering
an even number greater than 2 that is not the sum of two primes would obviously prove that GC is false.
Unfortunately, if such a number exists, the likelihood of it being within our reach
is practically zero (in fact, all integers are enormous, indeed unimaginable, except,
of course, the small ones we use in everyday life...).
But even if the search for a counterexample
may sometimes seem futile, it can nevertheless be useful by revealing relevant information about
a given topic and this is the case for Gilbreath's Conjecture and prime numbers...
2-Definition:
This conjecture was stated in 1958 by Norman L. Gilbreath [01] but published earlier in 1878 by François Proth [02].
It is related to the prime numbers and to the sequences generated by taking the absolute value of
the difference between each prime number and its successor
and then repeating this process ad infinitum [03]:
2 3 5 7 11 13 17 19 23 29 31 (...)
\ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ /
1 2 2 4 2 4 2 4 6 2 (...)
\ / \ / \ / \ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ / \ / \ / \ /
1 0 2 2 2 2 2 2 4 (...)
\ / \ / \ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ / \ / \ /
1 2 0 0 0 0 0 2 (...)
\ / \ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ / \ /
1 2 0 0 0 0 2 (...)
\ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ / \ /
1 2 0 0 0 2 (...)
\ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ /
\ / \ / \ / \ / \ / \ /
1 2 0 0 2 (...)
\ / \ / \ / \ / \ /
\ / \ / \ / \ / \ /
\ / \ / \ / \ / \ /
\ / \ / \ / \ / \ /
1 2 0 2 (...)
\ / \ / \ / \ /
\ / \ / \ / \ /
\ / \ / \ / \ /
\ / \ / \ / \ /
1 2 2 (...)
\ / \ / \ /
\ / \ / \ /
\ / \ / \ /
\ / \ / \ /
1 0 (...)
\ / \ /
\ / \ /
\ / \ /
\ / \ /
1 (...)
\ /
\ /
\ /
\ /
(...)
The conjecture states that the first value of each line is 1 (except the first one where it is a 2 -the only even prime number-)
and was studied by Andrew Odlyzko in 1993. He did check it for all prime numbers less than 1013.
On sunday 10/05/2025 20:45 (Paris time, France) I did succeed to check it up to 1014
and on tuesday 10/07/2025 02:25 pm (East Time), Simon Plouffe (Canada) did the same.
Moreover he did confirm the maximal value (693) of the G(Pi(x)) [04] function with x ∈ [2,1014]
that was anticipated on 09/25/2025.
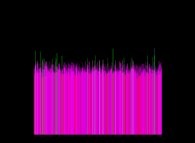
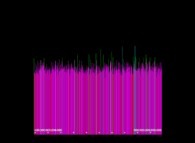
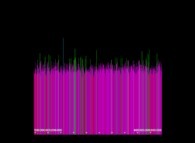
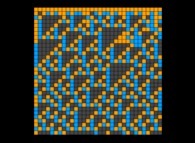
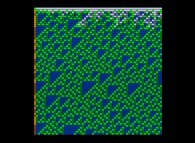
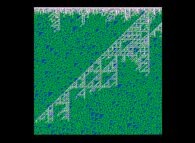
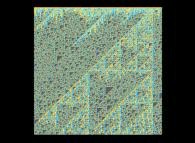
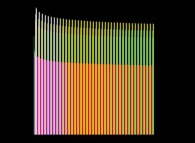
Here are some visualizations of this process
(first column (left): the difference signs, second column: the difference of the absolute values and third column: the differences):
x 
= 
x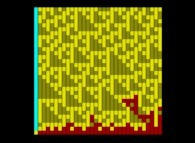 
= 
x 
= 
x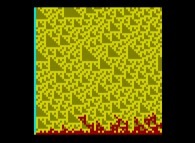 
= 
x 
= 
x 
= 
G(Pi(6.1500x1014))=800
x 
= 
G(Pi(1.0025x1015))=806
x 
= 
G(Pi(1.2075x1015))=809
x 
= 
G(Pi(1.2125x1015))=811
with the following colors regarding the numbers on the right pictures:
0 = Dark Cyan,
-1 = Dark Orange,
+1 = Light Orange,
-2 = Dark Green,
+2 = Light Green,
when all other numbers -{3,4,5,6,7,8,...}- are Grey (Dark and Light Grey respectively for the negative and positive numbers).
When the first used prime number is 2, according to the Proth-Gilbreath Conjecture, in the middle pictures, the left-hand side column must be Cyan ('1')
except the square at the very top that is Light Yellow ('2', the first prime number).
One can notice the yellow squares are defining monodimensional binary cellular automata.
3-The Theory:
Obviously one cannot check the Proth-Gilbreath Conjecture for there is an infinity of prime numbers.
Only a demonstration can solve this unless a counter-example is discovered, that is a line not starting with a '1'
(except the first one).
Let pn be the prime numbers:
p1=2
p2=3
p3=5
etc...
Let's define the suite dk(n):
d0(n) = pn for all n such as n > 0
dk(n) = |dk-1(n) - dk-1(n+1)| for all k such as k > 0 and for all n such as n > 0
Then one must check that:
dk(1) = 1 for all k such as k > 0
Due to the finite limits of computers, it is impossible to exhaustively check this property.
Fortunately Andrew Odlyzko noticed that if for a certain N there exists K such that:
dK(1) = 1
dK(n) ∈ {0,2} for all n such as 0 < n < N+1
then:
dk(1) = 1 for all k such as K-1 < k < N+K
Let's call G(N) the smallest k (if it exists) such that:
dj(1) = 1, 0 < j < k+1
dk(n) ∈ {0,2} for all n such as 0 < n < N+1
A trivial reasoning shows that G(N) does exist for all N and that the process can be stopped as soon as there are only '0's, '1's and '2's on the current line of rank k.
For example:
k=0 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71
≠ ≠ ≠ ≠≠ ≠≠ ≠≠ ≠≠ ≠≠ ≠≠ ≠≠ ≠≠ ≠≠ ≠≠ ≠≠ ≠≠ ≠≠ ≠≠ ≠≠ ≠≠
k=1 1 2 2 4 2 4 2 4 6 2 6 4 2 4 6 6 2 6 4
≠ ≠ ≠ ≠ ≠ ≠ ≠ ≠ ≠ ≠ ≠
k=2 1 0 2 2 2 2 2 2 4 4 2 2 2 2 0 4 4 2
≠ ≠ ≠ ≠
k=3 1 2 0 0 0 0 0 2 0 2 0 0 0 2 4 0 2
≠
k=4 1 2 0 0 0 0 2 2 2 2 0 0 2 2 4 2
≠
k=5 1 2 0 0 0 2 0 0 0 2 0 2 0 2 2
==> G=5
4-The Computation:
In 1993, Andrew Odlyzko verified this for all prime numbers less than 1013.
On Sunday, August 10, 2025, Jean-Paul Delahaye suggested to me "a fine calculation", nontrivial but seemingly feasible: the idea was to go beyond
1013 and reach, for example, 1014...
On paper, the task is simple: one merely has to follow the example above, but instead of stopping at 71, go past 1013.
It is clear that computers can neither store nor handle such a vast quantity of numbers. The idea, therefore, is to
work in successive blocks, each of a size compatible with the machines being used.
However, this subdivision cannot be done naïvely, as can be seen by cutting the previous example into two blocks:
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71
1 2 2 4 2 4 2 4 6 6 4 2 4 6 6 2 6 4
1 0 2 2 2 2 2 2 2 2 2 2 0 4 4 2
0 0 0 2 4 0 2
0 0 2 2 4 2
0 2 0 2 2
Obviously, the difference 31-29 is
missing. Jean-Paul Delahaye then suggested that the blocks should not be disjoint, but should
partially overlap as follows, based on an estimated G (taken as 5 below):
2 3 5 7 11 13 17 19 23 29 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71
1 2 2 4 2 4 2 4 6 4 2 4 6 2 6 4 2 4 6 6 2 6 4
1 0 2 2 2 2 2 2 2 2 2 4 4 2 2 2 2 0 4 4 2
1 2 0 0 0 0 0 0 0 2 0 2 0 0 0 2 4 0 2
1 2 0 0 0 0 0 2 2 2 2 0 0 2 2 4 2
1 2 0 0 0 2 0 0 0 2 0 2 0 2 2
that is:
2 3 5 7 11 13 17 19 23 29
13 17 19 23 29 31 37 41 43 47 53 59 61 67 71
== == == == ==
1 2 2 4 2 4 2 4 6
4 2 4 6 2 6 4 2 4 6 6 2 6 4
= = = =
1 0 2 2 2 2 2 2
2 2 2 4 4 2 2 2 2 0 4 4 2
= = =
1 2 0 0 0 0 0
0 0 2 0 2 0 0 0 2 4 0 2
= =
1 2 0 0 0 0
0 2 2 2 2 0 0 2 2 4 2
=
1 2 0 0 0
2 0 0 0 2 0 2 0 2 2
One might note that this overlap of 5 numbers significantly increases
the number of computations. In fact, this is true in this example, where each block
contains only 10 numbers. But the calculations that will be carried out to break the 1993 record will
use much larger blocks (generally of size 107), and even if the overlap used is
larger (typically around 1000), the number of additional computations due to the overlaps remains
relatively very small.
As for the choice of overlap size, it was guided by the results published in 1993 by Andrew Odlyzko:
x Pi(x) G(Pi(x))
102 25 5
103 168 15
104 1229 35
105 9592 65
106 78498 95
107 664579 135
108 5761455 175
109 50847534 248
1010 455052511 329
1011 4118054813 417
1012 37607912018 481
1013 346065536839 635
where 'x' is the last integer tested (the last prime number being strictly less
than x), 'Pi(x)' is the number of prime numbers in [1,x],
and finally 'G(Pi(x))' gives us the minimum overlap size.
The Hardware:
Six computers are used [05]: on the one hand, five computing servers ("C") that perform the actual
calculations, and on the other hand, a PC called the "Supervisor"
("S") that manages the distribution of the various computations among the
servers. All these machines run under Linux and are connected to an NFS file server. The configurations
below indicate, in order, the maximal number of processors [06], the memory capacity
in GB [07], and finally a performance index [08]:
- C1: {40,263,1}
- C2: {12,198,1.3875}
- C3: {12,148,1.48375}
- C4: {16,131,1.52857}
- C5: {36,528,1.6411}
The programs:
A set of programs designed to run on Linux computers has been written:
- A base program P1 in C, which is executed in parallel on all the active processors of the computing servers and receives the following arguments:
- The first integer PNE to be tested (not necessarily prime).
- The last integer DNE to be tested (not necessarily prime).
- The number of blocks NB defining the division of the interval [PNE,DNE].
- The number of prime numbers NPP defining the overlap between blocks.
- Several additional arguments, mainly used to monitor the progress of the computation.
This program defines the key function NextPrime(n), which returns the first prime number strictly greater than n,
using deterministic Miller-Rabin primality tests.
A main loop generates the NB blocks of the interval [PNE, DNE], incorporating the overlaps as needed. Then, an internal
loop successively scans each of these NB blocks to compute the differences defining the process.
In principle, this loop is repeated NNP times, but in practice, an optimization
interrupts it as soon as only '0's, '1's, or '2's remain.
At a given time, all occurences of P1 on the different servers Ci will be executed
with the lowest priority [09], which, combined with the very low memory "consumption"
[07], minimizes the inconvenience caused to other potential users.
- A script P2 in C Shell, executed on S, which evenly distributes the computations to be performed one block per
processor and waits until all the blocks have been processed.
This corresponds to a static allocation of blocks to processors.
However, since not all blocks require the same computation time [10],
it is clear that a dynamic allocation would have been preferable. To achieve this, it would
have sufficed to create smaller but more numerous blocks and place them in a queue. Then, whenever
any processor became free, it would fetch the next block from the head of the queue, continuing until the queue was empty.
However, since there are several different computing servers, this queue would have had to be an NFS-shared file.
Unfortunately, even when an NFS server is
properly configured, exclusive access during critical file update phases is not 100% reliable.
Experiments confirmed this, forcing the implementation of static allocation
- A script P3 in C Shell, executed on S, which divides the full computation into sub-tasks submitted to P2,
each requiring about five hours of processing.
This allows the entire computation to be interrupted (either intentionally or due to hardware failures)
and resumed later, losing only a few hours of work without losing useful information.
P3 also allows the launch of the different P2s to be spread out over time: this is why,
for the 10/05/2025 record, the calculations only took place during week-ends and weekday nights.
5-The Results:
The first computations started on saturday 09/20/2025 at 11:14:28 and then were suspended a few days due to the unavailability of the computing servers.
The final computation was completed [11] on Sunday, 10/05/2025, at 20:59:18 p.m. (Paris time,
France), as I reported in an email to Jean-Paul Delahaye at 10:36:20 p.m., informing
him of the end of the final stage (which concerned the prime numbers from 75,000,000,000,000
to 100,000,000,000,000). This confirmed an email I had sent him earlier,
on 09/25/2025, at 7:17:47 a.m.:
Bonne nouvelle: G(Pi(2x1013))=693
which indicated that G(Pi(1014)) would be greater than or equal to 693.
Therefore, on 10/05/2025, at 20:59:18 p.m., I was able to state:
G(Pi(1014))=693
The record held by Andrew Odlyzko since 1993 had been broken!
Simon Plouffe [12] announced on tuesday 10/07/2025, at 02:25 p.m. (Eastern Time)
that he had also found G(Pi(1014))=693, more than 24 hours after me...
It is very important to note that Simon Plouffe and I did not use the same methods or the same programs [13].
The fact that we both obtained the same result independently guarantees the accuracy of the value 693.
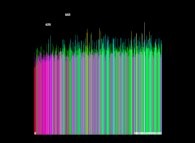
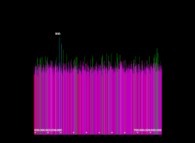
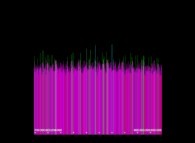
Here are some data regarding the processor usage during the first record computation:
The computation currently continues beyond 1x1014 and starting on 11/10/2025 is inside [3x1014,10x1014].
New records appear:
6-The Successive Records:
G(Pi(x)) = G(Pi(1014))=693 x ∈ [19563862928347,19595015607259] -10/05/2025, 20:59:18-
G(Pi(x)) = G(Pi(1.1000x1014))=701 x ∈ [108623442367669,108652648007513] -10/24/2025, 16:45:28-
G(Pi(x)) = G(Pi(1.1450x1014))=744 x ∈ [144875389408103,144906542089667] -10/27/2025, 12:10:26-
G(Pi(x)) = G(Pi(2.2000x1014))=773 x ∈ [218200934579443,218228193179959] -11/03/2025, 01:39:05-
G(Pi(x)) = G(Pi(2.8000x1014))=788 x ∈ [277889408099683,277908878538719] -11/08/2025, 17:46:01-
G(Pi(x)) = G(Pi(6.1500x1014))=800 x ∈ [613228193146423,613255451754013] -12/13/2025, 17:24:56-
G(Pi(x)) = G(Pi(1015))=800 x ∈ [613228193146423,613255451754013] -01/23/2026, 18:41:08-
G(Pi(x)) = G(Pi(1.0025x1015))=806 x ∈ [1002157201513887,1002157320872243] -01/24/2026, 00:51:08-
G(Pi(x)) = G(Pi(1.2075x1015))=809 x ∈ [1206596573208751,1206627725898989] -02/15/2026, 02:58:42-
G(Pi(x)) = G(Pi(1.2125x1015))=811 x ∈ [1212869937694721,1212889408142341] -02/15/2026, 21:50:58-
On 02/14/2026, 12x4x10x96 = 46080 values of G(Pi(x)) have already been obtained.
Here they are presented, grouped into sets of 8x96 = 768 and averaged:
N=1 Moyenne768(G)=470 |----------------------------------------------*
N=2 Moyenne768(G)=494 |------------------------------------------------*
N=3 Moyenne768(G)=503 |-------------------------------------------------*
N=4 Moyenne768(G)=509 |-------------------------------------------------*
N=5 Moyenne768(G)=516 |--------------------------------------------------*
N=6 Moyenne768(G)=514 |--------------------------------------------------*
N=7 Moyenne768(G)=516 |--------------------------------------------------*
N=8 Moyenne768(G)=520 |---------------------------------------------------*
N=9 Moyenne768(G)=522 |---------------------------------------------------*
N=10 Moyenne768(G)=523 |---------------------------------------------------*
N=11 Moyenne768(G)=528 |---------------------------------------------------*
N=12 Moyenne768(G)=529 |---------------------------------------------------*
N=13 Moyenne768(G)=527 |---------------------------------------------------*
N=14 Moyenne768(G)=528 |---------------------------------------------------*
N=15 Moyenne768(G)=529 |---------------------------------------------------*
N=16 Moyenne768(G)=532 |----------------------------------------------------*
N=17 Moyenne768(G)=530 |----------------------------------------------------*
N=18 Moyenne768(G)=532 |----------------------------------------------------*
N=19 Moyenne768(G)=534 |----------------------------------------------------*
N=20 Moyenne768(G)=534 |----------------------------------------------------*
N=21 Moyenne768(G)=534 |----------------------------------------------------*
N=22 Moyenne768(G)=540 |-----------------------------------------------------*
N=23 Moyenne768(G)=537 |----------------------------------------------------*
N=24 Moyenne768(G)=538 |----------------------------------------------------*
N=25 Moyenne768(G)=537 |----------------------------------------------------*
N=26 Moyenne768(G)=538 |----------------------------------------------------*
N=27 Moyenne768(G)=537 |----------------------------------------------------*
N=28 Moyenne768(G)=539 |----------------------------------------------------*
N=29 Moyenne768(G)=541 |-----------------------------------------------------*
N=30 Moyenne768(G)=541 |-----------------------------------------------------*
N=31 Moyenne768(G)=543 |-----------------------------------------------------*
N=32 Moyenne768(G)=543 |-----------------------------------------------------*
N=33 Moyenne768(G)=542 |-----------------------------------------------------*
N=34 Moyenne768(G)=543 |-----------------------------------------------------*
N=35 Moyenne768(G)=541 |-----------------------------------------------------*
N=36 Moyenne768(G)=544 |-----------------------------------------------------*
N=37 Moyenne768(G)=543 |-----------------------------------------------------*
N=38 Moyenne768(G)=548 |-----------------------------------------------------*
N=39 Moyenne768(G)=544 |-----------------------------------------------------*
N=40 Moyenne768(G)=547 |-----------------------------------------------------*
N=41 Moyenne768(G)=546 |-----------------------------------------------------*
N=42 Moyenne768(G)=548 |-----------------------------------------------------*
N=43 Moyenne768(G)=546 |-----------------------------------------------------*
N=44 Moyenne768(G)=548 |-----------------------------------------------------*
N=45 Moyenne768(G)=548 |-----------------------------------------------------*
N=46 Moyenne768(G)=549 |-----------------------------------------------------*
N=47 Moyenne768(G)=547 |-----------------------------------------------------*
N=48 Moyenne768(G)=549 |-----------------------------------------------------*
N=49 Moyenne768(G)=544 |-----------------------------------------------------*
N=50 Moyenne768(G)=548 |-----------------------------------------------------*
N=51 Moyenne768(G)=547 |-----------------------------------------------------*
N=52 Moyenne768(G)=548 |-----------------------------------------------------*
N=53 Moyenne768(G)=549 |-----------------------------------------------------*
N=54 Moyenne768(G)=550 |------------------------------------------------------*
N=55 Moyenne768(G)=552 |------------------------------------------------------*
N=56 Moyenne768(G)=554 |------------------------------------------------------*
N=57 Moyenne768(G)=551 |------------------------------------------------------*
N=58 Moyenne768(G)=552 |------------------------------------------------------*
N=59 Moyenne768(G)=551 |------------------------------------------------------*
N=60 Moyenne768(G)=551 |------------------------------------------------------*
Obviously, the overall trend is towards groth, but very very slowy...
At last, here is an update of the array published in 1993 by Andrew Odlyzko:
x Pi(x) G(Pi(x)) Date
1013 346065536839 635 Andrew Odlyzko (1993).
1014 3204941750857 693 Jean-François Colonna (10/05/2025), Simon Plouffe (10/07/2025).
1015 29844570423226 800 Jean-François Colonna (01/23/2026).
Finally, a small remark to conclude:
1015 may seem like an enormous value, but in fact it is not. Indeed,
all integers are unimaginable, inaccessible,...
except for the first ones, obviously. Yet the same is true of the prime numbers,
since their set is infinite. Thus, if there exists a counter example to the Proth-Gilbreath
conjecture, the probability that it is accessible is most certainly almost zero.
Copyright © Jean-François COLONNA, 2025-2026.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2025-2026.
