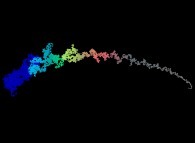
The special Liouville function displayed as a bidimensional random walk for the integer numbers from 2 to 100001 [La fonction spéciale de Liouville visualisée comme une marche aléatoire bidimensionnelle pour les nombres entiers de 2 à 100001].
The special Liouville function displayed as a bidimensional random walk for the integer numbers from 2 to 100001 [La fonction spéciale de Liouville visualisée comme une marche aléatoire bidimensionnelle pour les nombres entiers de 2 à 100001].
DPD(2) = 1
DPD(3) = 1
DPD(4) = 1
DPD(5) = 1
DPD(6) = 2
DPD(7) = 1
DPD(8) = 1
DPD(9) = 1
(...)
Let's recall that 1 is not a prime number when 2 is the first one (and the only even one...).
DPD(n)
sL(n) = (-1)
Hence:
sL(2) = -1
sL(3) = -1
sL(4) = -1
sL(5) = -1
sL(6) = +1
sL(7) = -1
sL(8) = -1
sL(9) = -1
(...)
X(0) = 0
Y(0) = 0
X(i+1) = X(i) + L(2*i+2)
Y(i+1) = Y(i) + L(2*i+3)
(the point {X(0),Y(0)} is on the right of the picture -white point-, when the colors used {magenta,red,yellow,green,cyan} are an increasing function of 'i')
with the one of the Liouville function 
.
and another superposition of three different computations: the integer numbers from 2 to 400001 (Red), 2 to 800001 (Green) and 2 to 1600001 (Blue) 
.