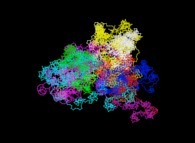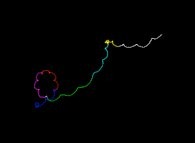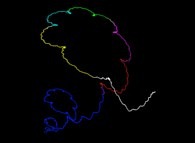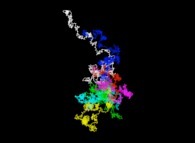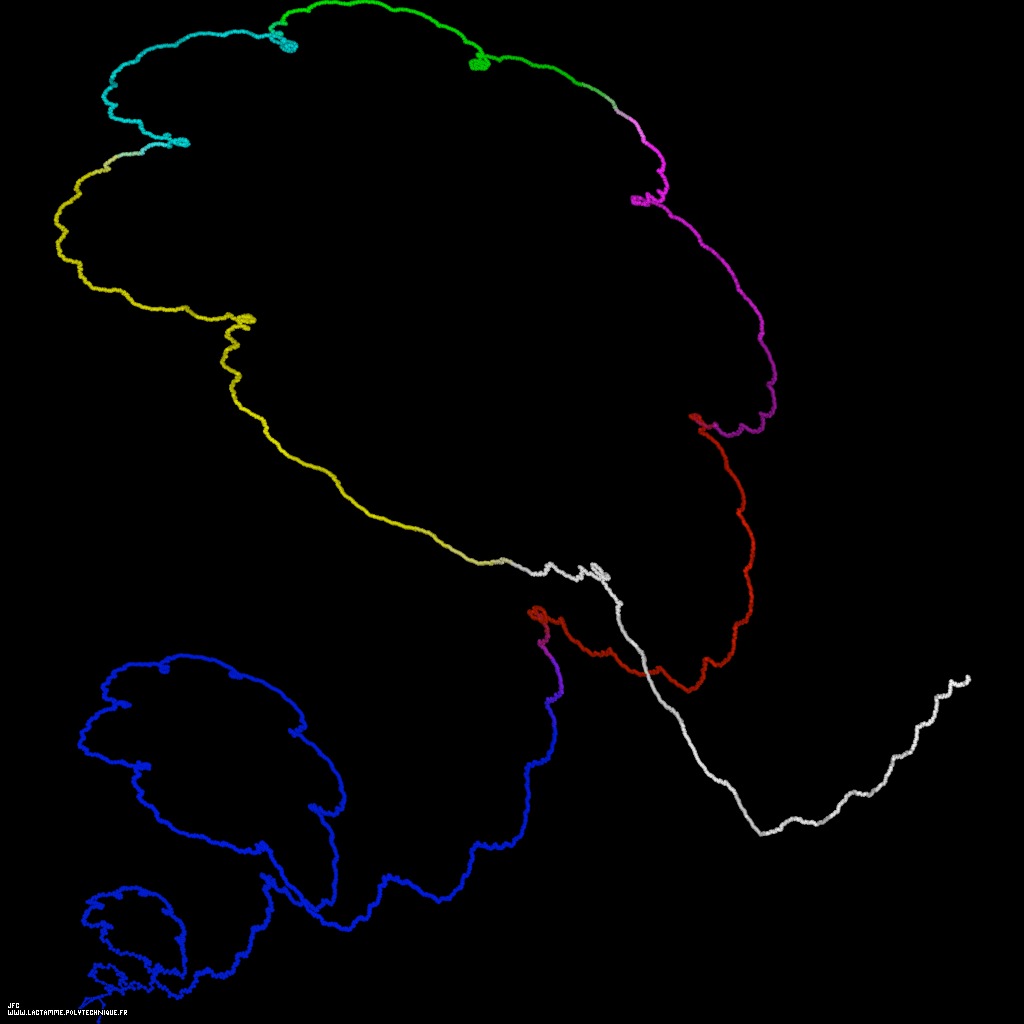
A bidimensional pseudo-random walk defined by means of the Champernowne number -using all base 10 prime numbers-: 0.2 3 5 7 11 13 17 19 23 29 31... -288.982 digits, base 10- [Une pseudo-marche aléatoire bidimensionnelle définie à l'aide du nombre de Champernowne -utilisant tous les nombres premiers en base 10-: 0.2 3 5 7 11 13 17 19 23 29 31... -288.982, base 10-].




Each digit N -base 10- defines the current step of an "absolute" bidimensional random walk using polar coordinates: 
                    RHO   = constant
                    THETA = 2.pi.N/10
'THETA' being an absolute angle. At last, the square root of the distance from each point to the origin is taken.


See some related pictures (possibly including this one):

 
 



(CMAP28 WWW site: this page was created on 12/26/2013 and last updated on 09/05/2024 08:57:37 -CEST-)



[See the generator of this picture [Voir le générateur de cette image]]

[See all related pictures (including this one) [Voir toutes les images associées (incluant celle-ci)]]

[Please visit the related NumberTheory picture gallery [Visitez la galerie d'images NumberTheory associée]]

[Go back to AVirtualMachineForExploringSpaceTimeAndBeyond [Retour à AVirtualMachineForExploringSpaceTimeAndBeyond]]

[The Y2K Bug [Le bug de l'an 2000]]

[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[Mail [Courrier]]
[About Pictures and Animations [A Propos des Images et des Animations]]


Copyright © Jean-François COLONNA, 2013-2024.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2013-2024.