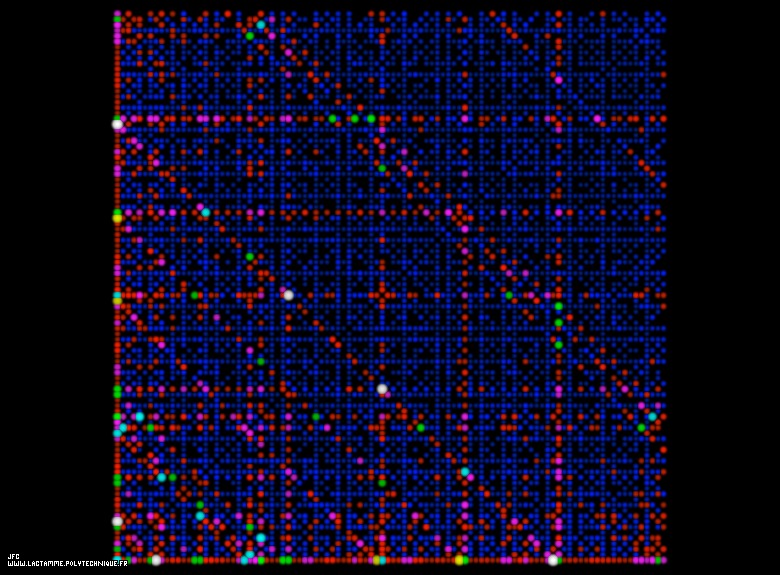
The ABC conjecture [La conjecture ABC].




The horizontal and vertical axes display respectively the integer numbers from 1 to N. Each disk display a couple of coprime numbers A (X axis) and B (Y axis): 
                    GCD(A,B)=1
The number C is the sum of A and B: 
                    C = A+B
The function Radical(N) gives the product of the prime factors (with an exponent equals to 1) of N. For example: 
                    N = 1960 = 23x51x72

                    Radical(1960) = 21x51x71 = 2x5x7 = 70


Then the following function is computed: 
                                      log(C)
                    k(A,B,C) = ---------------------
                                log(Radical(A.B.C))
The ABC conjecture states that k(A,B,C) is less than a certain constant (unknown, but greater than 1 and hopefully lesser than 2...) whatever the values of A and B.



The surface and the luminance of each disk are proportional to k(A,B,C).

For this picture, the numbers A and B belong to [1,N=100] giving birth to the following values: 
                    min(k(A,B,C))=0.37117806024788
                    max(k(A,B,C))=1.22629438553090



See some related pictures (including this one):




(CMAP28 WWW site: this page was created on 09/21/2012 and last updated on 09/06/2022 10:57:51 -CEST-)



[See all related pictures (including this one) [Voir toutes les images associées (incluant celle-ci)]]

[Please visit the related NumberTheory picture gallery [Visitez la galerie d'images NumberTheory associée]]

[Go back to AVirtualMachineForExploringSpaceTimeAndBeyond [Retour à AVirtualMachineForExploringSpaceTimeAndBeyond]]

[The Y2K Bug [Le bug de l'an 2000]]

[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[Mail [Courrier]]
[About Pictures and Animations [A Propos des Images et des Animations]]


Copyright © Jean-François Colonna, 2012-2022.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / Ecole Polytechnique, 2012-2022.