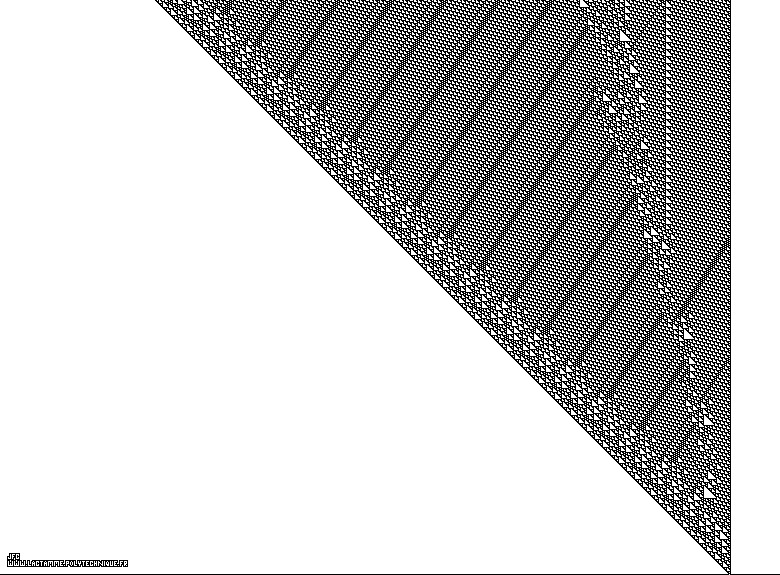
An elementary monodimensional binary cellular automaton -110- with 1 white starting point -bottom right- [Un automate cellulaire binaire monodimensionnel élémentaire -110- avec 1 point de départ blanc -en bas et à droite-].

An elementary monodimensional binary cellular automaton -110- with 1 white starting point -bottom right- [Un automate cellulaire binaire monodimensionnel élémentaire -110- avec 1 point de départ blanc -en bas et à droite-].
BBB = W
BBW = B
BWB = B
BWW = W
WBB = B
WBW = B
WWB = B
WWW = W
with, for example, "BWW = W" meaning:
if ((CELL(x-1,t)==Black)&&(CELL(x,t)==White)&&(CELL(x+1,t)==White)) then CELL(x,t+1)=WhiteThis cellular automaton is called 110. As a matter of fact, when concatenating the right-hand sides of the preceding rules one obtains:
-------- --------
WBBWBBBW = 10010001 = 01101110
and the binary number 01101110 equals the decimal number 110 (for 110=64+32+8+4+2).
It can be displayed as the following cubes:
WWB=B---------------WWW=W B-------------------W
/. /| /. /|
/ . / | / . / |
/ . / | / . / |
/ . / | / . / |
/ . / | / . / |
WBB=B---------------WBW=B | B-------------------B |
| . | | | . | |
| . | | | . | |
| . | | | . | |
| BWB=B...........|...BWW=W | B.............|.....W
| . | / | . | /
| . | / | . | /
^ | . | / | . | /
Y | Z | . | / | . | /
| / |. |/ |. |/
|/ BBB=W---------------BBW=B W-------------------B
O---->
X
the 'X', 'Y' and 'Z' axes being respectively the 'Right', 'Left' and 'Current' axes.
 and
and  ).
).