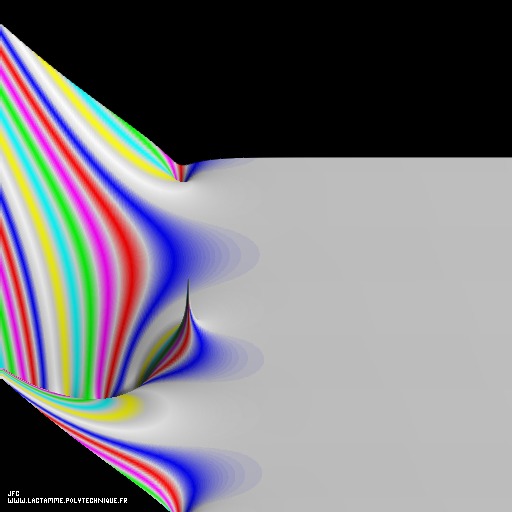
Tridimensional display of the Riemann Zeta function inside [-10.0,+20.0]x[-15.0,+15.0] [Visualisation tridimensionnelle de la fonction Zêta de Riemann dans [-10.0,+20.0]x[-15.0,+15.0]].

                            n=+infinity
                              _______
                              \
                               \       -s
                    Zeta(s) =  /      n
                              /______

                                n=1


                    \-/ s > 1

                            n=+infinity
                              _______
                              \
                               \       -z
                    Zeta(z) =  /      n
                              /______

                                n=1


                    \-/ z : Re(z) > 1

                              _________
                               |     |
                               |     |      1
                    Zeta(z) =  |     |  ---------
                               |     |        -z
                               |     |   1 - p

                                p E P

                               n=N-1
                              _______
                              \
                               \       -z
                    Zeta(z) =  /      n
                              /______

                                n=1

                                1-z      -z
                               N        N
                            + ------ + -----
                               z-1       2

                                k=V                        p=2k-2
                              _______                     ________
                              \          B                 |    |
                               \          2k    -z-(2k)+1  |    |
                            +  /      [-------.N           |    | (z+p)]
                              /______   (2k)!              |    |

                                k=1                          p=0

                            + epsilon(z,N,V)


                    \-/ z : Re(z+2V+1) > 1

                    N ~ |z|

• the absolute value of the Real part of Zeta(z),
• the absolute value of the Imaginary part of Zeta(z),
• the Modulus of Zeta(z),
• the Phase of Zeta(z).