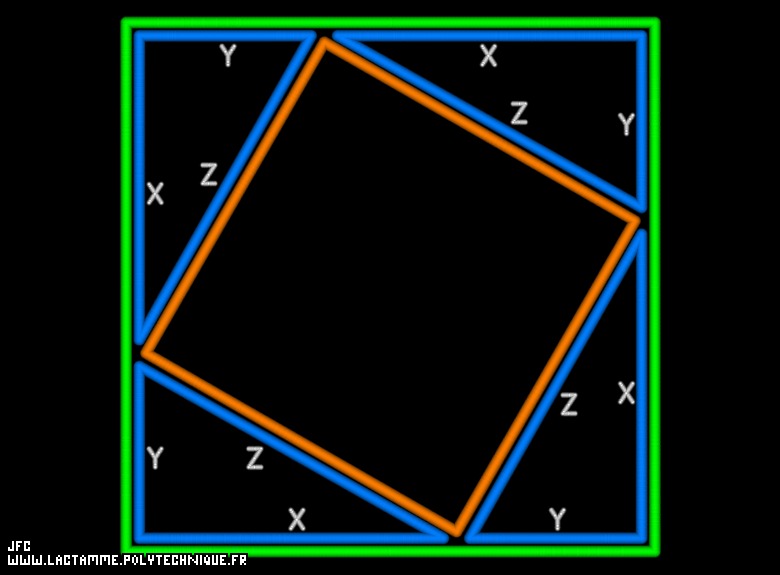
A demonstration of the Pythagoras' theorem [Une démonstration du théorème de Pythagore].

A demonstration of the Pythagoras' theorem [Une démonstration du théorème de Pythagore].
 ==>
==>  ==>
==>  ==>
==> 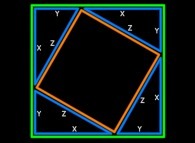
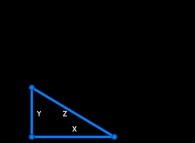
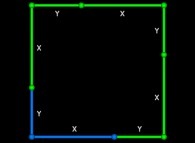
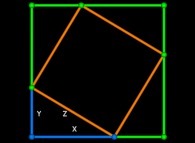
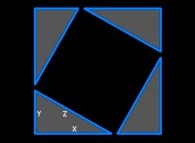
Surface(Green Square) = Surface(Red Square) + 4.Surface(Blue Triangle)
 =
=  +
+ 
2 2 1
(X+Y) = Z + 4.(---.X.Y)
2
___ ___
2 2 / \ 2 / \
X + Y + 2.X.Y = Z + 2.X.Y
\___/ \___/
2 2 2 X + Y = Z
CQFD