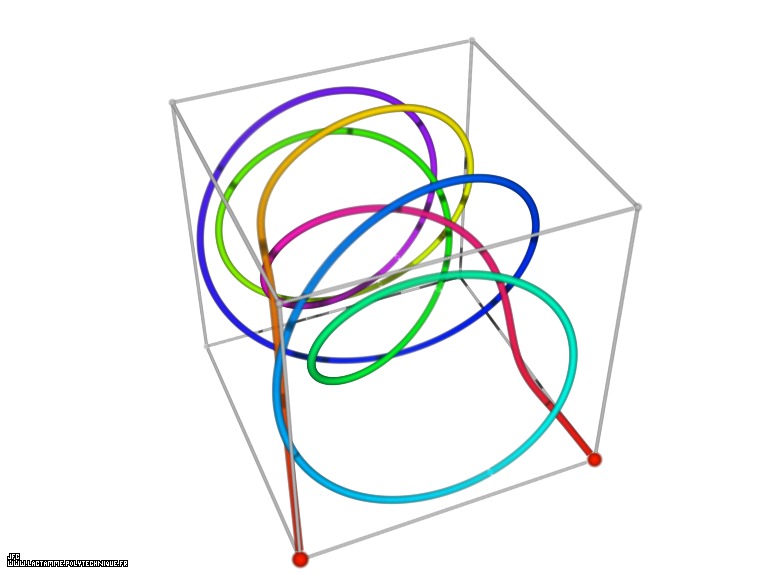
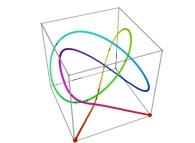
A Tridimensional Hilbert-like Curve defined with {X1(...),Y1(...),Z1(...)} and based on an 'open' 7-foil torus knot -iteration 1- [Une courbe tridimensionnelle du type Hilbert définie avec {X1(...),Y1(...),Z1(...)} et basé sur un nœud '7-trèfle' torique 'ouvert' -itération 1-].
The tridimensional Hilbert Curves:
Let's C1(T) being
a parametric curve  defined by means of 3 real functions of T
(T ∈ [0,1])
X1(T) ∈ [0,1], Y1(T) ∈ [0,1] and Z1(T) ∈ [0,1]
such as
:
defined by means of 3 real functions of T
(T ∈ [0,1])
X1(T) ∈ [0,1], Y1(T) ∈ [0,1] and Z1(T) ∈ [0,1]
such as
:
X1(T=0)=0 Y1(T=0)=0 Z1(T=0)=0 (lower left foreground corner)
X1(T=1)=1 Y1(T=1)=0 Z1(T=1)=0 (lower right foreground corner)
Then one defines a sequence of curves Ci(T) (i >= 1) as follows
:
Ci(T) = {Xi(T),Yi(T),Zi(T)} ∈ [0,1]x[0,1]x[0,1] --> Ci+1(T) = {Xi+1(T),Yi+1(T),Zi+1(T)} ∈ [0,1]x[0,1]x[0,1]
if T ∈ [0,1/8[:
Xi+1(T) = Xi(8T-0)
Yi+1(T) = Zi(8T-0)
Zi+1(T) = Yi(8T-0)
Transformation 1
if T ∈ [1/8,2/8[:
Xi+1(T) = Zi(8T-1)
Yi+1(T) = 1+Yi(8T-1)
Zi+1(T) = Xi(8T-1)
Transformation 2
if T ∈ [2/8,3/8[:
Xi+1(T) = 1+Xi(8T-2)
Yi+1(T) = 1+Yi(8T-2)
Zi+1(T) = Zi(8T-2)
Transformation 3
if T ∈ [3/8,4/8[:
Xi+1(T) = 1+Zi(8T-3)
Yi+1(T) = 1-Xi(8T-3)
Zi+1(T) = 1-Yi(8T-3)
Transformation 4
if T ∈ [4/8,5/8[:
Xi+1(T) = 2-Zi(8T-4)
Yi+1(T) = 1-Xi(8T-4)
Zi+1(T) = 1+Yi(8T-4)
Transformation 5
if T ∈ [5/8,6/8[:
Xi+1(T) = 1+Xi(8T-5)
Yi+1(T) = 1+Yi(8T-5)
Zi+1(T) = 1+Zi(8T-5)
Transformation 6
if T ∈ [6/8,7/8[:
Xi+1(T) = 1-Zi(8T-6)
Yi+1(T) = 1+Yi(8T-6)
Zi+1(T) = 2-Xi(8T-6)
Transformation 7
if T ∈ [7/8,1]:
Xi+1(T) = Xi(8T-7)
Yi+1(T) = 1-Zi(8T-7)
Zi+1(T) = 2-Yi(8T-7)
Transformation 8
Please note that 8=2d where d=3 is the space dimension.
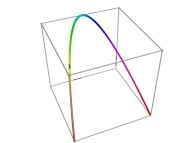
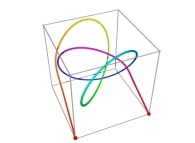
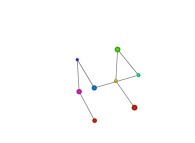
See a special C1(T) curve  in order to understand the geometrical meaning of the 8 transformations
in order to understand the geometrical meaning of the 8 transformations 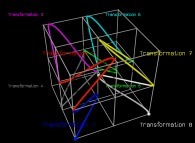 and of their order
and of their order  .
.
Here are the four first tridimensional Hilbert curves with an increasing number of iterations
:

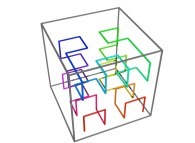
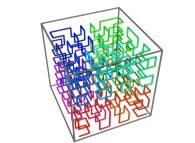
 [See the used color set to display the parameter T]
[See the used color set to display the parameter T]
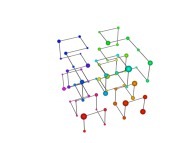
See the construction of one of them
:




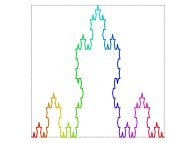
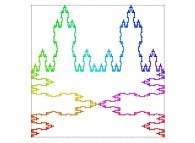
Here are some examples of Hilbert-like tridimensional curves using different generating curves and in
particular "open" knots
:
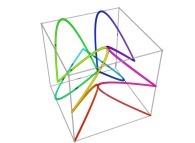
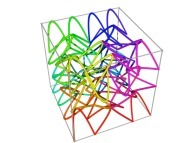

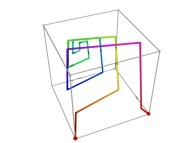
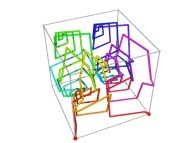

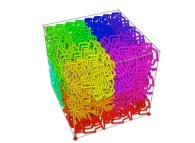
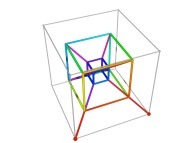
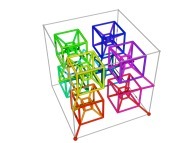
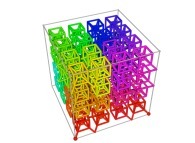




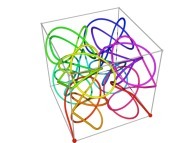


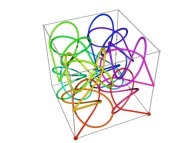
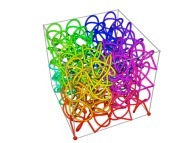





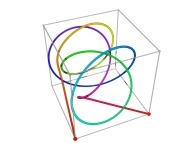
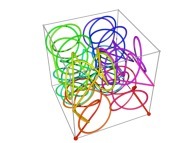



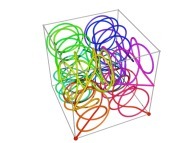

[More information about Peano Curves and Infinite Knots -in english/en anglais-]
[Plus d'informations à propos des Courbes de Peano et des Nœuds Infinis -en français/in french-]
The bidimensional Hilbert Curves:
Let's C1(T) being
a parametric curve 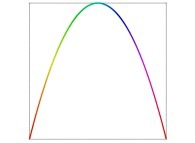 defined by means of 2 real functions of T
(T ∈ [0,1])
X1(T) ∈ [0,1] and Y1(T) ∈ [0,1]
such as
:
defined by means of 2 real functions of T
(T ∈ [0,1])
X1(T) ∈ [0,1] and Y1(T) ∈ [0,1]
such as
:
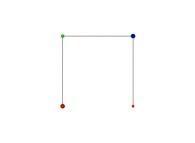
X1(T=0)=0 Y1(T=0)=0 (lower left corner)
X1(T=1)=1 Y1(T=1)=0 (lower right corner)
Then one defines a sequence of curves Ci(T) (i >= 1) as follows
:
Ci(T) = {Xi(T),Yi(T)} ∈ [0,1]x[0,1] --> Ci+1(T) = {Xi+1(T),Yi+1(T)} ∈ [0,1]x[0,1]
if T ∈ [0,1/4[:
Xi+1(T) = Yi(4T-0)
Yi+1(T) = Xi(4T-0)
Transformation 1
if T ∈ [1/4,2/4[:
Xi+1(T) = Xi(4T-1)
Yi+1(T) = 1+Yi(4T-1)
Transformation 2
if T ∈ [2/4,3/4[:
Xi+1(T) = 1+Xi(4T-2)
Yi+1(T) = 1+Yi(4T-2)
Transformation 3
if T ∈ [3/4,1]:
Xi+1(T) = 2-Yi(4T-3)
Yi+1(T) = 1-Xi(4T-3)
Transformation 4
Please note that 4=2d where d=2 is the space dimension.
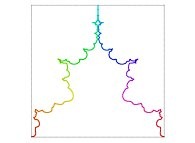
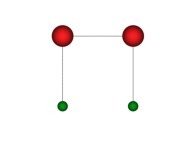
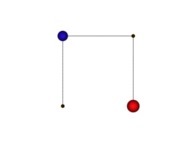
See a special C1(T) curve  in order to understand the geometrical meaning of the 4 transformations
in order to understand the geometrical meaning of the 4 transformations 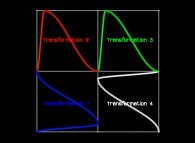 and of their order
and of their order  .
.
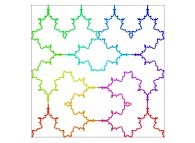
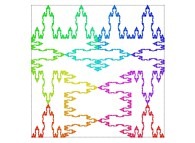
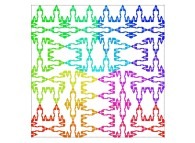
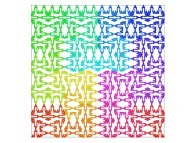
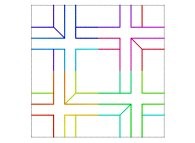
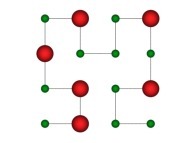
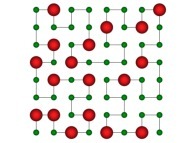
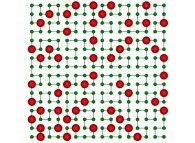
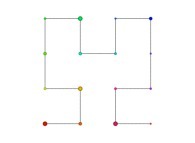
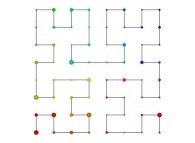
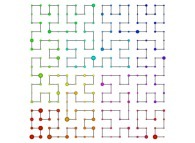
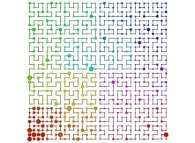
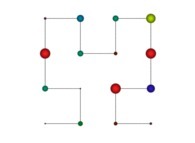
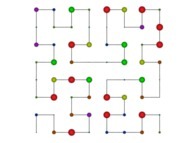
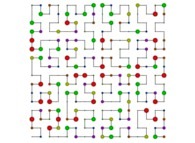
Here are the five first bidimensional Hilbert curves with an increasing number of iterations
:


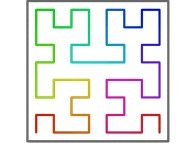

 [See the used color set to display the parameter T]
[See the used color set to display the parameter T]
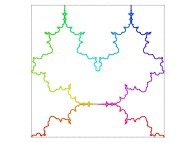
See the construction of some of them
:





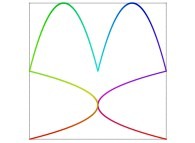
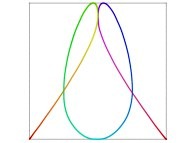
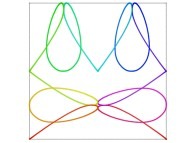
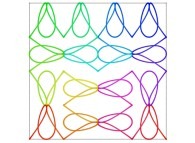
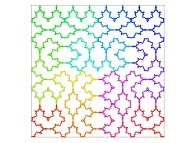
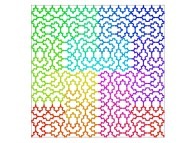
Here are some examples of Hilbert-like bidimensional curves using different generating curves
:




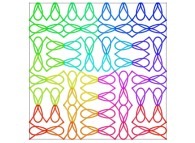







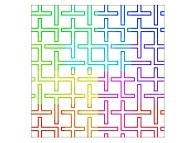
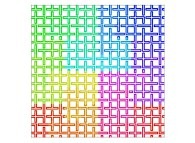

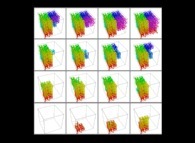
Here is the "mapping" of a few pictures by means of a bidimensional Hilbert curve:
:
width="TaBlE_WiDtH%"
 | ==>
[iteration 11] |  |
width="TaBlE_WiDtH%"
 | ==>
[iteration 10] |  |
width="TaBlE_WiDtH%"
 | ==>
[iteration 9] |  |
width="TaBlE_WiDtH%"
 | ==>
[iteration 10] |  |
See various Bidimensional Hilbert and Peano Curves (possibly including this one):


See Bidimensional Hilbert Curves, their nodes being "loaded" with some data (related to prime numbers, real number digits,...):

 See the used color set to display the parameter T.
See the used color set to display the parameter T.
 See the used color set to display the pi digits.
See the used color set to display the pi digits.




See various Tridimensional Hilbert and Peano Curves (possibly including this one):
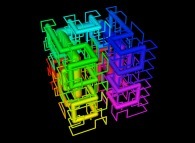
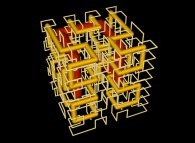
See Tridimensional Hilbert Curves, their nodes being "loaded" with some data (related to prime numbers, real number digits,...):
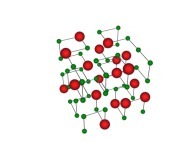
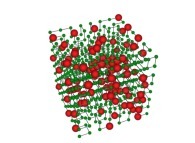




 See the used color set to display the parameter T.
See the used color set to display the parameter T.
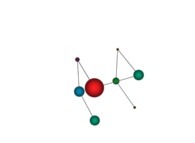
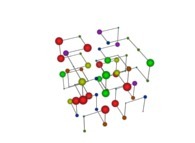
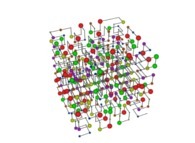

 See the used color set to display the pi digits.
See the used color set to display the pi digits.
(CMAP28 WWW site: this page was created on 05/17/2022 and last updated on 01/24/2025 18:15:47 -CET-)
[See the generator of this picture [Voir le générateur de cette image]]
[See all related pictures (including this one) [Voir toutes les images associées (incluant celle-ci)]]
[Please visit the related DeterministicFractalGeometry picture gallery [Visitez la galerie d'images DeterministicFractalGeometry associée]]
[Please visit the related NumberTheory picture gallery [Visitez la galerie d'images NumberTheory associée]]
[Go back to AVirtualMachineForExploringSpaceTimeAndBeyond [Retour à AVirtualMachineForExploringSpaceTimeAndBeyond]]
[The Y2K Bug [Le bug de l'an 2000]]
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[Mail [Courrier]]
[About Pictures and Animations [A Propos des Images et des Animations]]
Copyright © Jean-François COLONNA, 2022-2025.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2022-2025.

 defined by means of 3 real functions of T
(T ∈ [0,1])
X1(T) ∈ [0,1], Y1(T) ∈ [0,1] and Z1(T) ∈ [0,1]
such as
:
defined by means of 3 real functions of T
(T ∈ [0,1])
X1(T) ∈ [0,1], Y1(T) ∈ [0,1] and Z1(T) ∈ [0,1]
such as
:
 in order to understand the geometrical meaning of the 8 transformations
in order to understand the geometrical meaning of the 8 transformations  and of their order
and of their order  .
.


 [See the used color set to display the parameter T]
[See the used color set to display the parameter T]































 defined by means of 2 real functions of T
(T ∈ [0,1])
X1(T) ∈ [0,1] and Y1(T) ∈ [0,1]
such as
:
defined by means of 2 real functions of T
(T ∈ [0,1])
X1(T) ∈ [0,1] and Y1(T) ∈ [0,1]
such as
:
 in order to understand the geometrical meaning of the 4 transformations
in order to understand the geometrical meaning of the 4 transformations  and of their order
and of their order  .
.



 [See the used color set to display the parameter T]
[See the used color set to display the parameter T]


















































 See the used color set to display the parameter T.
See the used color set to display the parameter T.




 See the used color set to display the pi digits.
See the used color set to display the pi digits.

















