Brève Histoire Illustrée des Fractales
CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France
france telecom, France Telecom R&D
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[Real Numbers don't exist in Computers and Floating Point Computations aren't safe. [Les Nombres Réels n'existent pas dans les Ordinateurs et les Calculs Flottants ne sont pas sûrs.]]
[N'oubliez pas de visiter Une Machine Virtuelle à Explorer l'Espace-Temps et au-delà où vous trouverez plus de 10.000 images et animations à la frontière de l'Art et de la Science]
(Site WWW CMAP28 : cette page a été créée le 16/08/1999 et mise à jour le 03/10/2024 17:06:58 -CEST-)
(Texte présenté au Colloque Evolutions et Révolutions des Sciences et des Techniques au XXième et XXIième Siècles, Association Française pour l'Avancement des Sciences, Palais de la Découverte de Paris, 26/11/1999)
Résumé : Le concept mathématique de fractal est apparu récemment.
Il caractérise des objets possédant des détails à toutes les échelles d'observation, dont certaines
mesures peuvent diverger et dont la dimension
peut être non entière. De nombreux objets naturels possèdent
ces propriétés ; leur étude révèle alors qu'il peut être
fructueux de renoncer à l'hypothèse de différentiabilité
chère aux mathématiciens et aux physiciens.
Mots-Clefs :
Anaglyphes,
Art et Science,
Autostéréogrammes,
Chaos Déterministe,
Création Artistique,
Entrelacs,
Erreurs d'arrondi,
Expérimentation Virtuelle,
Génie Logiciel,
Géométrie Fractale,
Infographie,
Mathématiques,
Mécanique Céleste,
Mécanique Quantique,
Physique,
Sensibilité aux Erreurs d'Arrondi,
Simulation Numérique,
Stéréogrammes,
Synthèse de Phénomènes Naturels,
Synthèse de Texture,
Visualisation Scientifique,
Voyage Virtuel dans l'Espace-Temps.
1-Les Mathématiques, Reflet de notre Pensée et l'un des Langages de l'Univers :
Que sont nos Mathématiques ?
Même si les Mathématiques ne sont peut-être que
le reflet de nos structures cognitives les plus
profondes (Dieu ne fait certainement pas des Mathématiques),
elles se sont révélées, au cours des siècles,
être un langage puissant et suffisamment objectif pour décrire
l'Univers indépendamment de l'observateur, et nous permettre d'imaginer l'infini.
Ce serait faire preuve de peu d'humilité que de croire que
Nos Mathématiques sont le seul langage permettant cette
description. Cette adéquation notable vient certainement
de l'ordre qui règne dans l'Univers (si tout n'était que
chaos, il n'existerait aucune structure et donc
aucun observateur...) ; les symétries, les régularités
les invariants, les redondances,...
impliquent une possible "compression de l'information"
et donc l'existence de langages la décrivant.
Mais ainsi, que le déclarait Heinrich Hertz au
dix-neuvième siècle : on ne peut échapper au sentiment que
ces formules mathématiques ont une existence qui leur
est propre, qu'elles sont plus savantes que ceux qui les
ont découvertes, et que nous pouvons en extraire plus
de science qu'il n'en a été mis à l'origine. Ainsi, sans
vouloir offenser le génie d'Albert Einstein, il semble
évident que les trous noirs ou bien le Big Bang n'ont
pas été introduits volontairement dans les équations de
la Relativité Générale, et pourtant ils y sont présents,
et bien d'autres choses encore... Voici un exemple
plus proche de nous, celui des rétrogradations des
planètes du système solaire vues depuis Pluton,
obtenues tout simplement à partir des équations de
Newton 
.
2-De Euclide à Mandelbrot :
Encore récemment, malgré ces succès, des
"choses" bien quotidiennes échappaient encore aux
descriptions mathématiques : que sont en effet les
nuages, les montagnes, les arbres, les ramifications
des bronches,... en terme d'"atomes" euclidiens ?
Or à la fin du dix-neuvième siècle, des mathématiciens
(Weierstrass -peut-être le pionnier-, Cantor, Peano,
Lebesgue, Hausdorff, Besicovitch, von Koch,
Sierpinski,...) s'intéressèrent un temps à des
"monstres", et par exemple à des courbes continues
mais non différentiables, dont la longueur était infinie
bien que leur domaine soit limité ;
certaines réussissaient même à remplir fort bien des espaces de dimensions supérieures.
Charles Hermite y voyait là une plaie lamentable...
Ces courbes sont définies comme étant la limite à
l'infini d'un certain processus de construction itératif
et ne sont donc jamais visualisables exactement, mais
seulement de façon (très) approchée.
Voici l'exemple le plus simple à définir et à
appréhender : celui de la courbe de von Koch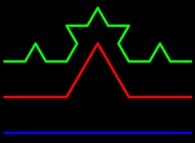 
. Nous
voyons ici les trois premières itérations de sa
construction : partant d'un segment (bleu en bas),
nous substituons au tiers central les deux côtés
supérieurs d'un triangle équilatéral ; cette procédure est
ensuite répétée pour chacun des segments plus petits
(dans un rapport égal à 3) obtenus. Il est évident qu'à
chaque itération la longueur totale est mutipliée par 4/3
(puique 3 petits segments ont été remplacés par 4 de
même taille), ce qui fait qu'en quatre-vingt dix itérations,
partant d'un segment d'un mètre, nous voici face à une
courbe dont la longueur est de l'ordre de la distance de
la Terre au Soleil ! Cela défie l'intuition, tout en mettant
en évidence une première propriété fondamentale :
un objet fractal permet au fini (dans le cas présent, le
domaine de définition de cette courbe) et a l'infini (sa longueur)
de coexister.
Une seconde propriété essentielle,
parfaitement visible ici, est celle d'autosimilarité. Elle
indique que les parties sont identiques au tout, à un
facteur d'échelle près : ainsi, le tiers gauche de la
courbe verte est une copie réduite (dans un rapport égal à 3)
de la courbe rouge entière.
Puis ces monstres restèrent assoupis quelques
dizaines années jusqu'à ce que la curiosité de certains,
et de Benoît Mandelbrot tout particulièrement (inventeur du
mot fractal et "père" de l'ensemble dit de Mandelbrot
), aidés par les progrès étonnants des
technologies informatiques, les réveillent. C'était, dans les années
soixante/soixante-dix, la [re-]naissance des
fractales.
3-L'Autosimilarité :
L'autosimilarité (néologisme issu de l'anglais self-similarity ;
autosimilitude aurait certainement été préférable comme traduction...)
semble être une propriété
possédée par de très nombreux objets naturels : un
nuage, une montagne,... Voici une branche de fougère 
:
la forme de l'un de ses détails est très proche de celle
de la branche entière.
Nous nous contenterons ici de cette propriété pour définir
un objet fractal, notant cependant qu'il peut être
défini d'une façon plus générale, comme possédant des structures
(alors non nécessairement identiques au facteur d'échelle près)
à toutes les échelles d'observation.
Cette propriété permet de comprendre que certaines de leurs mesures
puissent diverger (c'est le cas de la longueur de
la courbe de von Koch)
et que communiquer celles-ci sans indiquer simultanément
l'étalon utilisé, n'a pas de sens.
4-L'Universalité de la Géométrie Fractale :
La question se pose de savoir pourquoi tant
d'objets naturels sont fractals. L'examen d'un
exemple particulier, celui de la ramification des
bronches dans les poumons 
, peut nous fournir
la piste d'une réponse possible. En effet, cet
organe est destiné à assurer des échanges
gazeux à travers une surface dont l'aire doit être la
plus grande possible, alors que son
encombrement (et donc son volume) est limité.
Si la géométrie utilisée était, par exemple, celle
d'une sphère, pour augmenter l'aire il
conviendrait d'augmenter le rayon et donc
concomitamment le volume, ce qui serait
contraire à la contrainte imposée (notons, au
passage, que chez l'adulte la surface d'échange
est de l'ordre de 100 mètres carrés, ce qui
correspondrait à une sphère peu viable de 2.8
mètres de rayon !). Une structure fractale
semble être la réponse à ce problème
d'optimisation : les bronches ont ainsi une
surface énorme à l'intérieur du volume restreint
de la cage thoracique.
La Géométrie Fractale a
rapidement conquis ses galons d'outil mathématique
fondamental en réussissant à réunir alors des domaines
jusqu'alors disjoints. Les cours de la bourse et
le mouvement brownien 
,
le chaos déterministe 
,
les feux de forêts et les fronts de diffusion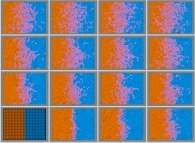 
,
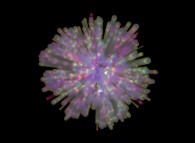
les agrégats 
, les
systèmes de pagination mémoire,... autant de
domaines de recherche où elle s'est imposée et d'où la "fractalité" émerge spontanément. Des
structures fractales sont ainsi repérées des plus petites
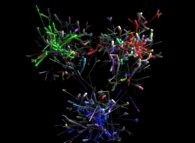aux plus grandes échelles
et certains vont même jusqu'à
attribuer à l'espace-temps une structure fractale, le
rendant ainsi continu et non différentiable.
Et la Science elle-même, avec les structures
sans fin qu'elle nous dévoile, ne serait-elle pas
l'ultime "objet" fractal ?
Par la suite, nous passerons sous silence la
délicate notion de dimension non entière. Notons
seulement qu'elle est fondamentale et en quelque sorte
une mesure de la "rugosité", de l'irrégularité,... des
objets fractals.
5-Géométrie Fractale et Synthèse de Phénomènes Naturels :
Examinons attentivement un exemple particulier :
celui de la synthèse de phénomènes naturels -paysages
et nuages-. Remarquons que la première itération de la
construction de la courbe de von Koch ressemble de
façon très shématique (et évidemment trop parfaite) à
la ligne de crête d'une montagne. En introduisant un
peu d'aléatoire, cette courbe pourra prendre une forme
moins régulière et donc plus naturelle ; cette courbe
sera alors qualifiée de fractale non déterministe.
L'auteur de ce texte
a généralisé cette procédure à des
espaces à N dimensions ; cela permet, par exemple,
pour N=3 de produire des paysages extrêmement variés
et pour N=4, de les animer 
.
Il convient de noter que la simplicité conceptuelle de cet algorithme
(et de ceux qui permettent de calculer les ensembles de Julia et de Mandelbrot, par exemple)
est pratiquement en opposition avec l'infinie richesse visuelle des structures obtenues.
Ainsi, la Géométrie Fractale est l'occasion de [re-]découvrir
que du simple peut naître le complexe...
6-Géométrie Fractale et Art :
La Géométrie Fractale est connue du public par les
images qu'elle permet donc de produire et qui font dire
bien souvent qu'elle est un pont entre l'Art et la
Science. S'il est vrai qu'elle a introduit des formes
nouvelles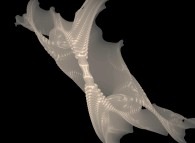 
, le créateur reste le maître et
l'initiateur de la composition 
.
Paraphrasant Heinrich Hertz déjà cité, il est possible
d'affirmer : on ne peut échapper au sentiment que
ces programmes ont une existence qui leur
est propre, qu'ils sont plus savants que ceux qui les
ont réalisés, et que nous pouvons en extraire plus
de science qu'il n'en a été mis à l'origine.
Alors, l'œuvre ne doit plus être vue dans le
résultat (une image par exemple), mais dans le
programme qui lui a donné naissance, introduisant
ainsi le concept "borgésien"
d'œuvre potentielle
(c'est-à-dire contenant en elle -et de façon presque utopique- une infinité
d'œuvres du même type, prêtes à émerger du néant)...
7-Ordinateur et Géométrie Fractale :
Le rôle joué par l'ordinateur semble avoir été
décisif dans ces progrès. Simultanément, il s'est
imposé dans toutes nos activités et bien évidemment
dans la recherche scientifique. Grâce a lui, une
approche expérimentale nouvelle, celle de
l'Expérimentation Virtuelle, associant l'étude
informatique du modèle mathématique d'un système
associé à la mise en images interactives des résultats
produits, a pu voir le jour au cours de ces dernières
années.
La Géométrie Fractale nous a montré que la
différentiabilité n'était pas nécessairement une
propriété naturelle et universelle ; y renoncer s'est
alors avéré une idée fructueuse ne demandant pas l'introduction
d'une hypothèse nouvelle en physique, bien au contraire...
Qu'en est-il aujourd'hui de la continuité ?
L'ordinateur, de par sa structure même, nous contraint
à y renoncer bien involontairement. Mais évidemment
il ne s'agit pas ici, du moins pas encore, de la
continuité supposée de la nature, mais bien de celle des
modèles ! Les nombres réels,
essentiels aux Mathématiques et à la Physique,
en particulier pour l'obtention d'équations différentielles via des passages
à la limite, sont impossibles à représenter dans nos
calculateurs, machines "discrètes" par définition.
Cette impossibilité peut conduire très facilement à
des résultats faux 
.
Les limites inhérentes de l'informatique doivent donc être connues et si possible
maitrisées, afin de tirer le meilleur parti des outils
fondamentaux qu'elle nous offre, pour aller toujours plus loin sur la voie de la Connaissance.
8-La révolution fractale :
La Géométrie Fractale est une géométrie des systèmes irréguliers et
qui permet donc d'unifier en quelque sorte les probabilités (le mouvement brownien 
),
les itérations et les interfaces 
.
C'est donc un langage commun.
A côté des symétries classiques de la Physique (invariance
par translation dans l'espace -conservation de la quantité de
mouvement-, invariance par translation dans le temps -conservation
de l'énergie- et invariance par rotation -conservation du moment
cinétique-), la Géométrie Fractale introduit une nouvelle symétrie :
celle de l'invariance d'échelle 
.
Une propriété fondamentale des objets fractals est celle de la
cohabitation de mesures à la fois finie et infinie que cette
géométrie permet (ce qu'illustre parfaitement notre système
respiratoire 
...). Et c'est certainement l'explication de son
omniprésence dans la nature. On pourrait donc, pour plaisanter,
compléter l'affirmation d'Albert Einstein "Dieu ne joue pas aux dés",
en ajoutant "mais il fait certainement de la Géométrie Fractale"...
Et maintenant, visitez les galeries d'images fractales
déterministes,
non déterministes
et artistiques.
Copyright © Jean-François COLONNA, 1999-2024.
Copyright © France Telecom R&D and CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 1999-2024.
