The Syracuse Conjecture for U(0)={1,2,3,4,...,256} -monodimensional display- [La conjecture de Syracuse pour U(0)={1,2,3,4,...,256} -visualisation monodimensionnelle-].

The Syracuse Conjecture for U(0)={1,2,3,4,...,256} -monodimensional display- [La conjecture de Syracuse pour U(0)={1,2,3,4,...,256} -visualisation monodimensionnelle-].
U = N (an integer number [un nombre entier]) > 0
0
if U is even [si U est pair] :
n n
U
n
U = ----
n+1 2
else [sinon] :
U = 3*U + 1
n+1 n
U(0) = 7
U(1) = 22
U(2) = 11
U(3) = 34
U(4) = 17
U(5) = 52
U(6) = 26
U(7) = 13
U(8) = 40
U(9) = 20
U(10) = 10
U(11) = 5
U(12) = 16
U(13) = 8
U(14) = 4
U(15) = 2
U(16) = 1
U(0) = 1 (0.00%) : {U(n)}={0001}
U(0) = 2 (50.00%) : {U(n)}={0001,0002}
U(0) = 3 (62.50%) : {U(n)}={0001,0002,0004,0008,0016,0005,0010,0003}
U(0) = 4 (66.67%) : {U(n)}={0001,0002,0004}
U(0) = 5 (66.67%) : {U(n)}={0001,0002,0004,0008,0016,0005}
U(0) = 6 (66.67%) : {U(n)}={0001,0002,0004,0008,0016,0005,0010,0003,0006}
U(0) = 7 (64.71%) : {U(n)}={0001,0002,0004,0008,0016,0005,0010,0020,0040,0013,0026,0052,0017,0034,0011,0022,0007}
U(0) = 8 (75.00%) : {U(n)}={0001,0002,0004,0008}
U(0) = 9 (65.00%) : {U(n)}={0001,0002,0004,0008,0016,0005,0010,0020,0040,0013,0026,0052,0017,0034,0011,0022,0007,0014,0028,0009}
U(0) = 10 (71.43%) : {U(n)}={0001,0002,0004,0008,0016,0005,0010}
0001 0002 0004 0008 0016 0005 0010 0020 0040 0013 0026 0052 0017 0034 0011 0022 0007 0014 0028 0009
0001 0002 0004 0008 0016 0005 0010 0020 0040 0013 0026 0052 0017 0034 0011 0022 0007
0001 0002 0004 0008 0016 0005 0010 0003 0006
0001 0002 0004 0008 0016 0005 0010 0003
0001 0002 0004 0008 0016 0005 0010
0001 0002 0004 0008 0016 0005
0001 0002 0004 0008
0001 0002 0004
0001 0002
0001
--> 0014 0028 0009
|
--> 0020 0040 0013 0026 0052 0017 0034 0011 0022 0007
|
| --> 0006
| |
|--> 0003
|
--> 0010
|
--> 0016 0005
|
--> 0008
|
--> 0004
|
--> 0002
|
0001
 of U(n).
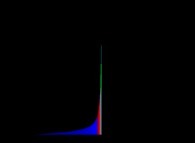
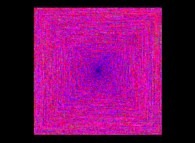
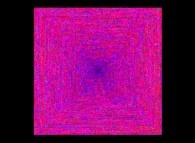
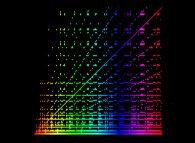
See the colors used (the smallest U(n) -equals to 1- is on the left-hand side when the biggest -equals to 13120- is on the right-hand side):
of U(n).
See the colors used (the smallest U(n) -equals to 1- is on the left-hand side when the biggest -equals to 13120- is on the right-hand side):