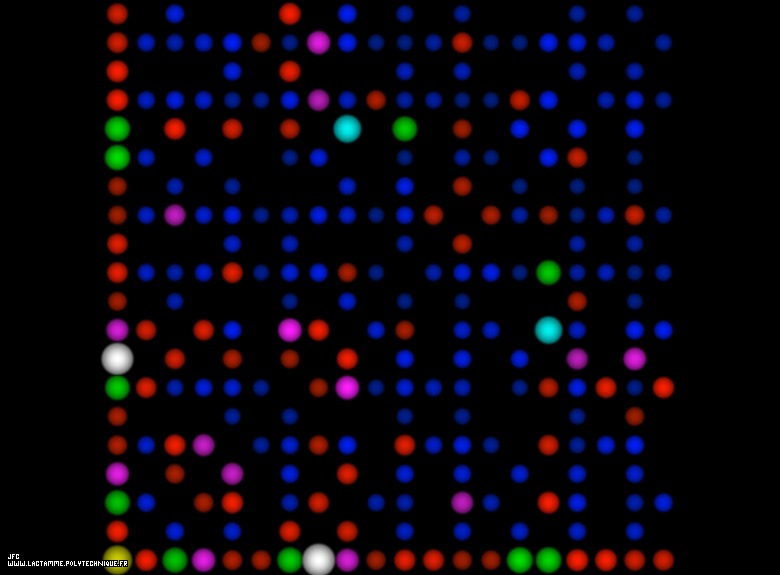
The ABC Conjecture [La conjecture ABC].
The horizontal and vertical axes display respectively the integer numbers from 1 to N.
Each disk display a couple of coprime numbers A (X axis) and B (Y axis):
GCD(A,B)=1
The number C is the sum of A and B:
C = A+B
The function Radical(N) gives the product of the prime factors (with an exponent equals to 1) of N.
For example:
N = 1960 = 23x51x72
Radical(1960) = 21x51x71 = 2x5x7 = 70
Then the following function is computed:
log(C)
k(A,B,C) = ---------------------
log(Radical(A.B.C))
The ABC conjecture states that k(A,B,C) is less than a certain constant (unknown, but greater than 1 and
hopefully lesser than 2...) whatever the values of A and B.
The surface and the luminance of each disk are proportional to k(A,B,C).
For this picture, the numbers A and B belong to [1,N=20]
giving birth to the following values:
min(k(A,B,C))=0.38418327328527
max(k(A,B,C))=1.22629438553090
See some tridimensional visualizations:

See some related pictures (including this one):



(CMAP28 WWW site: this page was created on 09/26/2012 and last updated on 02/16/2025 10:57:37 -CET-)
[See the generator of this picture [Voir le générateur de cette image]]
[See all related pictures (including this one) [Voir toutes les images associées (incluant celle-ci)]]
[Go back to AVirtualMachineForExploringSpaceTimeAndBeyond [Retour à AVirtualMachineForExploringSpaceTimeAndBeyond]]
[The Y2K Bug [Le bug de l'an 2000]]
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[Mail [Courrier]]
[About Pictures and Animations [A Propos des Images et des Animations]]
Copyright © Jean-François COLONNA, 2012-2025.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2012-2025.






