Visualisation de la Science
et
Science de la Visualisation






Jean-François COLONNA
[Contact me]

www.lactamme.polytechnique.fr

CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France
france telecom, France Telecom R&D

[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[Real Numbers don't exist in Computers and Floating Point Computations aren't safe. [Les Nombres Réels n'existent pas dans les Ordinateurs et les Calculs Flottants ne sont pas sûrs.]]
[N'oubliez pas de visiter Une Machine Virtuelle à Explorer l'Espace-Temps et au-delà où vous trouverez plus de 10.000 images et animations à la frontière de l'Art et de la Science]
(Site WWW CMAP28 : cette page a été créée le 26/10/1999 et mise à jour le 03/10/2024 17:20:14 -CEST-)



Mots-Clefs : Anaglyphes, Art et Science, Autostéréogrammes, Chaos Déterministe, Création Artistique, Entrelacs, Erreurs d'arrondi, Expérimentation Virtuelle, Génie Logiciel, Géométrie Fractale, Infographie, Mathématiques, Mécanique Céleste, Mécanique Quantique, Physique, Sensibilité aux Erreurs d'Arrondi, Simulation Numérique, Stéréogrammes, Synthèse de Phénomènes Naturels, Synthèse de Texture, Visualisation Scientifique, Voyage Virtuel dans l'Espace-Temps.



Au cours de ces dernières années, les métiers de l'image ont vécu, par l'introduction des techniques numériques [01], une série de bouleversements sans précédents. Si, par la production cinématographique à grand spectacle, cette révolution est bien connue du grand public, il en est une autre qui se fait simultanément et plus discrètement dans un domaine très différent, celui de la recherche scientifique et industrielle, mais dont les racines sont les mêmes : l'omniprésence de l'ordinateur. Nous allons montrer dans les lignes qui suivent que les chercheurs et les ingénieurs disposent aujourd'hui d'un nouvel outil permettant de porter plus loin leurs regards et leurs gestes.

Lever et coucher du Soleil ou encore chute inexorable des pommes : depuis la nuit des temps l'homme observe les régularités et les symétries de son univers. Pour les décrire, en particulier dans le domaine de la physique, c'est le langage des mathématiques qui est utilisé et aujourd'hui, toutes les grandes lois de la nature sont exprimées sous la forme d'équations qui n'ont bien souvent pas d'équivalents dans nos langues naturelles. Ces équations ne font pas qu'engranger ou transmettre des connaissances ; elles permettent aussi d'en produire de nouvelles [02]. Bien évidemment, ces prédictions n'ont de sens que si elles sont ensuite confrontées à l'expérience ; une théorie scientifique se devant d'être, par essence, réfutable.

Des modèles mathématiques [03] vont donc décrire le comportement des systèmes que les chercheurs et les ingénieurs étudient. Ainsi qu'il est facile de l'imaginer, ils sont en général d'une très grande complexité ; leur étude pourra donc présenter des difficultés tant théoriques que techniques, parfois insurmontables, dont l'encadré 1 donne un aperçu. Que faire ? Sommes-nous alors dans une impasse ? Heureusement, au cours des années quarante, John Von Neumann, et beaucoup d'autres, ont développé les premiers ordinateurs, grâce auxquels, aujourd'hui, nous sommes capables de calculer tout et parfois n'importe quoi, comme nous le verrons par la suite. Des méthodes dites numériques vont nous permettre de connaitre les solutions des équations, non point sous la forme générale de formules inexistantes ou inaccessibles, mais sous celle particulière de valeurs numériques. Cette situation ne doit d'ailleurs pas nous choquer. N'oublions pas que l'acte fondamental du scientifique est la mesure : la réalité ne se manifeste à lui, au cours des expériences, que par l'intermédiaire de nombres (des coordonnées, des vitesses, des températures,...) ; il n'a jamais accès aux formules du "Vieux" (pour paraphraser Albert Einstein...).

Que faire alors des résultats obtenus ? Dans la cas du problème des N-corps (revoir l'encadré 1), la situation n'est pas dramatique, puisque le nombre de valeurs obtenues n'excède pas quelques dizaines de milliers. Malgré cela, la contemplation de celles-ci ne révélerait pas aisément ce qui, en fait, saute immédiatement aux yeux lorsqu'elles sont mises en images d'une façon tout à fait naturelle (c'est-à-dire telle que les corps étudiés seraient perçus dans l'espace physique). En effet, la figure 1 montre instantanément et sans effort de réflexion, que les trajectoires ne sont pas des ellipses, et même, ne sont pas périodiques. Il est alors évident, que dans des situations fréquentes, ou le volume de résultats s'exprime en milliards (ou davantage encore), le recours à l'image de synthèse est incontournable. De plus, ainsi que cela fut rappelé précédemment, l'acte de mesure est fondamental ; les expériences qui sont actuellement menées, par exemple, avec les accélérateurs de particules ou les télescopes, donnent elles aussi des montagnes de résultats numériques. L'image de synthèse est donc tout aussi utile dans ce contexte. Il n'est certainement pas exagéré de dire qu'elle est aux expériences d'aujourd'hui ce que les aiguilles des appareils de mesures étaient aux expériences d'hier.

Avant d'en explorer plus avant les possibilités, il est bon de montrer dès à présent les difficultés et les dangers de ces techniques. Tout reposant sur l'ordinateur, la programmation sous-jacente conditionnera bien entendu la qualité, la valeur et la cohérence des résultats scientifiques obtenus. Mais une programmation exempte d'erreurs (sachant que, en dehors d'exemples simplistes, elle n'existe malheureusement pas...) est-elle garante de cette qualité ? Nous allons montrer qu'il n'en est rien. Trois raisons vont se conjuguer pour rendre parfois douteux nos résultats ; en effet, contrairement peut-être à certaines idées preconçues, il est difficile d'une part de calculer à l'aide d'un ordinateur, d'autre part de visualiser des résultats numériques et enfin de résister à la tentation de faire des images spectaculaires sans intérêt scientifique (ou pédagogique)...

Tout se ramène donc à des calculs réalisés à l'aide d'ordinateurs. La précision des opérations [04] est limitée pour des raisons théoriques, pratiques et économiques évidentes ; les machines font donc des erreurs d'arrondi [05]. En toute généralité, cela fait perdre à l'addition et surtout à la multiplication leur propriété d'associativité [06]. Pour des applications de type bureautique, cela n'a aucune conséquence perceptible ; par contre, dans le domaine scientifique, où les résultats sont transformés et retransformés un nombre de fois gigantesque, cela peut avoir, dans le cadre des modèles dits non linéaires, des implications dramatiques (voir la figure 2).

En ce qui concerne la visualisation, contrairement à la synthèse d'image spectaculaire évoquée en introduction, il s'agit ici de montrer bien souvent des objets sans image, soit qu'ils n'existent pas dans la nature (voir la figure 3), soit que, bien que naturels, il soit impossible, voire interdit, de les représenter (voir la figure 4) ou encore tout simplement parce qu'ils n'ont pas d'équivalents visuels (une pression ou une température par exemple...). S'il est clair que montrer un objet à quatre dimensions est chose difficile (revoir la figure 3), il est malheureusement moins évident que toute tentative de représentation, dans ce domaine, est délicate. La difficulté vient bien entendu des espaces, en général non naturels, dans lesquels résident ces objets, mais surtout de la non unicité des images que l'on peut en donner : même dans les cas les plus simples, des ambiguïtés et des contradictions peuvent surgir (voir la figure 5). Enfin, il est souvent tellement facile de calculer de telles images, que le risque peut être grand de confondre esthétisme et valeur scientifique : une belle représentation n'est point nécessairement bonne (voir la figure 6), alors que, bien souvent, ce critère d'harmonie est utilisé pour juger une théorie. Malgré cela, il ne faudrait pas négliger l'apport de l'Art à la Science. En effet, il est des codes culturels définis au cours des siècles passés ; ceux-ci doivent être respectés ici sous peine, dans le cas contraire, de produire des visualisations qui soient en contradiction avec nos mécanismes perceptifs. A titre d'exemple, une couleur dite froide (respectivement chaude) est en général associée à des valeurs numériques faibles (respectivement élevées) et cette convention quasi universelle doit ici s'appliquer.

Une fois avertis de ces dangers, les scientifiques et les ingénieurs, ont à leur disposition un nouvel instrument dont les implications épistémologiques auront au moins l'importance qu'en a eu la lunette de Galilée en son temps. Tout ceci débouche sur le concept d'Expérimentation Virtuelle [07]. Cette derniere, complémentaire de l'Expérimentation Réelle [08], consiste donc, tant dans les domaines scientifique qu'industriel, à faire des expériences non point sur un système réel [09], mais sur son modèle mathématique (voir l'encadré 2) et à interagir avec ce dernier par l'intermédiaire d'images de synthèse. Alors, en restant dans le cadre de légalité des lois de la nature, tout nous est permis, et par exemple de créer les univers utiles à nos recherches (voir les figure 1 et 7).

Bien évidemment de nombreuses questions surgissent de cette approche. D'une part, la science et, en particulier, les mathématiques ont-elles droit à ces images ? Et d'ailleurs sont-elles utiles ? Le scientifique ne peut-il se contenter de la seule pensée verbale et bannir alors toute aide visuelle ? Un élément de réponse à cette interrogation est donné par Albert Einstein dans une lettre qu'il ecrivit à Jacques Hadamard : "les mots et le langage, écrits ou parlés, ne semblent pas jouer le moindre rôle dans le mécanisme de ma pensée. Les entités psychiques qui servent d'éléments à la pensée sont certains signes ou des images plus ou moins claires qui peuvent à volonté être reproduits et combinés". Il convient de se souvenir que pendant plusieurs décennies, un large mouvement d'abstraction s'est imposé mais que, l'apparition de nouvelles techniques aidant (ordinateur et synthèse d'image en particulier), nous assistons aujourd'hui à un retour en force de la pensée visuelle. Bien évidemment tout extrémisme est dangereux, ici comme ailleurs ; il ne faudrait pas qu'un mouvement inverse se déclenche et que le je pense donc je suis se transforme en un je calcule et je visualise donc je suis... A titre d'exemple, rappelons que la géométrie fractale a très certainement pris l'essor qu'elle connait actuellement grâce à l'image, mais que, malgré cela, il n'est jamais de certitudes visuelles et que les conjectures qui peuvent être formulées à partir d'une représentation doivent se voir confirmées ou infirmées par un théorème ! L'image doit donc être vue ici simplement comme un levier intellectuel stimulant et entrainant plus loin l'imagination du chercheur, rendant ainsi toute sa noblesse au sens de la vision. D'autre part, ces univers créés dans nos ordinateurs ont-ils le statut ontologique de nouvelles réalités ? Ces "univers-jouets" avec leurs lois calquées sur celles de la nature, ou bien avec d'autres sur lesquelles il nous faut expérimenter, ne sont-ils pas aussi réels que celui que nous n'appréhendons finalement que par les modèles neuronaux créés par nos sens au cours des âges ? Enfin, ces images de science, si elles créent bien souvent la surprise chez ceux qui en ont un besoin immédiat et professionnel, interpellent fréquemment la sensibilité du profane et de l'artiste, signe certain d'un contenu beaucoup plus riche que les apparences ne le laisseraient parfois supposer. Ne sont-elles point alors à entendre comme un lieu de convergence entre l'Art et la Science, ou tout reste encore à voir et à decouvrir ?



  • [01] -Les techniques relatives à l'image numérique peuvent être regroupées en trois catégories distinctes : la synthèse (consistant à calculer des représentations visuelles à partir d'un modèle donné), le traitement (permettant la manipulation et la transformation, tout à la fois d'images calculées et d'images numérisées) et enfin la transmission (assurant le transport et la diffusion).
  • [02] -Les exemples historiques de telles découvertes sont nombreux ; rappelons quelques uns des plus célèbres :
  • [03] -Le modèle mathématique d'un système, qu'il est sensé décrire, contient des équations reliant entre elles les différentes grandeurs caractéristiques (par exemple des coordonnées), des conditions initiales (donnant certaines valeurs à l'instant 0) et enfin des conditions aux limites (précisant, par exemple, ce qui se passe aux frontières du domaine à l'intérieur duquel se fait l'étude).
  • [04] -La précision est exprimée en nombre de bits memorisés et manipulés lors des calculs. Aujourd'hui, le monde scientifique utilise majoritairement les représentations sur 64 bits.
  • [05] -"The subjectivity of computers", Jean-François COLONNA, Technical Correspondence, Communications of the ACM, volume 36, numéro 8, page 15-18, 08/1993.
  • [06] -La propriété d'associativité d'un opérateur x, la multiplication par exemple, signifie que pour trois éléments quelconques A, B et C, l'égalité (AxB)xC=Ax(BxC) est toujours vérifiée.
  • [07] -"Images du Virtuel", Jean-François COLONNA, Addison-Wesley France, Paris, 1994.
  • [08] -Le qualificatif réel étant ici utilisé dans son sens le plus intuitif et loin de tout débat sur la notion de Réalité.
  • [09] -Cela étant sricto sensu de plus en plus difficile ; par exemple, quel physicien a déjà touché une particule élementaire ?




    • Encadre 1 : A titre d'exemple de modèle, examinons brièvement le problème dit des N corps. Etant donné N objets massiques, mais supposés ponctuels, il s'agit d'étudier leurs interactions gravitationnelles à partir de certaines conditions initiales définies à l'instant 0 par l'ensemble des coordonnées et des vitesses. Cette étude doit donc nous fournir pour tout instant futur les positions et les vitesses de chacun de ces corps. Les équations du problème, dans le cadre de la mécanique newtonienne, peuvent être écrites facilement par un élève de terminale S ; mais est-il aisé d'aller ensuite plus avant ? Grâce à Johannes Kepler (Astronomia Nova, 1609) et à sir Isaac Newton (Philosophiae Naturalis Principia Mathematica, 1687) nous savons que pour N égal à 2, l'un des deux corps décrit une ellipse dont l'un des foyers est le second d'entre eux. Mais pour les valeurs de N supérieures à 2, que se passe-t-il ? Pour la réponse à cette question, il a fallu attendre deux cents ans avec les travaux de Henri Poincaré (Les méthodes nouvelles de la mécanique céleste, 1892-1899) ; ce dernier a montré que, bien que les équations soient "simples" comme nous l'avons noté précédemment, ce problème n'avait pas de solution. Ainsi, nous sommes incapables d'écrire des formules exactes qui nous donneraient les informations recherchées (voir la figure 1).


    Encadre 2 : Pour mettre en œuvre le concept d'Expérimentation Virtuelle, il nous faut construire un système informatique approprié. Il peut aujourd'hui reposer sur le concept de méta-ordinateur, assemblage logique (mais non physique) de machines de calcul, de stockage, de visualisation et d'interaction (pouvant utiliser, en particulier, les techniques dites de Réalité Virtuelle), mais aussi d'appareils de mesure (par exemple, le télescope spatial Hubble). Ces différentes composantes n'ont pas besoin d'être physiquement proches l'une de l'autre ; bien au contraire, elles peuvent être réparties sur la planète entière, constituant ainsi des machines, elles-aussi virtuelles, d'une puissance phénoménale. Cette ubiquité électronique est aujourd'hui rendue possible par les réseaux informatiques, dont le plus connu et le plus universel est actuellement Internet ; les lecteurs sont invités à se connecter au serveur A VIRTUAL SPACE-TIME TRAVEL MACHINE qui présente de multiples applications opérationnelles de l'Expérimentation Virtuelle, ainsi que de nombreuses explications complémentaires à cet article. Son nom, A Virtual Space-Time Travel Machine (une machine virtuelle à voyager dans l'espace-temps), a été choisi afin de résumer en une seule expression les possibilités de certains outils de la Science contemporaine...



    Figure 1 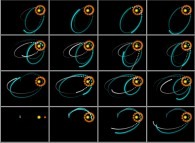: Intégration du problème des N corps avec N=4 pour les conditions initiales suivantes (données en unités MKSA) :

    C1={0,0,0}, V1={0,0,0}, M1=1030,
    C2={26.1010,0,0}, V2={0,-133.102,0}, M2=1028,
    C3={-8.1011,0,0}, V3={0,5.103,0}, M3=2.1027,
    C4={-8.1011,5.1010,0}, V4={-960,5.103,0}, M4=735.1020


    (ou Ck, Vk et Mk représentent respectivement les coordonnées, la vitesse et la masse du corps numéro k).
    Elles sont visualisées en bas et à gauche, alors que le dernier instant du calcul apparait en haut et à droite. Le second corps est proche du premier (l'étoile) et a été choisi très lourd afin qu'il perturbe fortement les trajectoires des troisième et quatrième corps, lorsqu'ils se "frôlent". Ces images montrent qu'alors les trajectoires obtenues sont loin d'être elliptiques et même périodiques.


    Figure 2 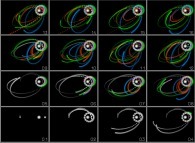: Intégration du problème des N corps avec les mêmes conditions initiales et les mêmes conventions que celles utilisées pour la figure 1. Le même programme C est alors exécuté sur trois ordinateurs (le Rouge, le Vert et le Bleu) qui, bien que compatibles, produisent des résultats incompatibles. D'ou vient alors la différence de comportement ? Elle provient en fait des compilateurs utilisés ; ces programmes sont destinés à traduire les instructions de haut-niveau en opérations élémentaires qui, seules, sont exécutables par les circuits de calcul. Des instructions du type AxBxC seront traduites comme (AxB)xC par certains d'entre eux, et par Ax(BxC) par les autres. La perte de la propriété d'associativité fera ensuite le reste, les erreurs d'arrondi étant différentes d'une machine à l'autre pour une même étape de calcul. Celles-ci, au cours du temps, s'amplifieront et finiront par produire des divergences catastrophiques, ce que ces images montrent mieux que tout discours sur le sujet.


    Figure 3 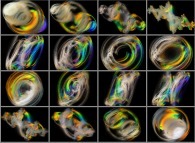: La visualisation d'un ensemble de Julia calculé dans le corps des Quaternions présente des difficultés considérables. Il n'est pas question de représenter directement ses quatre dimensions, puisque nous évoluons dans un espace aux apparences tridimensionnelles. Un artifice doit donc être utilisé : dans ce cas précis, seules sont visualisées seize sections tridimensionnelles obtenues au cours d'une rotation de 2 pi autour de l'un de ses axes. Cette opération, difficile à imaginer, peut être mieux comprise en l'appliquant à un objet de notre espace physique : prenons, par exemple, un cylindre que nous représenterions par une coupe effectuée à l'aide d'un plan arbitraire. Si nous observons l'image de celle-ci alors que le cylindre est en rotation, nous verrons une figure géométrique se déformer et présenter alternativement l'apparence d'un rectangle et d'une ellipse. C'est ce qui est montré ici, le cylindre étant remplacé par un objet fractal à quatre dimensions, et le plan par un hyperplan tridimensionnel...


    Figure 4 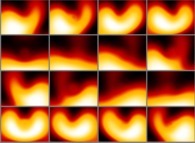: l'hydrogène, le plus simple des atomes, bien qu'il soit parfaitement connu dans le cadre de la Mécanique Quantique, peut encore nous révéler bien des choses. Cette séquence de seize images représente l'évolution au cours du temps, dans certaines conditions qu'il n'est pas utile de préciser ici, de la densité de probabilité de présence de l'électron dans l'espace physique. Celle-ci est codée à l'aide de la luminance de chacun des points de l'image : plus un point est lumineux, plus l'électron a de chance de se trouver sur la ligne de visée joignant l'œil de l'observateur à ce point. Ces images sont extraites d'animations réalisées en collaboration avec Jean-Louis Basdevant pour le cours de Mécanique Quantique qu'il enseigne à l'Ecole Polytechnique.


    Figure 5 : La visualisation d'un tableau de nombres pourrait être considérée, naïvement, comme une opération élémentaire et bien maitrisée depuis de nombreuses décennies. En effet, la géographie ou la météorologie font appel à des couleurs pour représenter des altitudes, des températures ou encore des pressions. Malheureusement, cette simplicité n'est qu'apparente : ces quatre images nous montrent le même ensemble bidimensionnel de nombres, la seule différence demeurant dans le code des couleurs utilisées. En effet, pour obtenir ce type de représentation, il suffit d'associer aux nombres (ou plus généralement à des plages de valeurs numériques) des couleurs (en appelant aussi couleur, par abus de langage, le noir, les gris et le blanc) ; par exemple, il sera décidé arbitrairement de représenter par du rouge les points associés à des valeurs numériques comprises entre 1.37 et 3.62. De cet arbitraire naissent les difficultés ici présentées. De toute évidence, la perception varie fortement d'une image à l'autre, les conclusions possibles sur l'unique tableau de nombres sous-jacent pouvant même être en contradiction les unes avec les autres ! Une sémiologie de la Visualisation Scientifique reste à créer ; elle serait un lieu de rencontre privilégié entre les artistes et les scientifiques.


    Figure 6 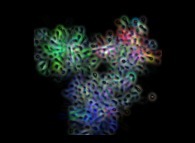: Quelle valeur attribuer à une image dite scientifique ? En plus des erreurs involontaires, inhérentes aux processus de calcul (revoir la figure 2) et de visualisation (revoir la figure 5), il peut être tentant de présenter des images à l'apparence scientifique, mais dont le calcul n'utilise pas les théories qu'elles sont destinées à illustrer. Ainsi, cette image (ainsi que ses semblables maintes fois utilisées), est sensée montrer un nucléon (proton ou neutron) dans le cadre du modèle de l'interaction forte. Malheureusement, la théorie n'est pas suffisante, aujourd'hui, pour rendre compte, tout au moins en des temps de calcul raisonnables, du phénomène dit de confinement. C'est pourquoi, de nombreux artifices durent être implémentés afin de reproduire visuellement celui-ci ; ils représentent environ 80% du programme nécessaire à ces calculs et ne correspondent à aucune réalité physique. De telles pratiques ne sont acceptables que dans un contexte pédagogique, ou l'image n'est plus un intermédiaire entre le chercheur et son modèle, mais simplement un support de communication.


    Figure 7 : La géométrie fractale permet de rendre compte des irrégularités et de la rugosité de nombreux objets et phénomènes naturels. Ce paysage et tout ce qu'il contient (montagnes, nuages,..., exception faite du Soleil levant), sont entièrement calculés à l'aide de quelques grands principes et par exemple celui d'autosimilarité qui nous révèle qu'ici le tout est identique aux parties, à un facteur d'échelle près. Cette image n'est qu'un instant figé à l'intérieur d'une séquence évolutive présentant le lever du jour.


    Copyright © Jean-François COLONNA, 1999-2024.
    Copyright © France Telecom R&D and CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 1999-2024.