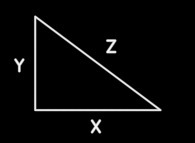
De PYTHAGORE (-VIe siècle) à SIR ANDREW WILES (1994), en passant par DIOPHANTE d'ALEXANDRIE (IIIe siècle), CLAUDE GASPARD BACHET de MEZIRIAC et PIERRE de FERMAT (XVIIe siècle) :

Les équations diophantiennes. L'équation :

                     2    2    2
                    X  + Y  = Z

a une infinité de solutions entières {X,Y,Z} et, par exemple, la plus fameuse d'entre-elles :

                     2    2    2
                    3  + 4  = 5

ou encore :

                     2     2     2
                    5  + 12  = 13

                     2    2     2
                    6  + 8  = 10

                     2     2     2
                    8  + 15  = 17

                     2     2     2
                    9  + 12  = 15

                      2     2     2
                    12  + 16  = 20

                    (...)

Le grand "théorème" de Fermat. L'équation :

                     n    n    n
                    X  + Y  = Z     {X,Y,Z,n} ∈ N     X.Y.Z # 0

n'a pas de solutions entières {X,Y,Z} pour n=0 et n>2.

Le chemin parcouru peut être plus enrichissant que la destination elle-même.

Des applications a posteriori : Courbes elliptiques (conjecture Shimura-Taniyama-Weil démontrée en grande partie par Andrew Wiles) et cryptographie,...

[RETOUR]

www.lactamme.polytechnique.fr