Golden Triangles and Plane non Periodical Penrose Tilings
CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[Real Numbers don't exist in Computers and Floating Point Computations aren't safe. [Les Nombres Réels n'existent pas dans les Ordinateurs et les Calculs Flottants ne sont pas sûrs.]]
[Please, visit A Virtual Machine for Exploring Space-Time and Beyond, the place where you can find more than 10.000 pictures and animations between Art and Science]
(CMAP28 WWW site: this page was created on 05/08/2012 and last updated on 10/03/2024 17:08:28 -CEST-)
[en français/in french]
Keywords: Golden Ratio, Nombre d'or, Golden Rectangle, Rectangle d'or, Golden Triangle, Triangle d'or, Plane Non Periodical Tiling, Pavage Non Périodique du Plan, Penrose Tiling, Pavage de Penrose.
The Golden Ratio (phi) is a very famous number as well known as pi. It is the positive solution of the second degree equation:
2
x = x + 1
and has the value:
___
1 + \/ 5
phi = ----------- ~ 1.6180339887498949
2
The Golden Rectangle is a rectangle whose edge ratio is equal to phi.
It is known as being the most pleasant rectangle to watch and appears white in the following picture:
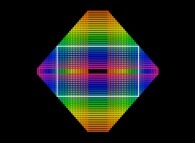
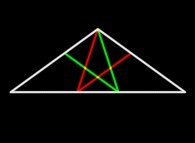
It is possible to define two Golden Triangles (dubbed Flat et Slim respectively).
They are isosceles and their edge ratios are equal to phi and 1/phi respectively.
It is worth noting that they can be subdivided using two different symetrical ways
in a certain number of smaller triangles of the same nature:
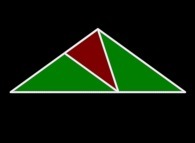
Flat
 =
= 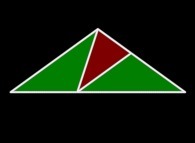 +
+ 
Slim

 =
=  +
+ 
This subdivision process can be repeated again and again at smaller and smaller scales.
It gives birth to a non periodical tiling of the plane (inside the first triangle, the bigger one) in particular
when using a random choice between the red subdivision and the green one.
Here is an example:

With a more complex choice between the two subdivisions, one can associate systematically two triangles of the same kind:

Then, erasing the common edge inside each pair of the preceding triangles one obtains a non periodical tiling
of the plane as devised by Roger Penrose:




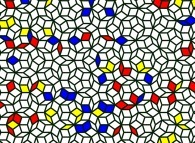





At last, one can "play" with these elements:

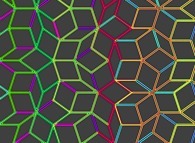










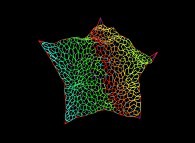








Copyright © Jean-François COLONNA, 2012-2024.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2012-2024.



 =
=  +
+ 

 =
=  +
+ 































