A propos des décimales de 'pi'
(ou comment montrer ce qui n'est pas ?)
CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[Real Numbers don't exist in Computers and Floating Point Computations aren't safe. [Les Nombres Réels n'existent pas dans les Ordinateurs et les Calculs Flottants ne sont pas sûrs.]]
[N'oubliez pas de visiter Une Machine Virtuelle à Explorer l'Espace-Temps et au-delà où vous trouverez plus de 10.000 images et animations à la frontière de l'Art et de la Science]
(Site WWW CMAP28 : cette page a été créée le 21/08/2020 et mise à jour le 16/01/2026 15:00:39 -CET-)
Mots-Clefs : pi.
La constante universelle 'pi' est un nombre transcendant (comme quasiment tous les nombres réels...)
et sa définition contient une infinité de décimales dont
aujourd'hui -en 2026- 62.800 milliards sont connues [01].
La répartition de ces décimales est aléatoire et il est conjecturé (ce qui est vérifié -approximativement-
sur les décimales actuellement connues) qu'il y a autant de 0, que de 1,...,
que de 9. Mais aussi, autant de 00, que de 01,..., que de 99. Mais aussi, autant
de 000, que de 001,..., que de 999,... et ce ad infinitum :
'pi' serait un nombre univers.
On devrait donc y trouver n'importe quel nombre entier : or tout peut
être numérisé, donc TOUT se trouverait dans les décimales de 'pi' (mais c'est vrai aussi
pour tous les nombres réels dits normaux...) : ainsi, à condition d'aller suffisamment
loin on serait sûr d'y trouver la biographie complète de l'auteur, mais aussi toutes ses variantes
(par exemple celle qui relate sa naissance une micro-seconde plus tôt...) [02].
Cette image 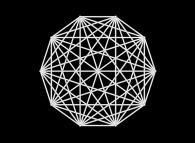 fut réalisée il y a quelques années suite à la publication dans la revue Sciences et Avenir
d'une visualisation des décimales de 'pi' révélant des structures inattendues et extraordinaires !
Ces décimales étant aléatoires, cela ne se pouvait pas et mon image fut destinée à révèler la "supercherie".
fut réalisée il y a quelques années suite à la publication dans la revue Sciences et Avenir
d'une visualisation des décimales de 'pi' révélant des structures inattendues et extraordinaires !
Ces décimales étant aléatoires, cela ne se pouvait pas et mon image fut destinée à révèler la "supercherie".
Mais comment cette image  , elle aussi très structurée, est-elle calculee ?
Sur un cercle
, elle aussi très structurée, est-elle calculee ?
Sur un cercle 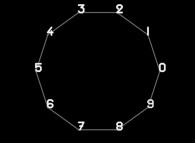 (matérialisé par un décagone) les 10 chiffres
{0,1,2,3,4,5,6,7,8,9}
sont disposés de façon régulière.
(matérialisé par un décagone) les 10 chiffres
{0,1,2,3,4,5,6,7,8,9}
sont disposés de façon régulière.
Ainsi que le montre l'image 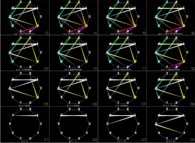 , la première décimale de 'pi' ('1') est marquée sur le cercle,
puis, le point correpondant à la seconde décimale ('4') est joint au premier point (en bas et à gauche).
Les décimales suivantes sont récupérées ensuite les unes après les autres et les points correspondants sur le cercle joints dans le même ordre.
Sur cette image qui ne montre donc que les dix-sept premières décimales il n'apparait aucune symétrie, aucune régularité (ce qui est logique et attendu...).
, la première décimale de 'pi' ('1') est marquée sur le cercle,
puis, le point correpondant à la seconde décimale ('4') est joint au premier point (en bas et à gauche).
Les décimales suivantes sont récupérées ensuite les unes après les autres et les points correspondants sur le cercle joints dans le même ordre.
Sur cette image qui ne montre donc que les dix-sept premières décimales il n'apparait aucune symétrie, aucune régularité (ce qui est logique et attendu...).
Alors, pourquoi l' image  montre-t-elle une structure aussi symétrique ?
Cela vient évidemment de la normalité conjecturée des décimales : s'il y a bien
autant de 00, que de 01,..., que de 99, à condition d'utiliser suffisamment de décimales
(1000 dans cette image -en fait 850 seraient suffisantes-), on est sûr de joindre tout point à tout autre point au moins une fois : d'où la symétrie parfaite !
montre-t-elle une structure aussi symétrique ?
Cela vient évidemment de la normalité conjecturée des décimales : s'il y a bien
autant de 00, que de 01,..., que de 99, à condition d'utiliser suffisamment de décimales
(1000 dans cette image -en fait 850 seraient suffisantes-), on est sûr de joindre tout point à tout autre point au moins une fois : d'où la symétrie parfaite !
Pour montrer que ces symétries ne sont que pures illusions, le cercle (une courbe bidimensionnelle) fut remplacé
par une hélice portée par un cylindre,
hélice (une courbe tridimensionnelle) sur laquelle sont marqués cette fois-ci une
"infinité" de points étiquettés {1,2,3,4,5,6,7,8,9,0} périodiquement 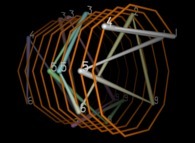 (l'étiquetage commence à 1 qui est la première décimale de 'pi').
Ces points sont ensuite joints les uns après les autres, dans l'ordre des décimales comme précédemment.
Et là, évidemment, les "merveilleuses" symétries disparaissent
(l'étiquetage commence à 1 qui est la première décimale de 'pi').
Ces points sont ensuite joints les uns après les autres, dans l'ordre des décimales comme précédemment.
Et là, évidemment, les "merveilleuses" symétries disparaissent  !
!
Quelques visualisations bi- et tri-dimensionnelles des décimales de 'pi' plus pertinentes !
[01]
- Le 14/03/2019, à l'occasion du pi-day, Google a annoncé que Emma Harula Iwao, à l'aide du logiciel y-cruncher,
avait battu le record du nombre de décimales de 'pi' en en calculant 31.415.926.535.897 (on reconnaitra dans ce nombre les treize premières...).
Puis le 29/01/2020, Timothy Mullican, à l'aide du même logiciel, entrait lui aussi dans l'Histoire du calcul de 'pi' avec 50.000 milliards de décimales
Au mois d'août 2021, la Haute Ecole des Sciences Appliquées des Grisons (HES) en Suisse a annoncé avoir calculé 62.800 milliards de décimales.
Le 09/06/2022 Google a annoncé que de nouveau Emma Harula Iwao, toujours à l'aide du logiciel y-cruncher,
avait battu ce record en en calculant 100.000 milliards sur le Google Cloud...
On notera que c'est en fait à Alexander J. Yee, l'auteur de y-cruncher, que revient le mérite de ces différents records !
Malgré tout, la plus belle performance dans ce domaine reste celle de Fabrice Bellard qui, en 2009, avait calculé 2.700 milliards de décimales sur un "simple" PC.
A suivre...
[Voir les 100.000 premières décimales de pi]
[02]
- Cette remarque n'a évidemment aucun intérêt pratique, si ce n'est d'évoquer la
Bibliothèque de Babel de Jorge Luis Borges...
Copyright © Jean-François COLONNA, 2020-2026.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2020-2026.
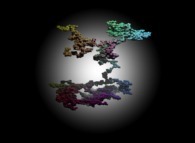
 fut réalisée il y a quelques années suite à la publication dans la revue Sciences et Avenir
d'une visualisation des décimales de 'pi' révélant des structures inattendues et extraordinaires !
Ces décimales étant aléatoires, cela ne se pouvait pas et mon image fut destinée à révèler la "supercherie".
fut réalisée il y a quelques années suite à la publication dans la revue Sciences et Avenir
d'une visualisation des décimales de 'pi' révélant des structures inattendues et extraordinaires !
Ces décimales étant aléatoires, cela ne se pouvait pas et mon image fut destinée à révèler la "supercherie".
 (matérialisé par un décagone) les 10 chiffres
{0,1,2,3,4,5,6,7,8,9}
sont disposés de façon régulière.
(matérialisé par un décagone) les 10 chiffres
{0,1,2,3,4,5,6,7,8,9}
sont disposés de façon régulière.
 , la première décimale de 'pi' ('1') est marquée sur le cercle,
puis, le point correpondant à la seconde décimale ('4') est joint au premier point (en bas et à gauche).
Les décimales suivantes sont récupérées ensuite les unes après les autres et les points correspondants sur le cercle joints dans le même ordre.
Sur cette image qui ne montre donc que les dix-sept premières décimales il n'apparait aucune symétrie, aucune régularité (ce qui est logique et attendu...).
, la première décimale de 'pi' ('1') est marquée sur le cercle,
puis, le point correpondant à la seconde décimale ('4') est joint au premier point (en bas et à gauche).
Les décimales suivantes sont récupérées ensuite les unes après les autres et les points correspondants sur le cercle joints dans le même ordre.
Sur cette image qui ne montre donc que les dix-sept premières décimales il n'apparait aucune symétrie, aucune régularité (ce qui est logique et attendu...).
 (l'étiquetage commence à 1 qui est la première décimale de 'pi').
Ces points sont ensuite joints les uns après les autres, dans l'ordre des décimales comme précédemment.
Et là, évidemment, les "merveilleuses" symétries disparaissent
(l'étiquetage commence à 1 qui est la première décimale de 'pi').
Ces points sont ensuite joints les uns après les autres, dans l'ordre des décimales comme précédemment.
Et là, évidemment, les "merveilleuses" symétries disparaissent  !
!